高中 数学
设数列{an}满足a2+a4=10,点Pn(n,an)对任意的n∈N+ , 都有向量 =(1,2),则数列{an}的前n项和Sn=
=(1,2),则数列{an}的前n项和Sn=
 =(1,2),则数列{an}的前n项和Sn=
=(1,2),则数列{an}的前n项和Sn=
在 的展开式中,
的展开式中, 的系数为.
的系数为.
 的展开式中,
的展开式中, 的系数为.
的系数为.
已知  为椭圆
为椭圆  的右焦点.直线
的右焦点.直线  与椭圆C相交于A,B两点,A,B的中点为P,且直线OP的斜率
与椭圆C相交于A,B两点,A,B的中点为P,且直线OP的斜率  ,则椭圆C的方程为.
,则椭圆C的方程为.
 为椭圆
为椭圆  的右焦点.直线
的右焦点.直线  与椭圆C相交于A,B两点,A,B的中点为P,且直线OP的斜率
与椭圆C相交于A,B两点,A,B的中点为P,且直线OP的斜率  ,则椭圆C的方程为.
,则椭圆C的方程为.
如图所示,扇形所含中心角为  ,弦
,弦  将扇形分成两部分,这两部分各以
将扇形分成两部分,这两部分各以 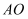 为轴旋转一周,求这两部分旋转所得旋转体的体积
为轴旋转一周,求这两部分旋转所得旋转体的体积 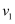 和
和 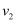 之比.
之比.
 ,弦
,弦  将扇形分成两部分,这两部分各以
将扇形分成两部分,这两部分各以 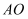 为轴旋转一周,求这两部分旋转所得旋转体的体积
为轴旋转一周,求这两部分旋转所得旋转体的体积 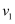 和
和 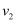 之比.
之比.

如图,直二面角D﹣AB﹣E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
(Ⅰ)求证:AE⊥平面BCE;
(Ⅱ)求二面角B﹣AC﹣E的余弦值;
(Ⅲ)求点D到平面ACE的距离.

已知函数  的最小值为
的最小值为  .
.
 的最小值为
的最小值为  .
.
-
(1) 求
 的值;
的值;
-
(2) 若
 对一切实数
对一切实数  都成立,求实数
都成立,求实数  的取值范围.
的取值范围.
已知0<a<1<b,则下面不等式中一定成立的是( )
A . logab+logba+2>0
B . logab+logba+2<0
C . logab+logba+2≥0
D . logab+logba+2≤0
在等比数列{an}中,若a3a5=10,则a2•a6=.
若实数x,y满足约束条件 , 则
, 则 的最小值为.
的最小值为.
 , 则
, 则 的最小值为.
的最小值为.
已知  ,
,  为平面向量,若
为平面向量,若  与
与  的夹角为
的夹角为  ,
,  与
与  的夹角为
的夹角为  ,则
,则  ( )
( )
 ,
,  为平面向量,若
为平面向量,若  与
与  的夹角为
的夹角为  ,
,  与
与  的夹角为
的夹角为  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在△  中,角
中,角  ,
,  ,
,  所对的边分别为
所对的边分别为  ,
,  ,
,  .现有下列四个条件:①
.现有下列四个条件:①  ,②
,②  ,③
,③  ,④
,④  .
.
 中,角
中,角  ,
,  ,
,  所对的边分别为
所对的边分别为  ,
,  ,
,  .现有下列四个条件:①
.现有下列四个条件:①  ,②
,②  ,③
,③  ,④
,④  .
.
-
(1) ③④两个条件可以同时成立吗?请说明理由;
-
(2) 请在上述四个条件中选择使△
 有解的三个条件,并求出△
有解的三个条件,并求出△  的面积.
的面积.
直线  截圆x2+y2=4所得的弦长是( )
截圆x2+y2=4所得的弦长是( )
 截圆x2+y2=4所得的弦长是( )
截圆x2+y2=4所得的弦长是( )
A . 1
B .  C . 2
D .
C . 2
D . 
 C . 2
D .
C . 2
D . 
不等式  ≤0的解集为( )
≤0的解集为( )
 ≤0的解集为( )
≤0的解集为( )
A . { x|  ≤x≤2}
B . { x|
≤x≤2}
B . { x|  ≤x<2}
C . { x|x>2或 x≤
≤x<2}
C . { x|x>2或 x≤  }
D . { x|x<2}
}
D . { x|x<2}
 ≤x≤2}
B . { x|
≤x≤2}
B . { x|  ≤x<2}
C . { x|x>2或 x≤
≤x<2}
C . { x|x>2或 x≤  }
D . { x|x<2}
}
D . { x|x<2}
已知函数 最小正周期为
最小正周期为 , 则f(x)的图象的一条对称轴的方程是( )
, 则f(x)的图象的一条对称轴的方程是( )
 最小正周期为
最小正周期为 , 则f(x)的图象的一条对称轴的方程是( )
, 则f(x)的图象的一条对称轴的方程是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列说法中,正确的是( )
A . 若 , 则
, 则 B . 函数
B . 函数 与函数
与函数 是同一个函数
C . 设点
是同一个函数
C . 设点 是角
是角 终边上的一点,则
终边上的一点,则 D . 幂函数
D . 幂函数 的图象过点
的图象过点 , 则
, 则
 , 则
, 则 B . 函数
B . 函数 与函数
与函数 是同一个函数
C . 设点
是同一个函数
C . 设点 是角
是角 终边上的一点,则
终边上的一点,则 D . 幂函数
D . 幂函数 的图象过点
的图象过点 , 则
, 则
若某地财政收入x与支出y满足回归方程![]() =
=![]() x+
x+![]() +ei(单位:亿元)(i=1,2,…),其中
+ei(单位:亿元)(i=1,2,…),其中![]() =0.8,
=0.8,![]() =2,|ei|<0.5,如果今年该地区财政收入10亿元,年支出预计不会超过( )
=2,|ei|<0.5,如果今年该地区财政收入10亿元,年支出预计不会超过( )
A.10亿元 B.9亿元
C.10.5亿元 D.9.5亿元
直线![]() 与圆
与圆![]() 交于E,F两点,则
交于E,F两点,则![]() (O是原点)的面积为
(O是原点)的面积为
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
满足条件![]() 的复数
的复数![]() 对应点的轨迹是
对应点的轨迹是
A.直线 B.圆 C.椭圆 D.双曲线
如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()

若函数![]() 是偶函数,则f(x)的递减区间是________.
是偶函数,则f(x)的递减区间是________.
最近更新
- 2010年上海世博会的主题:城市,让生活更美好!城市如同一个符号,走近它,可以领略那些历史的沉淀、感受到时代的变迁。阅读
- 沙漠地区生物种类稀少,造成这一现象的原因是缺乏( ) A. 空气 B. 水分
- 2009年10月29日,我国首台千万亿次超级计算机系统――“天河一号”由国防科学技术大学研制成功。该超级计算机的诞生,使
- 小莉用下图所示装置进行实验,以下叙述错误的是( )A.此装置放在光下几天后,挤压塑料袋,石灰水会变浑浊 B.此装置放
- 做人工呼吸进行口对口吹气时,每分钟吹气的次数应是 A.8~10次 B.16~18次 C.
- —_________have you stayed in Wenzhou? — For about two months
- 如图所示,在高空中有四个小球,在同一位置同时以速率向上、向下、向左、向右被射出,不考虑空气阻力,经过1 s后四个小球在空
- 在Rt△ABC中,∠C=90°,sinA=,则∠A=____ __ .
- 三根长度分别为3cm,7cm,4cm的木棒能围成三角形的事件是( ) A.必然事件 B.不可能事件
- 阅读分析资料和图7,完成下列各题。 抗日战争爆发后,苏联援华物资通过西北陆路运到中国,英美物资通过香港、越南和1938年
- 下列句子中句意明确、没有语病的一句是 A.华航电子有限公司,以人为本利用各种渠道培养和提高在职人员的专业技术水平,取得
- 公元前4世纪时,罗马的某法官接了一个案件:“一个仁慈的贵族罗慕洛,也是罗马一支军队的首领。生前立下遗嘱,希望把自己一半的
- 我国未来将在月球地面上建立月球基地,并在绕月轨道上建造空间站。如图(8)所示,关闭发动机的航天飞机A在月球引力作用下沿椭
- 下列除去杂质的方法不正确的是A. CO2中少量HCl气体:通过饱和NaHCO3溶液后再干燥气体 B. Na2CO3
- 下图是真核细胞内部分能量转换关系图解,请据图回答问题:(1)①过程将光能转换为 ,发生的场
- 温家宝总理曾向媒体和官员引述这样的诗句:“心中为念农桑苦,耳里如闻饥冻声”,“衙斋卧听萧萧竹,疑是民间疾苦声”。从政府机
- 给出以下四个命题,所有真命题的序号为 。 ①从总体中抽取的样本 则回归直线y=bx+a必过点() ②
- 4.没有同源染色体的细胞是:( ) A.有丝分裂前期的细胞 B.次级精母细胞 C.有丝分裂后期的细胞 D初级精母细
- 已知抛物线的函数关系式:(其中是自变量),【小题1】(1)若点在此抛物线上,①求的值;②若,且一次函数的图象与此抛物线没
- 一个质点做方向不变的直线运动,它的加速度的方向与速度的方向相同.但加速度的大小逐渐减小直到零.在此过程中,对质点运动的描



