高中 数学
如图所示,AB是半圆O的直径,VA垂直于半圆O所在的平面,点C是圆周上不同于  的任意一点,
的任意一点, 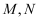 分别为
分别为  的中点,则下列结论正确的是( )
的中点,则下列结论正确的是( )
 的任意一点,
的任意一点, 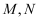 分别为
分别为  的中点,则下列结论正确的是( )
的中点,则下列结论正确的是( ) 
A .  B . 平面
B . 平面  平面
平面  C .
C .  与
与  所成的角为45°
D .
所成的角为45°
D .  平面
平面 
 B . 平面
B . 平面  平面
平面  C .
C .  与
与  所成的角为45°
D .
所成的角为45°
D .  平面
平面 
已知集合  ,则
,则  ( )
( )
 ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知向量 ,
,  , 若
, 若 ∥
∥ , 则
, 则 +
+ =( )
=( )
 ,
,  , 若
, 若 ∥
∥ , 则
, 则 +
+ =( )
=( )
A . (-2,-1)
B . (2,1)
C . (3,-1)
D . (-3,1)
设f(x)=.  ,直线x=0,x=e,y=0,y=1所围成的区域为M,曲线y=f(x)与直线y=1围成的区域为N,在区域M内任取一个点P,则点P在区域N内概率为( )
,直线x=0,x=e,y=0,y=1所围成的区域为M,曲线y=f(x)与直线y=1围成的区域为N,在区域M内任取一个点P,则点P在区域N内概率为( )
 ,直线x=0,x=e,y=0,y=1所围成的区域为M,曲线y=f(x)与直线y=1围成的区域为N,在区域M内任取一个点P,则点P在区域N内概率为( )
,直线x=0,x=e,y=0,y=1所围成的区域为M,曲线y=f(x)与直线y=1围成的区域为N,在区域M内任取一个点P,则点P在区域N内概率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知一个几何体的三视图如图,则该几何体的体积为( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
A是  平面外的一点,E、F分别是BC、AD的中点,
平面外的一点,E、F分别是BC、AD的中点,
 平面外的一点,E、F分别是BC、AD的中点,
平面外的一点,E、F分别是BC、AD的中点, 
-
(1) 求证:直线EF与BD是异面直线;
-
(2) 若
 ,
,  ,求EF与BD所成的角.
,求EF与BD所成的角.
已知直线l1:(k﹣3)x+(4﹣k)y+1=0与l2:(k﹣3)x﹣y+1=0平行,则k的值是.
复数 (其中
(其中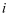 为虚数单位)的值是( )
为虚数单位)的值是( )
 (其中
(其中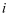 为虚数单位)的值是( )
为虚数单位)的值是( )
A . -1
B . 1
C .  D .
D . 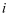
 D .
D . 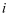
选修4-5:不等式选讲
设不等式  (
(  )的解集为
)的解集为  ,且
,且  ,
,  .
.
-
(1) 求
 的值;
的值;
-
(2) 求函数
 的最小值.
的最小值.
正四棱柱  中,
中,  ,
,  ,O为上底面
,O为上底面  的中心,设正四棱柱
的中心,设正四棱柱  与正四棱锥
与正四棱锥  的侧面积分别为
的侧面积分别为 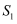 、
、  ,则
,则  .
.
 中,
中,  ,
,  ,O为上底面
,O为上底面  的中心,设正四棱柱
的中心,设正四棱柱  与正四棱锥
与正四棱锥  的侧面积分别为
的侧面积分别为 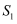 、
、  ,则
,则  .
.
如图所示的直观图的平面图形ABCD是( )

A . 任意梯形
B . 直角梯形
C . 任意四边形
D . 平行四边形
已知函数 .
.
 .
.
-
(1) 求函数
 的单调性;
的单调性;
-
(2) 当
 时,记函数
时,记函数 的最小值为
的最小值为 , 证明:
, 证明: .
.
如图,在四棱锥 中,底面
中,底面 是正方形,平面
是正方形,平面 平面
平面 ,
,  ,
,  , 点
, 点 是棱
是棱 上一点(不包含端点).
上一点(不包含端点).
 中,底面
中,底面 是正方形,平面
是正方形,平面 平面
平面 ,
,  ,
,  , 点
, 点 是棱
是棱 上一点(不包含端点).
上一点(不包含端点).
-
(1) 求证:
 ;
;
-
(2) 若二面角
 的余弦值为
的余弦值为 , 求
, 求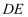 的长度.
的长度.
设等差数列 的前n项和为
的前n项和为 ,若
,若 ,且
,且 ,则当
,则当 取得最大值时,n的值是( )
取得最大值时,n的值是( )
 的前n项和为
的前n项和为 ,若
,若 ,且
,且 ,则当
,则当 取得最大值时,n的值是( )
取得最大值时,n的值是( )
A . 5
B . 6
C . 7
D . 8
若集合  ,
,  ,R表示实数集,则下列选项错误的是( )
,R表示实数集,则下列选项错误的是( )
 ,
,  ,R表示实数集,则下列选项错误的是( )
,R表示实数集,则下列选项错误的是( )
A .  B .
B .  C .
C .  D .
D . 
设连续函数f(x)的定义域为R,已知,若函数f(x)无零点,则f(x)>0或f(x)<0恒成立.
(1)用反证法证明:“若存在实数x0 , 使得f(f(x0))=x0 , 则至少存在一个实数a,使得f(a)=a”;
(2)若f(x)=ex﹣ +x2﹣2cosx﹣mx﹣2,有且仅有一个实数x0 , 使得f(f(x0))=x0 , 求实数m的取值范围.
+x2﹣2cosx﹣mx﹣2,有且仅有一个实数x0 , 使得f(f(x0))=x0 , 求实数m的取值范围.
如图的三视图所示的几何体是( )

A . 六棱台
B . 六棱柱
C . 六棱锥
D . 六边形
已知双曲线C: , 下列对双曲线C的判断正确的是( )
, 下列对双曲线C的判断正确的是( )
 , 下列对双曲线C的判断正确的是( )
, 下列对双曲线C的判断正确的是( )
A . 实轴长是虚轴长的2倍
B . 焦距为8
C . 离心率为 D . 渐近线方程为
D . 渐近线方程为
 D . 渐近线方程为
D . 渐近线方程为
已知△ABC的三个顶点A(m,n)、B(2,1)、C(–2,3).
(1)求BC边所在直线的一般式方程;
(2)BC边上中线AD的方程为2x–3y+c=0,且S△ABC=7,求点A的坐标.
如图是某程序框图的一部分,其算法的逻辑结构为( )

A.顺序结构 B.判断结构
C.条件结构 D.循环结构
最近更新
- 宋代理学的形成是由于() A.道教思想融入儒学 B.佛教思想融入儒学 C.儒家的伦理观出现本质变化 D.吸收佛道的思辨哲
- 设复数z1=a+bi,并且a2+b2=25,z2=3+4i,z1·z2是纯虚数,求z1.
- 已知某一相同温度下:H2(g)+I2(g) 2HI(g)的平衡常数为K1 , 1/2H2(g)+ 1/2I2(g)
- 某城市按以下规定收取每月煤气费,用煤气不超过60立方米,按每立方米0.8元收费;如果超过60立方米,超过部分按每立方米1
- 某同学刚入初中时脊背挺直,三年后发现驼背,其他方面发育正常。造成驼背的原因主要是( ) A.营养不良 B.不经
- 形容其统治为“政启开元,治宏贞观”的是( )A.武则天B.唐太宗C.唐玄宗D.唐高宗
- 所有生物共同具有的一组特征是( )A.呼吸与运动 B.运动与排出废物 C.生长与繁殖 D.需要营
- 下列物质在盛有空气的集气瓶内燃烧,使集气瓶内的压强明显降低的是 A.硫 B.木炭 C.红
- 请你在虚线方框内分别画出物理学中表示平面镜和凸透镜的示意图.
- (本题满分12分) 在高二年级某班学生在数学校本课程选课过程中,已知第一小组与第二小组各有六位同学.每位同学都只选了一个
- 等物质的量的主族金属元素的单质A、B、C,分别与足量的稀盐酸反应,同条件下得氢气的体积依次为VA、VB、VC,已知VB=
- 迎接氢能时代的到来 能源是人类的一个大问题,世界曾经发生过的许多战争,归根结底就是争夺资源,其中能源也是一个很重要
- .“达菲”是瑞士罗氏公司研制的有效治疗人类禽流感的药物.达菲的主要合成原料是我国盛产的莽草酸.
- 相同状况下,在容积相同的三个烧瓶内分别充满干燥的NH3.HCl.NO2气体,然后按上述顺序分别用水做喷泉实验。实验结束后
- 2010年1月,国家统计局初步核算,2009年中国国内生产总值33.535万亿元人民币,按可比价格计算,比上年增长8.7
- (2011·聊城)如图所示,将一根导体棒ab的两端用细导线与灵敏电流计组成一个闭合电路,并用绝缘细线悬挂起来放在U形磁铁
- 民主与专制的主要区别在于( ) A.是否实现了多数人的统治 B.是否具有专政职能 C.广大人民是否真正享有管理国家
- 下列选项中没有错别字的一项是(3分)A.不惮 龟裂 泄秘 志同道和 B.缂丝 臼齿 乳酪
- (08太原市第一次测评)在基因诊断技术中,所用DNA探针必须存在一定的放射性同位索,其作用是 A.为形成杂交DNA
- 【小题1】2+-4【小题2】.



