高中 数学
从装有2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的两个事件是( )
A . 至少有一个是白球与都是白球
B . 至少有一个是白球与至少有一个是红球
C . 至少有一个是白球与都是红球
D . 恰有一个是白球与恰有两个是白球
已知由甲、乙两位男生和丙、丁两位女生组成的四人冲关小组,参加由安徽卫视推出的大型户外竞技类活动《男生女生向前冲》,活动共有四关,设男生闯过一至四关的概率依次是  ,女生闯过一至四关的概率依次是
,女生闯过一至四关的概率依次是  .
.
 ,女生闯过一至四关的概率依次是
,女生闯过一至四关的概率依次是  .
.
-
(1) 求男生闯过四关的概率;
-
(2) 设ε表示四人冲关小组闯过四关的人数,求随机变量ɛ的分布列和期望.
已知数列  的各项均为正整数,对于任意n∈N* , 都有
的各项均为正整数,对于任意n∈N* , 都有  成立,且
成立,且  .
.
 的各项均为正整数,对于任意n∈N* , 都有
的各项均为正整数,对于任意n∈N* , 都有  成立,且
成立,且  .
.-
(1) 求
 ,
,  的值;
的值;
-
(2) 猜想数列
 的通项公式,并给出证明.
的通项公式,并给出证明.
设  分别为双曲线
分别为双曲线  的左,右焦点,过点
的左,右焦点,过点  的直线l与C的一条渐近线交于点P,若
的直线l与C的一条渐近线交于点P,若  轴,且点
轴,且点  到l的距离为2a,则C的离心率为( )
到l的距离为2a,则C的离心率为( )
 分别为双曲线
分别为双曲线  的左,右焦点,过点
的左,右焦点,过点  的直线l与C的一条渐近线交于点P,若
的直线l与C的一条渐近线交于点P,若  轴,且点
轴,且点  到l的距离为2a,则C的离心率为( )
到l的距离为2a,则C的离心率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知抛物线C:y2=2px(p>0),焦点为F,过F的所有弦中,最短弦长为4.
-
(1) 求p的值;
-
(2) 在抛物线C上有两点A,B,过A,B分别作C的切线,两条切线交于点Q,连接QF,AF,BF,求证:|QF|2=|AF|·|BF|.
已知函数  ,函数
,函数  的图象可由
的图象可由 
 的图象经过怎样的平移和伸缩变换得到( )
的图象经过怎样的平移和伸缩变换得到( )
 ,函数
,函数  的图象可由
的图象可由 
 的图象经过怎样的平移和伸缩变换得到( )
的图象经过怎样的平移和伸缩变换得到( )
A . 先将横坐标变为原来两倍,纵坐标不变,再向左平移  个单位
B . 先将横坐标变为原来一半,纵坐标不变,再向左平移
个单位
B . 先将横坐标变为原来一半,纵坐标不变,再向左平移  个单位
C . 先向左平移
个单位
C . 先向左平移  个单位,再将横坐标变为原来的一半,纵坐标不变
D . 先向左平移
个单位,再将横坐标变为原来的一半,纵坐标不变
D . 先向左平移  个单位,再将横坐标变为原来的两倍,纵坐标不变
个单位,再将横坐标变为原来的两倍,纵坐标不变
 个单位
B . 先将横坐标变为原来一半,纵坐标不变,再向左平移
个单位
B . 先将横坐标变为原来一半,纵坐标不变,再向左平移  个单位
C . 先向左平移
个单位
C . 先向左平移  个单位,再将横坐标变为原来的一半,纵坐标不变
D . 先向左平移
个单位,再将横坐标变为原来的一半,纵坐标不变
D . 先向左平移  个单位,再将横坐标变为原来的两倍,纵坐标不变
个单位,再将横坐标变为原来的两倍,纵坐标不变
已知平面向量 ,
,  ,
,  ,
,  .
.
 ,
,  ,
,  ,
,  .
.
-
(1) 求
 ;
;
-
(2) 若
 , 求实数k的值.
, 求实数k的值.
观察下面频率等高条形图,其中两个分类变量C之间关系最强的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若 , 则
, 则 取得最大值时,
取得最大值时,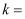 ( )
( )
 , 则
, 则 取得最大值时,
取得最大值时,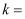 ( )
( )
A . 4或5
B . 5或6
C . 10
D . 5
某三棱锥的三视图如图所示,则该三棱锥的体积是( ).
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
从单词“equation”中选取5个不同的字母排成一排,含有“qu”(其中“qu”相连且顺序不变)概率为( )
A .  B .
B . 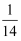 C .
C .  D .
D . 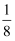
 B .
B . 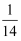 C .
C .  D .
D . 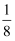
用红、黄、蓝三种颜色去涂图中标号为1,2…9的9个小正方形,使得任意相邻(有公共边)的小正方形所涂
颜色都不相同,且标号为“3,5,7”的小正方形涂相同的颜色,则符合条件的所有涂法共有( )种
1 | 2 | 3 |
4 | 5 | 6 |
7 | 8 | 9 |
A . 18
B . 36
C . 72
D . 108
如图,四棱锥P﹣ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点,F是PC的中点.
(Ⅰ)求证:面PDE⊥面PAB;
(Ⅱ)求证:BF∥面PDE.

设  ,命题若
,命题若  ,则方程
,则方程  有实根的逆否命题是( )
有实根的逆否命题是( )
 ,命题若
,命题若  ,则方程
,则方程  有实根的逆否命题是( )
有实根的逆否命题是( )
A . 若方程  有实根,则
有实根,则  B . 若方程
B . 若方程  有实根,则
有实根,则  C . 若方程
C . 若方程  没有实根,则
没有实根,则  D . 若方程
D . 若方程  没有实根,则
没有实根,则 
 有实根,则
有实根,则  B . 若方程
B . 若方程  有实根,则
有实根,则  C . 若方程
C . 若方程  没有实根,则
没有实根,则  D . 若方程
D . 若方程  没有实根,则
没有实根,则 
关于函数 下列说法正确的是( )
下列说法正确的是( )
 下列说法正确的是( )
下列说法正确的是( )
A . 是周期函数,周期为 B . 关于直线
B . 关于直线 对称
C . 在
对称
C . 在 上最大值为
上最大值为 D . 在
D . 在 上是单调递增的
上是单调递增的
 B . 关于直线
B . 关于直线 对称
C . 在
对称
C . 在 上最大值为
上最大值为 D . 在
D . 在 上是单调递增的
上是单调递增的
设  为等差数列
为等差数列  的前
的前  项和,若
项和,若  ,公差
,公差  ,
,  ,则
,则  ( )
( )
 为等差数列
为等差数列  的前
的前  项和,若
项和,若  ,公差
,公差  ,
,  ,则
,则  ( )
( )
A . 4
B . 5
C . 6
D . 7
已知函数![]() 的反函数
的反函数![]() 的图象过点
的图象过点![]() ,且函数
,且函数![]() 为单调递减函数.
为单调递减函数.
(1)求![]() 的解析式;
的解析式;
(2)求满足![]() 的x的取值范围.
的x的取值范围.
已知函数y=![]() .
.
(1)求定义域;(2)判断奇偶性;
(3)已知该函数在第一象限的图象如图所示,试补全图象,并由图象确定单调区间.

已知![]() 则
则![]() 等于( )
等于( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
下列角中终边与330°相同的角是
A.30° B.-630° C.630° D.-30°
最近更新
- 用括号内所给单词的适当形式填空。 1.Hehas been _________(die)for two years. W
- 下列句子中,加点的词语使用正确的一句是 A.一年前在北京一家意大利餐馆偶尔与米卢结识的意大利人胡里奥,不曾想后来成为了米
- 已知△ABC的顶点B、C在椭圆+y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是(
- 某基态原子的第六电子层只有2个电子,则该原子的第五层中电子数为( ) A.8个 B.8个或18个
- 两条平行的铁轨上匀速行驶着甲、乙两列火车。某时刻两列火车正好交汇,甲车上的一名乘客从一侧车窗看到田野上的树木向北运动,
- 板间距为d的平等板电容器所带电荷量为Q时,两极板间电势差为U1,板间场强为E1.现将电容器所带电荷量变为2Q,板间距变为
- 国家为实现其统治,都要采取一定的政体。现代国家民主政体的共同特征是 ( ) A.议会制 B.总统制
- Which picture shows that the man is walking past the police
- 消费对生产具有巨大的反作用。下列能直接提高消费对经济增长的贡献率的措施是() ①对农民实行粮食最低保护价 ②提高居民最低
- 依次填入下面一段话横线处的词语,最恰当的一组是()。 八股是古代的一种文体,在封建时代用于科举考试。它必须“代圣人立言”
- 在草原上人工种草,为了防止鸟把草籽吃掉,用网把实验区罩上,后来发现,草的叶子几乎被虫吃光而没有加罩的草地反而生产良好,造
- 第三部分 阅读理解(共20小题;每小题2分,满分40分) 第一节 阅读下列短文,从每题所给的四个选项(A、B、C和D
- 温家宝总理在十一届全国人大三次会议上所作政府工作报告中提出,“创造条件让人民批评政府、监督政府”,引起了广泛共鸣。这样做
- —It shouldn't be so difficult to solve the problem if we all
- 若P(2,-1)为圆(x-1)2+y2=25的弦AB的中点,则直线AB的方程为( ) A.2x+y-3=0
- 将足量CO2通入KOH和Ca(OH)2的混合稀溶液中,生成沉淀的物质的量(n)和通入 CO2体积(y)的关系正确的是
- 目前,全球人口总数已超过70亿,人口过多、人口增长过快带来的问题有( ) ①就业困难 ②饥饿贫困 ③住房
- 如图甲,在线圈中通入电流后,在上产生感应电流随时间变化规律如图乙所示,则通入线圈中的电流随时间变化图线是下图中的哪一个?
- 图一材料二:“欧洲已变成一只‘火药桶’,只等一粒火星将它引爆。”于1916年2月发动的这场战役历时十个月,是典型的阵地战
- 下列词语中加点字的读音完全正确的一项是 A. 恐吓(hè) 霉菌(jǔn) 剔除(tī) 深恶



