高中 数学
函数f(x)=2x+3x﹣7的零点所在的区间为(k,k+1),则k=.
设函数  =[
=[  ]
]  .
.
 =[
=[  ]
]  .
.
-
(1) 若曲线
 在点(1,
在点(1,  )处的切线与
)处的切线与  轴平行,求
轴平行,求  ;
;
-
(2) 若
 在
在 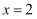 处取得极小值,求
处取得极小值,求  的取值范围.
的取值范围.
在正方体ABCD-A1B1C1D1中,E是C1D1的中点,则异面直线DE与AC所成角的余弦值为( )
A . 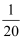 B .
B . 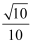 C .
C .  D .
D . 
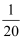 B .
B . 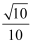 C .
C .  D .
D . 
已知函数f(x)=  ,在(﹣∞,+∞)上是减函数,则实数a的取值范围为( )
,在(﹣∞,+∞)上是减函数,则实数a的取值范围为( )
 ,在(﹣∞,+∞)上是减函数,则实数a的取值范围为( )
,在(﹣∞,+∞)上是减函数,则实数a的取值范围为( )
A . (2,3)
B . [2,3)
C . (1,3)
D . [1,3]
如图所示,  是等腰直角三角形,且
是等腰直角三角形,且  ,E为BC边上的中点,
,E为BC边上的中点, 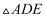 与
与  为等边三角形,点M是线段AB与线段DE的交点,点N是线段
为等边三角形,点M是线段AB与线段DE的交点,点N是线段  与线段EF的交点,若往
与线段EF的交点,若往  中任意投掷一点,该点落在图中阴影区域内的概率为
中任意投掷一点,该点落在图中阴影区域内的概率为 
 参考数据:
参考数据:  ,
, 
 是等腰直角三角形,且
是等腰直角三角形,且  ,E为BC边上的中点,
,E为BC边上的中点, 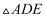 与
与  为等边三角形,点M是线段AB与线段DE的交点,点N是线段
为等边三角形,点M是线段AB与线段DE的交点,点N是线段  与线段EF的交点,若往
与线段EF的交点,若往  中任意投掷一点,该点落在图中阴影区域内的概率为
中任意投掷一点,该点落在图中阴影区域内的概率为 
 参考数据:
参考数据:  ,
, 

A .  B .
B .  C .
C .  D .
D . 
边长为2正方形ABCD,把△ACD沿AC折起至△ACD′,且平面ACD′⊥平面ABC,则三棱锥D′—ABC外接球表面积为( )
A .  B . 2
B . 2  C . 4
C . 4  D . 8
D . 8 
 B . 2
B . 2  C . 4
C . 4  D . 8
D . 8 
已知  为双曲线
为双曲线  :
:  (
(  ,
,  )左支上一点,
)左支上一点,  ,
,  分别为C的左、右焦点,N为虚轴的一个端点,若
分别为C的左、右焦点,N为虚轴的一个端点,若  的最小值为
的最小值为  ,则C的离心率为( )
,则C的离心率为( )
 为双曲线
为双曲线  :
:  (
(  ,
,  )左支上一点,
)左支上一点,  ,
,  分别为C的左、右焦点,N为虚轴的一个端点,若
分别为C的左、右焦点,N为虚轴的一个端点,若  的最小值为
的最小值为  ,则C的离心率为( )
,则C的离心率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数f(x)=ax2﹣  (1)=1.
(1)=1.
 (1)=1.
(1)=1.
-
(1) 求f(x)的解析式;
-
(2) 求f(x)在(1,2)处的切线方程.
在下列区间中,使函数  存在零点的是( )
存在零点的是( )
 存在零点的是( )
存在零点的是( )
A . (0,1)
B . (1,2)
C . (2,e)
D . (3,4)
已知函数f(x)=logax+x﹣b(a>0,且a≠1).当2<a<3<b<4时,函数f(x)的零点x0∈(n,n+1),n∈N* , 求n的值.
已知直线  与直线
与直线  平行,则直线
平行,则直线  ,
,  之间的距离为.
之间的距离为.
 与直线
与直线  平行,则直线
平行,则直线  ,
,  之间的距离为.
之间的距离为.
若“  x<3”是“0≤x≤m”的充分不必要条件,则实数m的取值范围是.
x<3”是“0≤x≤m”的充分不必要条件,则实数m的取值范围是.
 x<3”是“0≤x≤m”的充分不必要条件,则实数m的取值范围是.
x<3”是“0≤x≤m”的充分不必要条件,则实数m的取值范围是.
已知函数 , 在定义域上有两个极值点
, 在定义域上有两个极值点 .
.
 , 在定义域上有两个极值点
, 在定义域上有两个极值点 .
.
-
(1) 求实数a的取值范围;
-
(2) 求证:

对任意实数x,若不等式4x﹣m•2x+1>0恒成立,则实数m的取值范围是( )
A . m<2
B . ﹣2<m<2
C . m≤2
D . ﹣2≤m≤2
数学家华罗庚倡导的“0.618优选法”在各领域都应用广泛,0.618就是黄金分割比  的近似值,黄金分割比还可以表示成
的近似值,黄金分割比还可以表示成  ,则
,则  .
.
 的近似值,黄金分割比还可以表示成
的近似值,黄金分割比还可以表示成  ,则
,则  .
.
 如图,
如图,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
已知集合![]() 则下列式子表示正确的个数为 ( )
则下列式子表示正确的个数为 ( )
![]() ①
①![]() ; ②
; ②![]() ; ③
; ③ ![]() ;④
;④![]() .
.
A.1 B.2 C.3 D.4
一组数据的方差为s2,将这组数据中的每一个数都乘以2所得到的一组新数据的方差为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
若集合![]() 为自然数集,则下列选项正确的是( )
为自然数集,则下列选项正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
在 中,
中, ,其面积为3,设点
,其面积为3,设点 在
在 内,且满足
内,且满足
 ,则
,则 __________.
__________.
最近更新
- 北宋史学家司马光说:才者,德之资也;德者,才之帅也。这一观点( ) A割裂了知识文化修养与思想道德修养的关系B认为“
- 下列加点成语使用恰当的一项是( ) A.两个分别多年的好友谁也不会想到会在这个大都市里戏剧般地萍水相逢,于是激动地热
- 关于物态变化,下列说法正确的是( ) A.雪的形成,属于凝固现象 B.露的形成,属于熔化现象 C.
- 试求至少有一个负根的充要条件.
- 有关非洲的叙述,正确的是() A.非洲是比较晚被人类发现的陆地,故现在经济还比较落后 B.欧洲殖民主义者入侵非洲,最初从
- 11.卢梭说:“设计一种人类的集合体,以用集体力量来保障每一个加盟的个体和他的财产,在这一集体中,个体虽然和整体联系在
- 图是我国海拔3800千米某内陆湖泊的水位变化情况。据此回答下列各题:湖泊水位变化的主要原因是:( )高#考¥资@源
- 配制硫酸亚铁溶液所用的蒸馏水应预先煮沸,以除去溶解在水中的氧气
- -Don’t be late for the meeting this afternoon! -_______A. No
- 阅读下面的宋词,完成下面的题目。 破阵子·为陈同甫赋壮词以寄之 辛弃疾 醉里挑灯看剑,梦回吹角连营。八百里分麾下炙,五十
- 下列离子方程式书写正确的是 ( ) A.过量的CO2通入Ca(ClO)2溶液中 2ClO-+CO2+H
- 【四川省成都市】12.初中三年,语文书是陪伴我们成长的伙伴,请根据要求完成相关题目。 ⑴下面是《成都商报》有关2013年
- 澳大利亚的古老动物中,属卵生哺乳动物的是 ( ) A.考拉 B.鸭嘴兽 C.袋鼠 D.鸸鹋
- 下列不属于中共一大内容的是 A.通过了第一个党纲 B.确立了党的中心任务是领导工人运动 C.确立了党在民主革命时期的任务
- All of us know fibre is hard________. A. to digest
- 物体甲、乙原来静止于光滑水平面上.从t=0时刻开始,甲沿水平面做直线运动,速度随时间变化如图甲;乙受到如图乙所示的水平拉
- 下列各组稀溶液,不用其他试剂或试纸,仅利用溶液间的相互反应,就可以将它们区别开的是 A.硝酸钾 硫酸钠 氯化钙
- 下列哪项措施是为了提高农作物的光合作用效率 ( ) A.松土排涝
- 阅读理解Airline Flight numberDestination Departure time Gate Air
- 请认真阅读下列短文,并根据所读内容在文章后表格中的空格里填人最恰当的单词。 注意:每空格1个单词。 Quality af



