高中 数学
已知直线  ,直线
,直线  ..
..
 ,直线
,直线  ..
..
-
(1) 求直线
 与直线
与直线  的交点
的交点  的坐标,并求出过点
的坐标,并求出过点  与原点距离最大的直线方程;
与原点距离最大的直线方程;
-
(2) 过点
 的直线分别与
的直线分别与  轴的正半轴和
轴的正半轴和  轴的正半轴交于点
轴的正半轴交于点  ,
,  两点,且
两点,且  (
(  为坐标原点),求直线
为坐标原点),求直线  的方程...
的方程...
某班有学生60人,将这60名学生随机编号为1﹣60号,用系统抽样的方法从中抽出4名学生,已知3号、33号、48号学生在样本中,则样本中另一个学生的编号为( )
A . 28
B . 23
C . 18
D . 13
下列函数相等的是( )
A . 函数 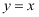 与函数
与函数  B . 函数
B . 函数  与函数
与函数  C . 函数
C . 函数  与函数
与函数 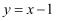 D . 函数
D . 函数  与函数
与函数 
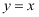 与函数
与函数  B . 函数
B . 函数  与函数
与函数  C . 函数
C . 函数  与函数
与函数 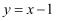 D . 函数
D . 函数  与函数
与函数 
某电子产品公司前四年的年宣传费x(单位:千万元)与年销售量y(单位:百万部)的数据如下表所示:
x(单位:千万元) | 1 | 2 | 3 | 4 |
y(单位:百万部) | 3 | 5 | 6 | 9 |
可以求y关于x的线性回归方程为  =1.9x+1.
=1.9x+1.
参考公式:回归方程  =
=  x+
x+  中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
 =
=  ,
,  =
=  ﹣
﹣  .
.
-
(1) 该公司下一年准备投入10千万元的宣传费,根据所求得的回归方程预测下一年的销售量m:
-
(2) 根据下表所示五个散点数据,求出y关于x的线性回归方程
 =
=  x+
x+  .
. x(单位:千万元)
1
2
3
4
10
y(单位:百万部)
3
5
6
9
m
并利用小二乘法的原理说明
 =
=  x+
x+  与
与  =1.9x+1的关系.
=1.9x+1的关系.
在 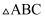 中,
中,  ,若
,若  ,
,  ,
,  ,且
,且  ,
,  ,则有( )
,则有( )
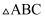 中,
中,  ,若
,若  ,
,  ,
,  ,且
,且  ,
,  ,则有( )
,则有( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数  ,则
,则  的值为
的值为
 ,则
,则  的值为
的值为
已知函数  =
=  当2<a<3<b<4时,函数
当2<a<3<b<4时,函数  的零点
的零点  .
.
 =
=  当2<a<3<b<4时,函数
当2<a<3<b<4时,函数  的零点
的零点  .
.
已知数列 为等差数列,
为等差数列, ,
,  , 以
, 以 表示
表示 的前n项和,则使得
的前n项和,则使得 达到最小值的
达到最小值的 是( )
是( )
 为等差数列,
为等差数列, ,
,  , 以
, 以 表示
表示 的前n项和,则使得
的前n项和,则使得 达到最小值的
达到最小值的 是( )
是( )
A . 37和38
B . 38
C . 37
D . 36和37
若集合  中有且仅有一个元素,则k的值为.
中有且仅有一个元素,则k的值为.
 中有且仅有一个元素,则k的值为.
中有且仅有一个元素,则k的值为.
试写出  的展开式中系数最大的项.
的展开式中系数最大的项.
 的展开式中系数最大的项.
的展开式中系数最大的项.
已知函数  在区间
在区间  上单调递增,则实数
上单调递增,则实数  的可能值为( )
的可能值为( )
 在区间
在区间  上单调递增,则实数
上单调递增,则实数  的可能值为( )
的可能值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列关于向量 ,
,  ,
,  的运算,一定成立的有( )
的运算,一定成立的有( )
 ,
,  ,
,  的运算,一定成立的有( )
的运算,一定成立的有( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
高二某班班会选出包含甲、乙、丙的5名学生发言,要求甲、乙两人的发言顺序必须相邻,而乙、丙两人的发言顺序不能相邻,那么不同的发言顺序共有( )
A . 48种
B . 36种
C . 24种
D . 12种
某医院医疗就诊流程如图所示,则病人到医院就诊至少需要的步骤是( )

A . 6个
B . 7个
C . 8个
D . 9个
设全集为R,集合  ,则
,则  ( )
( )
 ,则
,则  ( )
( )
A .  B . {1}
C .
B . {1}
C .  D .
D . 
 B . {1}
C .
B . {1}
C .  D .
D . 
已知三棱锥 的各顶点都在一个半径为
的各顶点都在一个半径为 的球面上, 球心
的球面上, 球心 在
在 上,
上, 底面
底面 ,
,  , 则球的体积与三棱锥体积之比是( )
, 则球的体积与三棱锥体积之比是( )
 的各顶点都在一个半径为
的各顶点都在一个半径为 的球面上, 球心
的球面上, 球心 在
在 上,
上, 底面
底面 ,
,  , 则球的体积与三棱锥体积之比是( )
, 则球的体积与三棱锥体积之比是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设f(x)为定义于(﹣∞,+∞)上的偶函数,且f(x)在[0,+∞)上为增函数,则f(﹣2)、f(﹣π)、f(3)的大小顺序是( )
A . f(﹣π)>f(3)>f(﹣2)
B . f(﹣π)>f(﹣2)>f(3)
C . f(﹣π)<f(3)<f(﹣2)
D . f(﹣π)<f(﹣2)<f(3)
一个由八个面围成的几何体的三视图如图所示,它的表面积为( )
A .  B . 8
C . 12
D .
B . 8
C . 12
D . 
 B . 8
C . 12
D .
B . 8
C . 12
D . 
α是第四象限角,![]() ,则sinα等于( )
,则sinα等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
已知双曲线![]() 的一个焦点在圆
的一个焦点在圆![]() 上,则双曲线的渐近线方程为( )
上,则双曲线的渐近线方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
最近更新
- 已知式子 是关于x的二次多项式,且二次项系数为b,数轴上A、B两点所对应的数分别是a和b. (1)则a=____,b
- 下图反映的是一定时期某种商品供求量(Q轴)随价格(P轴)变化的情况。其中,曲线D为需求曲线,曲线S为供给曲线,两曲线交
- One afternoon last summer I was driving along on my way home
- . .---Did you enjoy the movie? ---Sure, it is___________a
- 1952年,西欧六国成立欧洲煤钢共同体,正式启动了欧洲一体化进程。经过半个多世纪的发展,到2004年5月1日,欧盟已经成
- 地球上种类和数量最多的动物是( ) A.软体动物 B.昆虫
- There was a time when I thought my dad I didn’t 36 him
- 设的值是( )A. B.
- 己知25℃时,Ksp(AgCl) =1.8×10-10,Ksp(AgBr) =5.4×10-13,Ksp(AgI) =8
- 下列关于电功、电功率和焦耳定律的说法中正确的是( )A.电功率越大,电流做功越快,电路中产生的焦耳热一定越多
- 阅读下列短文,根据短文内容,从短文后各题所给的A、B、C、D四个选项中,选择最佳选项。Victoria Middle S
- 下列用品的主要成分及其用途,对应不正确的是
- 下图所示是一个电池、电阻R与平行板电容器组成的串联电路,在增大电容器两极板间距离的过程中( ) A.电阻R中没有电
- He ______ be at home, because the light in his room is on.A.
- 右图为空气成分示意图(按体积计算),其中“a”代表的是 A.氧气 B.氮气 C.二氧化碳
- 下列各句中,没有语病的一句是( ) A.2008年,美国联邦政府拿出了5亿美元让低收入家庭“拥有自住房”的特别
- 几乎整个由大洋构成的板块是 A.亚欧板块 B.印度洋板块 C.太平洋板
- Try as you , he won’t listen to your advice on the potential
- 设m、n是平面α外的一条直线,给出三个论断:①m∥n;②m∥α;③n∥α.以其中两个为条件,余下的一个为结论,构成三个命
- 分解因式:



