高中 数学
已知  ,
,  满足约束条件
满足约束条件  .当且仅当
.当且仅当 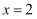 ,
,  时,
时,  取得最小值,其中
取得最小值,其中  ,
,  ,则
,则  的最大值为.
的最大值为.
 ,
,  满足约束条件
满足约束条件  .当且仅当
.当且仅当 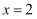 ,
,  时,
时,  取得最小值,其中
取得最小值,其中  ,
,  ,则
,则  的最大值为.
的最大值为.
若复数 ,
,  (
( 为虚数单位),则
为虚数单位),则 在复平面内对应的点位于第象限.
在复平面内对应的点位于第象限.
 ,
,  (
( 为虚数单位),则
为虚数单位),则 在复平面内对应的点位于第象限.
在复平面内对应的点位于第象限.
已知向量 =(
=( , 1),
, 1), =(m,1).若向量
=(m,1).若向量 ,
,  的夹角为
的夹角为 , 则实数m=( )
, 则实数m=( )
 =(
=( , 1),
, 1), =(m,1).若向量
=(m,1).若向量 ,
,  的夹角为
的夹角为 , 则实数m=( )
, 则实数m=( )
A . - B .
B .  C . ﹣
C . ﹣ 或0
D . 2
或0
D . 2
 B .
B .  C . ﹣
C . ﹣ 或0
D . 2
或0
D . 2
在 中b=4,B=45
中b=4,B=45 , C=75
, C=75 , 则a=( )
, 则a=( )
 中b=4,B=45
中b=4,B=45 , C=75
, C=75 , 则a=( )
, 则a=( )
A .  B .
B . 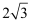 C .
C .  D .
D . 
 B .
B . 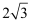 C .
C .  D .
D . 
如图,在四棱锥  中,
中,  底面
底面  ,
,  ,
,  ,
,  ,
, 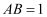 ,点
,点  为棱
为棱  的中点.
的中点.
 中,
中,  底面
底面  ,
,  ,
,  ,
,  ,
, 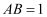 ,点
,点  为棱
为棱  的中点.
的中点. 
-
(1) 证明

-
(2) 求直线
 与平面
与平面  所成角的正弦值;
所成角的正弦值;
-
(3) 若
 为棱
为棱  上一点,满足
上一点,满足  ,求平面
,求平面  与平面
与平面  夹角的余弦值.
夹角的余弦值.
在  的展开式中,含
的展开式中,含  的项的二项式系数为
的项的二项式系数为
 的展开式中,含
的展开式中,含  的项的二项式系数为
的项的二项式系数为
数列{an}和{bn}均为等差数列,a1+b1=3,a3+b3=7,则a10+b10的值为( )
A . 20
B . 21
C . 22
D . 23
设向量 与
与 的夹角为
的夹角为 , 定义
, 定义 与
与 的“外积”:
的“外积”: 是一个向量,它的模
是一个向量,它的模 , 若
, 若 ,
,  , 则|
, 则| |=( )
|=( )
 与
与 的夹角为
的夹角为 , 定义
, 定义 与
与 的“外积”:
的“外积”: 是一个向量,它的模
是一个向量,它的模 , 若
, 若 ,
,  , 则|
, 则| |=( )
|=( )
A .  B .
B . 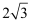 C . 2
D . 4
C . 2
D . 4
 B .
B . 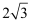 C . 2
D . 4
C . 2
D . 4
在正方体  中,点M在线段
中,点M在线段  上运动,则下列说法正确的是( )
上运动,则下列说法正确的是( )
 中,点M在线段
中,点M在线段  上运动,则下列说法正确的是( )
上运动,则下列说法正确的是( )
A . 直线  平面
平面  B . 直线
B . 直线  与平面
与平面  所成角的正弦值的最大值为
所成角的正弦值的最大值为  C . 异面直线AM与
C . 异面直线AM与  所成角的取值范围是
所成角的取值范围是  D . 三棱锥
D . 三棱锥  的体积为定值
的体积为定值
 平面
平面  B . 直线
B . 直线  与平面
与平面  所成角的正弦值的最大值为
所成角的正弦值的最大值为  C . 异面直线AM与
C . 异面直线AM与  所成角的取值范围是
所成角的取值范围是  D . 三棱锥
D . 三棱锥  的体积为定值
的体积为定值
如图,在四棱柱ABCD﹣A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k,(k>0)

-
(1) 求证:CD⊥平面ADD1A1
-
(2) 若直线AA1与平面AB1C所成角的正弦值为
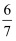 ,求k的值
,求k的值
-
(3) 现将与四棱柱ABCD﹣A1B1C1D1形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为f(k),写出f(k)的解析式.(直接写出答案,不必说明理由)
对任意的实数 ,若
,若 表示不超过
表示不超过 的最大整数,则
的最大整数,则 是
是 的( )
的( )
 ,若
,若 表示不超过
表示不超过 的最大整数,则
的最大整数,则 是
是 的( )
的( )
A . 充分不必要条件
B . 必要不充分条件
C . 充要条件
D . 既不充分也不必要条件
已知函数f(x)=x3+ax2+bx(a、b∈R)的图象过点P(1,2),且在点P处的切线斜率为8.
-
(1) 求a、b的值;
-
(2) 求函数f(x)的单调区间.
已知△ABC的三个内角A,B,C所对的边分别是a,b,c,向量  =(cos B,cos C),
=(cos B,cos C),  =(2a+c,b),且
=(2a+c,b),且  ⊥
⊥  .
.
 =(cos B,cos C),
=(cos B,cos C),  =(2a+c,b),且
=(2a+c,b),且  ⊥
⊥  .
.
-
(1) 求角B的大小;
-
(2) 若b=
 ,求a+c的范围.
,求a+c的范围.
已知{an}是等差数列,{bn}是等比数列,Sn为数列{an}的前n项和,a1=b1=1,且b3S3=36,b2S2=8(n∈N+).
-
(1) 求an和bn;
-
(2) 若an<an+1 , 求数列
 的前n项和Tn .
的前n项和Tn .
已知函数![]() 在R上满足
在R上满足![]() ,则曲线
,则曲线![]() 在点
在点![]() 处的切线方程是( )
处的切线方程是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]() 若函数
若函数![]() (a>0,且a
(a>0,且a![]() 1)有两个零点,则实数a的取值范围是 _
1)有两个零点,则实数a的取值范围是 _
若直线y=x+b与曲线y=3﹣![]() 有公共点,则b的取值范围是 .
有公共点,则b的取值范围是 .
函数f(x)=|x|(![]() -
-![]() )是( )
)是( )
A. 是奇函数又是减函数 B. 是奇函数但不是减函数
C. 是减函数但不是奇函数 D. 不是奇函数也不是减函数
函数![]() 的图象在点
的图象在点![]() 处的切线的倾斜角为
处的切线的倾斜角为
A.0 B.![]() C.1 D.
C.1 D. ![]()
已知![]() ,有如下四个结论:
,有如下四个结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
则正确结论的序号是
A.①③ B.②③ C.①④ D.①④
最近更新
- Phil White hasjust returned from an 18,000 mile, around the
- 设M={x|0≤x≤2},N={y|0≤y≤2},给出下列四个图形,其中能表示从集合M到集合N的函数关系的有()A
- 要想提高电磁振荡的频率,下列办法中可行的是( ) A.线圈中插入铁芯
- 下列关于糖类、蛋白质、油脂的说法中,正确的是 A.它们的组成中都有C、H、O、N等元素 B.在一定条件下,它们都能发生水
- 在盐酸与铁的反应中,盐酸 A. 是氧化剂 B. 是还原剂 C. 不是氧化剂也不是还原剂 D.既是
- —Bob,are you going to study abroad? —Sorry, I’m not _______
- “我们的制度之所以称为民主政治,因为政权是在全体公民手中,而不是在少数人手中。”以上言论出自于古希腊著名的政治家
- 阅读下面的文言文,完成1~4题。 徐有功,名弘敏,避孝敬皇帝讳,以字行,国子博士文远孙也。举明经,累补薄州
- 有人说生活就是妥协的结果,国与国之间的外交也是如此;妥协一定要有底线和原则,一旦突破了底线和违背了原则,就会给国与国之间
- 下列关于物质燃烧现象的表述错误的是 A.木炭在氧气中燃烧,生成黑色固体 B.蜡烛燃烧产生能使石
- 汉字积累——下列词语中加点字读音完全正确的一项是 ( ) A.迤逦(lǐ) 琥珀(pó) 梵
- 百花盛开,阵阵花香,沁人心脾.花香四溢的现象说明( ) A.分子是不断运动的
- 如图,双曲线与直线相交于点M,N,且点M的坐标为(1,3),点N的纵坐标为.根据图象信息可得关于x的方程的解为(
- 两物体组成的系统总动量守恒,这个系统中( )A.一个物体增加的速度等于另一个物体减少的速度B.一物体受的冲量与另
- 中国十七届五中全会于2010年10月18日审议通过了关于制定国民经济和社会发展第十二个五年规划(简称“十二五”规划)的建
- 中国与各民主党派的关系与美国共和党与民主党之间的关系是根本不同的。其不同点在于 A.前者代表无产阶级和劳动人民的利益,后
- 从水分子分解示意图中我们能获得许多信息,其中描述错误的是 A.这是一个化合反应 B.水分解时元素的种类不变 C.氢分子能
- 下列说法正确的是() A.6.02×1023个12C原子数就是阿伏加德罗常数 B.1 mol氧的质量是32 g C.氢原
- 在空间直角坐标系中,,,点在直线上,则 A. B. C. D.
- 读北京市平原区地下水埋藏深度过程线图,完成关于该地区地下水埋藏深度变化特点的表述,正确的是A.降水多的季节地下水埋藏浅B



