高中 数学
已知平面向量 的夹角为
的夹角为 且
且 , 在
, 在 中,
中, , D为BC中点,则
, D为BC中点,则 ( )
( )
 的夹角为
的夹角为 且
且 , 在
, 在 中,
中, , D为BC中点,则
, D为BC中点,则 ( )
( )
A . 2
B . 4
C . 6
D . 8
南宋著名数学家秦九韶在其著作《数书九章》中创用了“三斜求积术”,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上.以小斜幂乘大斜幂减上,余四约之,为实.一为从隅,开平方得积.”翻译一下这段文字,即已知三角形的三边长,可求三角形的面积为  .若
.若  中,内角
中,内角  ,
,  ,
,  所对的边分别为
所对的边分别为  ,
,  ,
,  ,且
,且  ,
,  ,
,  ,则用“三斜求积术”求得
,则用“三斜求积术”求得  的面积为( )
的面积为( )
 .若
.若  中,内角
中,内角  ,
,  ,
,  所对的边分别为
所对的边分别为  ,
,  ,
,  ,且
,且  ,
,  ,
,  ,则用“三斜求积术”求得
,则用“三斜求积术”求得  的面积为( )
的面积为( )
A . 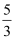 B . 1
C .
B . 1
C .  D .
D . 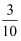
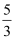 B . 1
C .
B . 1
C .  D .
D . 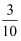
在同一直角坐标系中,函数f(x)=xa(x>0),g(x)=logax的图象可能是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
函数  的零点个数为.
的零点个数为.
 的零点个数为.
的零点个数为.
设a,b是两条不重合的直线,  ,
,  是两个不同的平面.下列四个命题中,正确的是( )
是两个不同的平面.下列四个命题中,正确的是( )
 ,
,  是两个不同的平面.下列四个命题中,正确的是( )
是两个不同的平面.下列四个命题中,正确的是( )
A . 若  ,
,  ,则
,则 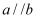 B . 若
B . 若  ,
,  ,则
,则 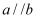 C . 若
C . 若  ,
,  ,则
,则  D . 若
D . 若  ,
,  ,则
,则 
 ,
,  ,则
,则 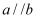 B . 若
B . 若  ,
,  ,则
,则 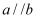 C . 若
C . 若  ,
,  ,则
,则  D . 若
D . 若  ,
,  ,则
,则 
把6张不同的充值卡分给4位同学,每人至少1张,有种分法
已知向量  .若
.若  ,则实数
,则实数  的值为.
的值为.
 .若
.若  ,则实数
,则实数  的值为.
的值为.
定义在 上的偶函数
上的偶函数 满足:对任意
满足:对任意 [0,+∞),且
[0,+∞),且 都有
都有 , 则( )
, 则( )
 上的偶函数
上的偶函数 满足:对任意
满足:对任意 [0,+∞),且
[0,+∞),且 都有
都有 , 则( )
, 则( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知向量 若
若 与
与 平行,则实数x的值是( )
平行,则实数x的值是( )
 若
若 与
与 平行,则实数x的值是( )
平行,则实数x的值是( )
A . -2
B . 0
C . 1
D . 2
某几何体的三视图如图所示,其中圆的半径均为1,则该几何体的体积为( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
函数f(x)=(m2﹣m﹣1)xm是幂函数,且在x∈(0,+∞)上为增函数,则实数m的值是( )
A . 2
B . 3
C . 4
D . 5
在  中,内角
中,内角  ,
,  ,
,  所对的边分别为
所对的边分别为  ,
,  ,
,  .已知
.已知 
 中,内角
中,内角  ,
,  ,
,  所对的边分别为
所对的边分别为  ,
,  ,
,  .已知
.已知 
-
(1) 求角
 的大小;
的大小;
-
(2) 若
 ,求
,求  边上的高的最大值.
边上的高的最大值.
若方程  所表示的曲线为
所表示的曲线为  ,则下列命题正确的是( )
,则下列命题正确的是( )
 所表示的曲线为
所表示的曲线为  ,则下列命题正确的是( )
,则下列命题正确的是( )
A . 若  为椭圆,则
为椭圆,则  B . 若
B . 若  为双曲线,则
为双曲线,则  或
或  C . 曲线
C . 曲线  可能是圆
D . 若
可能是圆
D . 若  为焦点在
为焦点在  轴上的椭圆,则
轴上的椭圆,则 
 为椭圆,则
为椭圆,则  B . 若
B . 若  为双曲线,则
为双曲线,则  或
或  C . 曲线
C . 曲线  可能是圆
D . 若
可能是圆
D . 若  为焦点在
为焦点在  轴上的椭圆,则
轴上的椭圆,则 
已知数列{an}是无穷等比数列,其前n项和是Sn , 若a2+a3=2,a3+a4=1,则limSn的值为.( )
A .  B .
B .  C .
C . 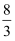 D .
D . 
 B .
B .  C .
C . 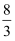 D .
D . 
已知函数  ,则不等式
,则不等式  的解集是.
的解集是.
 ,则不等式
,则不等式  的解集是.
的解集是.
已知函数 的最小值为
的最小值为 , 则
, 则  ( )
( )
 的最小值为
的最小值为 , 则
, 则  ( )
( )
A .  B .
B .  C . e
D .
C . e
D . 
 B .
B .  C . e
D .
C . e
D . 
已知向量![]() ,
,![]() ,且
,且![]() ,求:
,求:
⑴![]() 及
及![]() ;
;
⑵求函数![]() 的最小值。
的最小值。
已知![]() ,
,![]() ,函数
,函数![]() .
.
(1)求函数![]() 的值域;
的值域;
(2)在![]() 中,角
中,角![]() 和边
和边![]() 满足
满足![]() ,求边
,求边![]() .
.
以下命题为真命题的个数是( )
①若直线![]() 平行于平面
平行于平面![]() 内的无数条直线,则直线
内的无数条直线,则直线![]() ;
;
②若直线![]() 在平面
在平面![]() 外,则
外,则![]() ;
;
③若直线![]() ,
,![]() ,则
,则![]() ;
;
④若直线![]() ,
,![]() ,则
,则![]() 平行于平面
平行于平面![]() 内的无数条直线.
内的无数条直线.
A.1个 B.2个
C. 3个 D.4个
如图为某几何体的三视图,则该几何体的表面积为( )

A. B.
B.  C.
C.  D.
D. 

A.
最近更新
- 阅读下面的文言文,完成后面题目。 饮泉亭记 【明】 刘基 昔司马氏①有廉臣焉,曰吴君隐之,出刺广州,过贪泉而饮之,赋诗曰
- 下列试验描述正确的是:可以用本尼迪特试剂与人血液混合,经沸水浴后根据出现的沉淀量来判断血液中葡萄糖的含量 提取鸡血红细胞
- 世纪中叶,普鲁士国王弗里德里希二世在大力加强专制统治的同时,改进司法制度,放松新闻检查,禁止驱逐农民。这反映他受到了哪位
- p{font-size:10.5pt;line-height:150%;margin:0;padding:0;}td{f
- 晋文公入主中原奠定霸业的著名战役是( ) A. 涿鹿大战 B. 城濮大战 C. 长平之战
- 往100mL pH=0的硫酸和硝酸混合液中投入3.84g铜粉,微热使反应充分完成后,生成一氧化氮气体448mL(标准状况
- 分式无意义,则x的值( )A.1B.C.0D.
- 下列句子中加点的成语的使用,不恰当的一句是 (
- 已知某种水果的批发单价与批发量的函数关系如图(1)所示. (1)请说明图中①、②两段函数图象的实际意义.(2)写出批发该
- 近两年来,当股市阳光灿烂时居民的储蓄存款纷纷流入股市,当股市阴雨低迷时,银行存款又急剧增加。这一经济现象说明() ①我国
- 函数f(x)=x3-15x2-33x+6的单调减区间为________.
- 小明今年比去年高了5厘米,这与细胞的 和 有关
- 近年来,建筑装潢装饰材料进入家庭。调查发现,经装修的居室中有装潢装饰材料缓慢释放出的化学物质浓度过高,影响人体健康。这些
- Idon’t doubt _________ our team will win, but I do doubt __
- 比较阅读【甲】【乙】两个文段,完成5—9题。(16分) 【甲】亲贤臣,远小人,此先汉所以兴隆也;亲小人,远贤臣,此后汉所
- 2008年12月31日公布的一份最新统计数据显示,20家全球最大的上市企业所拥有的现金量总额为5700亿美元。位居这份名
- 30. Let Harris play with your toys as well, Clare. You must
- 在甲、乙两个型号相同的量筒内各注入10mL清水,再在各量筒内插入一株形态结构基本相同的芹菜,并将乙量筒内芹菜的叶摘除。然
- We arranged to meet at 8:00, but she never ______. A. turn d
- 小明买了一种“汽泡爽”的冲调饮料。 【饮料说明】 ①主要原料:柠檬酸(C6H8O7)和小苏打(NaHCO3); ②使用说



