高中 数学
已知圆  ,椭圆
,椭圆  的短半轴长等于圆
的短半轴长等于圆  的半径,且过
的半径,且过  右焦点的直线与圆
右焦点的直线与圆  相切于点
相切于点  .
.
 ,椭圆
,椭圆  的短半轴长等于圆
的短半轴长等于圆  的半径,且过
的半径,且过  右焦点的直线与圆
右焦点的直线与圆  相切于点
相切于点  .
.
-
(1) 求椭圆
 的方程;
的方程;
-
(2) 若动直线
 与圆
与圆  相切,且与
相切,且与  相交于
相交于  两点,求点
两点,求点  到弦
到弦  的垂直平分线距离的最大值.
的垂直平分线距离的最大值.
已知全集  ,集合
,集合  ,
,  ,那么
,那么  ( )
( )
 ,集合
,集合  ,
,  ,那么
,那么  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列命题正确的是( )
A . 若ac>bc⇒a>b
B . 若a2>b2⇒a>b
C . 若  D . 若
D . 若 
 D . 若
D . 若 
已知  ,
,  ,则
,则 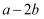 的取值范围是( )
的取值范围是( )
 ,
,  ,则
,则 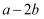 的取值范围是( )
的取值范围是( )
A .  ,
,  B .
B .  C .
C .  D .
D . 
 ,
,  B .
B .  C .
C .  D .
D . 
周长为l的铁丝弯成下部为矩形,上部为半圆形的框架(如图所示),若矩形底边长为2x,求此框架围成图形的面积y关于x的函数解析式为( )

A . y=  ,
,  B . y=
B . y=  C . y=-
C . y=-  x2+lx,
x2+lx,  D . y=-
D . y=-  x2+lx
x2+lx
 ,
,  B . y=
B . y=  C . y=-
C . y=-  x2+lx,
x2+lx,  D . y=-
D . y=-  x2+lx
x2+lx
已知函数f(x)=  的图象上有且仅有四个不同的点关于直线y=﹣1的对称点在y=kx﹣1的图象上,则实数k的取值范围是( )
的图象上有且仅有四个不同的点关于直线y=﹣1的对称点在y=kx﹣1的图象上,则实数k的取值范围是( )
 的图象上有且仅有四个不同的点关于直线y=﹣1的对称点在y=kx﹣1的图象上,则实数k的取值范围是( )
的图象上有且仅有四个不同的点关于直线y=﹣1的对称点在y=kx﹣1的图象上,则实数k的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设全集  ,集合
,集合  ,
,  ,则
,则  ( )
( )
 ,集合
,集合  ,
,  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设函数  ,则
,则  ( )
( )
 ,则
,则  ( )
( )
A . 是偶函数,在  上单调递减
B . 是奇函数,在
上单调递减
B . 是奇函数,在  上单调递增
C . 是偶函数,在
上单调递增
C . 是偶函数,在  上单调递增
D . 是奇函数,在
上单调递增
D . 是奇函数,在  上单调递增
上单调递增
 上单调递减
B . 是奇函数,在
上单调递减
B . 是奇函数,在  上单调递增
C . 是偶函数,在
上单调递增
C . 是偶函数,在  上单调递增
D . 是奇函数,在
上单调递增
D . 是奇函数,在  上单调递增
上单调递增
已知双曲线  ,双曲线
,双曲线  的左、右焦点分别为F1 , F2 , M是双曲线C2的一条渐近线上的点,且OM⊥MF2 , O为坐标原点,若
的左、右焦点分别为F1 , F2 , M是双曲线C2的一条渐近线上的点,且OM⊥MF2 , O为坐标原点,若  ,且双曲线C1 , C2的离心率相同,则双曲线C2的实轴长是( )
,且双曲线C1 , C2的离心率相同,则双曲线C2的实轴长是( )
 ,双曲线
,双曲线  的左、右焦点分别为F1 , F2 , M是双曲线C2的一条渐近线上的点,且OM⊥MF2 , O为坐标原点,若
的左、右焦点分别为F1 , F2 , M是双曲线C2的一条渐近线上的点,且OM⊥MF2 , O为坐标原点,若  ,且双曲线C1 , C2的离心率相同,则双曲线C2的实轴长是( )
,且双曲线C1 , C2的离心率相同,则双曲线C2的实轴长是( )
A . 32
B . 16
C . 8
D . 4
函数  的导函数
的导函数  在
在  上的图象大致为( )
上的图象大致为( )
 的导函数
的导函数  在
在  上的图象大致为( )
上的图象大致为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数  满足
满足  ,当
,当  时,
时,  ,则不等式
,则不等式  的解集为( )
的解集为( )
 满足
满足  ,当
,当  时,
时,  ,则不等式
,则不等式  的解集为( )
的解集为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数f(x)=  ,若使不等式f(x)<
,若使不等式f(x)<  成立,则x的取值范围为.
成立,则x的取值范围为.
 ,若使不等式f(x)<
,若使不等式f(x)<  成立,则x的取值范围为.
成立,则x的取值范围为.
已知菱形  的边长为2,
的边长为2,  ,点
,点  ,
,  分别在边
分别在边  ,
, 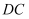 上,
上,  ,
,  ,若
,若  ,则
,则  的值为( )
的值为( )
 的边长为2,
的边长为2,  ,点
,点  ,
,  分别在边
分别在边  ,
, 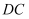 上,
上,  ,
,  ,若
,若  ,则
,则  的值为( )
的值为( )
A . 3
B . 2
C .  D .
D . 
 D .
D . 
从双曲线 的左焦点F引圆
的左焦点F引圆 的切线,切点为T, 延长FT交双曲线右支于点P, O为坐标原点,M为PF 的中点,则
的切线,切点为T, 延长FT交双曲线右支于点P, O为坐标原点,M为PF 的中点,则  与b-a的大小关系为 ( )
与b-a的大小关系为 ( )
A .  B .
B .  C .
C .  D . 不能确定
D . 不能确定
 B .
B .  C .
C .  D . 不能确定
D . 不能确定
如图,已知  =
=  ,
,  =
=  ,
,  =3
=3  ,用
,用  ,
,  表示
表示  ,则
,则  等于( )
等于( )
 =
=  ,
,  =
=  ,
,  =3
=3  ,用
,用  ,
,  表示
表示  ,则
,则  等于( )
等于( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
集合 ,
,  , 则
, 则 ( )
( )
 ,
,  , 则
, 则 ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期.一研究团队统计了某地区1000名患者的相关信息,得到如下表格:
潜伏期(单位:天) |
|
|
|
|
|
|
|
人数 | 50 | 150 | 200 | 300 | 200 | 60 | 40 |
附: , 其中
, 其中 .
.
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
-
(1) 求这1000名患者的潜伏期的样本平均数值
 (同一组中的数据用该组区间的中点值作代表,结果四舍五入为整数);
(同一组中的数据用该组区间的中点值作代表,结果四舍五入为整数);
-
(2) 该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过8天为标准进行分层抽样,从上述1000名患者中抽取200人,得到如下列联表,请将列联表补充完整,并根据列联表判断,能否在犯错误的概率不超过5%的前提下,认为潜伏期与患者年龄有关;
潜伏期
 8天
8天潜伏期
 天
天总计
50岁以上(含50)
100
50岁以下
65
总计
200
-
(3) 以这1000名患者的潜伏期超过8天的频率,代替该地区1名患者潜伏期超过8天的概率,每名患者的潜伏期是否超过8天相互独立.为了深入研究,该研究团队随机调查了20名患者,其中潜伏期超过8天的人数最有可能(即概率最大)是多少?
已知二次函数![]() 对任意实数x不等式
对任意实数x不等式![]() 恒成立,且
恒成立,且![]() ,令
,令![]() .
.
(I)求![]() 的表达式;
的表达式;
(II)若![]() 使
使![]() 成立,求实数m的取值范围;
成立,求实数m的取值范围;
(III)设![]() ,
,![]() ,证明:对
,证明:对![]() ,恒有
,恒有![]()
在![]() 中,已知
中,已知![]() ,那么
,那么![]() 一定是( )
一定是( )
A. 等腰直角三角形 B. 直角三角形
C. 等腰三角形 D. 等边三角形
命题“∀x∈R,x2+1>0”的否定是( )
A.∀x∈R,x2+1<0 B.∀x∈R,x2+1≤0 C.∃x∈R,x2+1≤0 D.∃x∈R,x2+1<0
最近更新
- ―How can we enter that strange house? ―Oh, it’s not difficul
- We have every reason to believe that ______ 2010 World Expo
- 请在下面方框中填上恰当的标点符号。 也许是因为拔何首乌毁了泥墙罢,也许是因为将砖头抛到间壁的梁家去了罢 也许是因为站
- 细嚼馒头,口腔内感觉有甜味,这是由于() A.牙齿咀嚼的缘故 B.舌搅拌的缘故 C.口腔分泌消化酶的缘故 D.与以上
- 下列颜色不属于因化学反应而产生的现象的是 ( ) A.无色试剂瓶中的浓硝酸呈黄色 B.久置的KI溶液呈
- 第16届亚运会组委会举行吉祥物发布仪式。吉祥物取名乐羊羊,形象是运动时尚的五只羊,分别取名“阿祥”、“阿和”、“阿如”、
- 如图所示,倒置的光滑圆锥面内侧,有质量相同的两个小玻璃球A、B,沿锥面在水平面内作匀速圆周运动,关于A、B两球的角速度、
- 用细线将一质量为m、电荷量为q的小球悬挂在天花板下面,设在空中存在沿水平方向的匀强电场,当小球静止时把细线烧断,小球将做
- 西双版纳地区的支柱产业是( )。澳门的支柱产业是( )。
- 新鲜水果、蔬菜、乳制品中富含的维生素C具有明显的抗衰老作用,但易被空气氧化。某课外小组利用碘滴定法测某橙汁中维生素C的含
- 中共中央最近印发《关于培育和践行社会主义核心价值观的意见》,明确把“三个倡导” 确立为社会主义核心价值观的基本内容,并对
- 阅读材料,回答下列问题。 下图所示国家是世界文明古国之一,R河流域是该国文明的重要发祥地,而R河下游为地上河,几乎年年河
- (本小题满分10分) ,且. (1)求实数的值; (2)求在区间上的最大值和最小值.
- 英文单词CHINA是瓷器的意思,读音来自“昌南”的读音,昌南镇即被称为瓷都的景德镇。古代中国的制瓷业特别发达,世界领先,
- Itwas not until she got home Maryrealized she had los
- 小雨从超市买同一包纯碱,其包装说明如图1所示.他称取了11g纯碱样品溶于水中配制成50g溶液,然后向溶液中滴加氯化钙溶液
- The water will be polluted unless some measures _____.
- (本题满分共12分)如图,在中,为边上高,,,沿将翻折,使得,得到几何体。(1)求证:; (2)求与平面成角的正切值。
- 电动机的转动轴分粗细两部分,粗轴半径为R,细轴半径为r,两部分轴上绕有细绳,绳子通过动滑轮,动滑轮下悬挂重物P,绳子及滑
- 甲基丙烯酸甲酯是世界上年产量超过100万吨的高分子单体,旧法合成的反应是:(CH3)2C=O+HCN(CH3)2C(OH












