高中 数学
设  为三个平面,a,b为直线,已知
为三个平面,a,b为直线,已知  ,下列说法正确的是( )
,下列说法正确的是( )
 为三个平面,a,b为直线,已知
为三个平面,a,b为直线,已知  ,下列说法正确的是( )
,下列说法正确的是( )
A . 若  ,则
,则 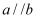 B . 若
B . 若  ,则
,则 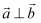 C . 在
C . 在  内存在直线与
内存在直线与  垂直
D . 若
垂直
D . 若  ,则
,则 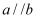
 ,则
,则 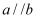 B . 若
B . 若  ,则
,则 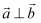 C . 在
C . 在  内存在直线与
内存在直线与  垂直
D . 若
垂直
D . 若  ,则
,则 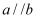
在验证吸烟与否与患肺炎与否有关的统计中,根据计算结果,认为这两件事情无关的可能性不足1%,那么  的一个可能取值为( )
的一个可能取值为( )

A . 6.635
B . 5.024
C . 7.897
D . 3.841
已知函数  的导函数为
的导函数为  ,则
,则  .
.
 的导函数为
的导函数为  ,则
,则  .
.
已知函数  ,函数
,函数  ,其中
,其中  ,
,  是
是  的一个极值点,且
的一个极值点,且  .
.
 ,函数
,函数  ,其中
,其中  ,
,  是
是  的一个极值点,且
的一个极值点,且  .
.
-
(1) 讨论
 的单调性
的单调性
-
(2) 求实数
 和a的值
和a的值
-
(3) 证明

椭圆  的焦距是2,则m的值是( )
的焦距是2,则m的值是( )
 的焦距是2,则m的值是( )
的焦距是2,则m的值是( )
A . 5
B . 5或8
C . 3或5
D . 20
函数y=cosx在区间[﹣π,a]上为增函数,则a的范围是
一个均匀的正四面体的四个面分别写有1,2,3,4四个数字,现随机投掷两次,正四面体底面上的数字分别为x1 , x2 , 记t=  .
.
 .
.
-
(1) 分别求出t取得最大值和最小值时的概率;
-
(2) 求t≥4的概率.
在  中,内角
中,内角  ,
,  ,
,  的对边分别为
的对边分别为  ,
,  ,
,  .若
.若  的面积为
的面积为  ,且
,且  ,
,  ,则
,则  外接圆的面积为( )
外接圆的面积为( )
 中,内角
中,内角  ,
,  ,
,  的对边分别为
的对边分别为  ,
,  ,
,  .若
.若  的面积为
的面积为  ,且
,且  ,
,  ,则
,则  外接圆的面积为( )
外接圆的面积为( )
A . 4π
B . 2π
C . π
D . 

已知定义在  上的函数
上的函数  满足
满足  ,且
,且  在
在  单调递增,对任意的
单调递增,对任意的  ,恒有
,恒有  ,则使不等式
,则使不等式  成立的
成立的  取值范围是.
取值范围是.
 上的函数
上的函数  满足
满足  ,且
,且  在
在  单调递增,对任意的
单调递增,对任意的  ,恒有
,恒有  ,则使不等式
,则使不等式  成立的
成立的  取值范围是.
取值范围是.
某赛季甲、乙两位运动员每场比赛得分的茎叶图如图所示:

-
(1) 从甲、乙两人的这5次成绩中各随机抽取一个,求甲的成绩比乙的成绩高的概率;
-
(2) 试用统计学中的平均数、方差知识对甲、乙两位运动员的测试成绩进行分析.
已知动点P(x,y)与两定点M(﹣1,0),N(1,0)连线的斜率之积等于常数λ(λ≠0).
(I) 求动点P的轨迹C的方程;
(II) 试根据λ的取值情况讨论轨迹C的形状.
为了得到函数  的图象,可将函数
的图象,可将函数  的图象( )
的图象( )
 的图象,可将函数
的图象,可将函数  的图象( )
的图象( )
A . 向左平移  个单位
B . 向右平移
个单位
B . 向右平移  个单位
C . 向左平移
个单位
C . 向左平移  个单位
D . 向右平移
个单位
D . 向右平移  个单位
个单位
 个单位
B . 向右平移
个单位
B . 向右平移  个单位
C . 向左平移
个单位
C . 向左平移  个单位
D . 向右平移
个单位
D . 向右平移  个单位
个单位
已知定义在 上的奇函数
上的奇函数 满足
满足 .当
.当 时,
时, , 则
, 则 ( )
( )
 上的奇函数
上的奇函数 满足
满足 .当
.当 时,
时, , 则
, 则 ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数f(x)=|x﹣2|+|x+1|.
-
(1) 作出函数y=f(x)的图象;
-
(2) 解不等式|x﹣2|+|x+1|≥5.
设命题p:﹣1<log  x<0,q:2x>1,则p是q成立的是( )
x<0,q:2x>1,则p是q成立的是( )
 x<0,q:2x>1,则p是q成立的是( )
x<0,q:2x>1,则p是q成立的是( )
A . 充分不必要条件
B . 必要不充分条件
C . 充分必要条件
D . 既不充分也不必要条件
若![]() ,则
,则![]() _ ________ .
_ ________ .
已知函数![]()
![]() (Ⅰ)当
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的最大值;(Ⅱ)当
的最大值;(Ⅱ)当![]() 时,曲线
时,曲线![]() 在点
在点![]() 处的切线
处的切线![]() 与
与![]() 有且只有一个公共点,求
有且只有一个公共点,求![]() 的值.
的值.
已知![]() ,数列{
,数列{![]() }的前n项和为Sn,数列{bn}的通项公式为
}的前n项和为Sn,数列{bn}的通项公式为![]() =n-8,则
=n-8,则![]() 的最小值为_____.
的最小值为_____.
已知函数![]() 在
在![]() 上单调,且函数
上单调,且函数![]() 的图象关于
的图象关于![]() 对称,若数列
对称,若数列![]() 是公差不为0的等差数列,且
是公差不为0的等差数列,且![]() ,则
,则![]() 的前100项的和为( )
的前100项的和为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
已知函数 (其中
(其中 为常数且
为常数且 )在
)在 处取得极值.
处取得极值.
(1)当 时,求
时,求 的极大值点和极小值点;
的极大值点和极小值点;
(2)若 在
在 上的最大值为1,求
上的最大值为1,求 的值.
的值.
(1)当
(2)若
最近更新
- 与-3互为相反数的是【▲】A.-3 B.3 C.-
- — I was wondering if you could lend me some more money? — So
- 融雪剂可以融化道路上的积雪。某种融雪剂由氯化钠和氯化钙组成,为测定该融雪剂中氯化钙的质量分数,称量2.4 g融雪剂放入烧
- 阅读下列材料,结合所学知识回答问题。和谐社会是指一种美好的社会状态和一种美好的社会理想,即“形成全体人们各尽
- 填表:除去下列物质中混有的杂质(括号内为杂质) 选用试剂分离操作名称苯(苯酚) 溴苯(溴) 甲烷(乙烯)
- 您一定看过《喜羊羊与灰太狼》吧。狼和羊在漫长的生存斗争中都得到进化,根据达尔文的生物进化理论,狼和羊进化是
- 求函数的极值。
- 若黄赤交角变小时,下列说法正确的是() A.热带、寒带范围扩大,温带范围缩小 B.寒带、温带、热带三带分界线的纬度缩小
- 从行政监督体系看,属于行政系统内部监督的中央国家机关是( ) A.中共中央纪律检查委员会
- 以下说法中正确的是 A.一杯热水在打开杯盖后,
- 第二次工业革命时期,开发和利用的相对清洁的新能源是() A.煤炭B.石油C.电力D.原子能
- 将51.2 g Cu完全溶于适量浓硝酸中,收集到氮的氧化物(含NO、N2O4、NO2)的混合物共0.8 mol,这些气体
- This work is ____ for me thanfor you. A. difficult B. most
- 2015年3月29日到4月6日,中国政府分四批从战火纷飞的也门安全撤离了629名中国公民,还协助来自15个国家共279名
- 群落演替在后期的成熟阶段 A 总生产量与生物量的比值最高 B 总生产量、净生产量达到最大C 总生产量大于总呼吸量 D
- 下图表示的是某动物细胞内三种细胞器生物膜结构在某过程前与后的面积变化,那么该过程产生的物质很可能是下列哪一项() A.肠
- 2009年12月1日,被称为“简版”《欧盟宪法条约》的_______正式生效,欧盟在一体化进程中又迈出关键一步。 A.《
- 如图甲是a 、 b 、 c 三种固体物质的溶解度曲线,试回答下列相关问题。 (1)t 1℃ 时, a 、 b 、 c 的
- 下列各句中,没有语病、语意明确的一句是 A.前段时间,部分网民对部分省市GDP数字的真实性提出质疑,引发了人们对部分官员
- 按如图所示的程序计算.若输入x的值为3,则输出的值为 ﹣3 .



