高中 数学
若函数 为奇函数,则a的值为 ( )
为奇函数,则a的值为 ( )
 为奇函数,则a的值为 ( )
为奇函数,则a的值为 ( )
A .  B .
B .  C .
C .  D . 1
D . 1
 B .
B .  C .
C .  D . 1
D . 1
已知向量 ,
,  ,
,  , 若
, 若 , 则实数m的值为( )
, 则实数m的值为( )
 ,
,  ,
,  , 若
, 若 , 则实数m的值为( )
, 则实数m的值为( )
A . 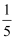 B . -3
C .
B . -3
C .  D .
D . 
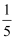 B . -3
C .
B . -3
C .  D .
D . 
在 中, 角
中, 角 、
、 、
、 的对边分别是
的对边分别是 、
、 、
、 , 若
, 若 , 则
, 则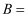 ( )
( )
 中, 角
中, 角 、
、 、
、 的对边分别是
的对边分别是 、
、 、
、 , 若
, 若 , 则
, 则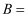 ( )
( )
A . 6
B . 7
C .  D .
D . 
 D .
D . 
下列是关于函数y=f(x),x∈[a,b]的命题中,正确的是( )
A . 若x0∈[a,b]且满足f(x0)=0,则x0是f(x)的一个零点;
B . 若x0是f(x)在[a,b]上的零点,则可用二分法求x0的近似值;
C . 函数f(x)的零点是方程f(x)=0的根,但f(x)=0的根不一定是函数f(x)的零点;
D . 用二分法求方程的根时,得到的都是近似解
设  ,
,  ,
,  ,则
,则  ,
,  ,
,  的大小关系是.(按照从大到小的顺序排列)
的大小关系是.(按照从大到小的顺序排列)
 ,
,  ,
,  ,则
,则  ,
,  ,
,  的大小关系是.(按照从大到小的顺序排列)
的大小关系是.(按照从大到小的顺序排列)
“ 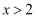 ”是“
”是“  ”的( )
”的( )
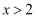 ”是“
”是“  ”的( )
”的( )
A . 必要不充分条件
B . 充分不必要条件
C . 充要条件
D . 既不充分也不必要条件
在  中,角
中,角  ,
,  ,
,  的对边分别为
的对边分别为  ,
,  ,
,  .若
.若  ,且
,且  ,则
,则  .
.
 中,角
中,角  ,
,  ,
,  的对边分别为
的对边分别为  ,
,  ,
,  .若
.若  ,且
,且  ,则
,则  .
.
如图,四棱锥  中,底面
中,底面  为矩形,
为矩形,  是等边三角形,平面
是等边三角形,平面  平面
平面  ,
,  为
为  的中点.
的中点.
 中,底面
中,底面  为矩形,
为矩形,  是等边三角形,平面
是等边三角形,平面  平面
平面  ,
,  为
为  的中点.
的中点. 
-
(1) 求证:
 平面
平面  ;
;
-
(2) 若
 ,
,  ,试问在线段DE上是否存在点Q,使得直线BQ与平面PCD所成角的正弦值为
,试问在线段DE上是否存在点Q,使得直线BQ与平面PCD所成角的正弦值为  ?若存在,求出此时DQ的长;若不存在,请说明理由.
?若存在,求出此时DQ的长;若不存在,请说明理由.
若  ,则
,则  的值为.
的值为.
 ,则
,则  的值为.
的值为.
已知函数  的最大值为3,其中
的最大值为3,其中  .
.
 的最大值为3,其中
的最大值为3,其中  .
.
-
(1) 求实数m的值;
-
(2) 若
 求证:
求证:  .
.
在一次数学测试中,甲、乙、丙、丁四位同学中只有一位同学得了满分,他们四位同学对话如下,甲:我没考满分;乙:丙考了满分;丙:丁考了满分;丁:我没考满分.其中只有一位同学说的是真话,据此,判断考满分的同学是.
设a , b , c都是正数,求证: .
.
 .
.
某医院有内科医生5名,外科医生4名,现要派4名医生参加赈灾医疗队,
-
(1) 一共有多少种选法?
-
(2) 其中某内科医生甲必须参加,某外科医生乙因故不能参加,有几种选法?
-
(3) 内科医生和外科医生都要有人参加,有几种选法?
已知  、
、  、
、 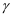 是三个不同的平面,且
是三个不同的平面,且  ,
,  ,则“
,则“  ”是“
”是“  ”的( )
”的( )
 、
、  、
、 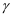 是三个不同的平面,且
是三个不同的平面,且  ,
,  ,则“
,则“  ”是“
”是“  ”的( )
”的( )
A . 充分而不必要条件
B . 必要而不充分条件
C . 充分必要条件
D . 既不充分也不必要条件
设 是公差不为0的等差数列
是公差不为0的等差数列 的前n项和,且
的前n项和,且 成等比数列,则
成等比数列,则 ( )
( )
 是公差不为0的等差数列
是公差不为0的等差数列 的前n项和,且
的前n项和,且 成等比数列,则
成等比数列,则 ( )
( )
A . 4
B . 6
C . 8
D . 10
设矩阵M= 的逆矩阵是M﹣1=
的逆矩阵是M﹣1= , 则a+c的值为 .
, 则a+c的值为 .
 的逆矩阵是M﹣1=
的逆矩阵是M﹣1= , 则a+c的值为 .
, 则a+c的值为 .
已知  ,
,  ,
,  是
是  的导函数,则下列结论正确的是( )
的导函数,则下列结论正确的是( )
 ,
,  ,
,  是
是  的导函数,则下列结论正确的是( )
的导函数,则下列结论正确的是( )
A .  在
在  上单调递增.
B .
上单调递增.
B .  在
在 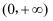 上两个零点
C . 当
上两个零点
C . 当  时,
时,  恒成立,则
恒成立,则  D . 若函数
D . 若函数  只有一个极值点,则实数
只有一个极值点,则实数 
 在
在  上单调递增.
B .
上单调递增.
B .  在
在 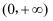 上两个零点
C . 当
上两个零点
C . 当  时,
时,  恒成立,则
恒成立,则  D . 若函数
D . 若函数  只有一个极值点,则实数
只有一个极值点,则实数 
已知锐角三角形![]() 的面积为
的面积为![]() ,
,![]() ,
,![]() ,则角
,则角![]() 的大小为( )
的大小为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5位同学站成一排照相,其中甲与乙必须相邻,且甲不能站在两端的排法总数是( )
A.40 B.36 C.32 D.24
下列四个函数中,具有性质“对任意的实数![]() ,函数
,函数![]() 满足
满足![]() ”的是( )
”的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
最近更新
- 19世纪末,在资本主义相对稳定的环境中,国际工人运动和社会主义呈现哪些新特点?
- 此题要求改正所给短文中的错误。对标有题号的每一行做出判断,每一行均有一处错误。请按下列情况进行改正。 此行多一个词:把多
- Jeff enjoyed ________ reception he received on his return to
- 人体的结构层次是 ( )A.细胞→组织→系统→器官→个体 B.细胞→组织→器官→系统→个体 C.细胞→器
- 设的极小值为,其导函数的图像开口向下且经过点,. (Ⅰ)求的解析式;(Ⅱ)方程有唯一实数解,求的取值范围. (Ⅲ)若对
- Dogs are known for a strong sense of smell. Theirnoses can b
- 如果-3 是分式方程 的增根,则a= ;
- 13.右上图中,X代表的细胞是A.效应T细胞 B.效应B细胞 C.吞噬细胞 D.癌细胞
- 下列关于氧化物的各项叙述正确的是( ) ①酸性氧化物肯定是非金属氧化物 ②碱性氧化物肯定是金属氧化
- -- _____ have you studied English? –For about nine years.
- 2008年9月来,世界经济金融危机日趋严峻,为抵御国际经济环境对我国的不利影响,我国政府出台更加有力的扩大国内需求十项措
- (1-)10的二项展开式中,x的系数与x9的系数之差为: .
- SCR和NSR技术可有效降低柴油发动机在空气过量条件下的NOx排放。 (1)SCR(选择性催化还原)工作原理:①尿素[C
- 已知在酸性条件下有以下反应关系: ①KBrO3能将I-氧化成KIO3,本身被还原为Br2; ②Br2能将I-氧化为I2;
- 已知等差数列{an}满足a2+a4=4,a3+a5=10,则它的前10项的和S10=() A.138, B.13
- 如图4所示,质量为M的木板放在倾角为θ的光滑斜面上,质量为m的人在木板上跑,假如脚与板接触处不打滑.(1)要保持木板相对
- 某种富含乳酸亚铁的口服液可以比较有效地治疗人类缺铁性贫血,这是因为其中的Fe2+进入人体后能() A.调节血液的酸碱平衡
- Before goingoutside in the morning, many of us check a wind
- 从离地H高处自由下落小球a,同时在它正下方H让以速度V0竖直上抛另一小球b,不计空气阻力,有
- __________ full preparations, we decided to put off the meet



