高中 数学
已知双曲线  的右焦点
的右焦点  到其中一条渐近线
到其中一条渐近线  的距离等于
的距离等于  ,则双曲线的离心率为.
,则双曲线的离心率为.
 的右焦点
的右焦点  到其中一条渐近线
到其中一条渐近线  的距离等于
的距离等于  ,则双曲线的离心率为.
,则双曲线的离心率为.
直线3x+4y=b与圆x2+y2﹣2x﹣2y+1=0相切,则b=( )
A . ﹣2或12
B . 2或﹣12
C . ﹣2或﹣12
D . 2或12
若函数f(x)=  (a∈R)是奇函数,则a的值为( )
(a∈R)是奇函数,则a的值为( )
 (a∈R)是奇函数,则a的值为( )
(a∈R)是奇函数,则a的值为( )
A . 1
B . 0
C . -1
D . ±1
函数  的图像大致为( )
的图像大致为( )
 的图像大致为( )
的图像大致为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10  cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(Ⅰ)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(Ⅱ)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.

设等差数列 的前项和为
的前项和为 , 若
, 若 ,
,  , 则
, 则 等于( )
等于( )
 的前项和为
的前项和为 , 若
, 若 ,
,  , 则
, 则 等于( )
等于( )
A . 180
B . 90
C . 72
D . 100
某食品厂为了检测某批袋装食品的质量,从该批食品中抽取了一个容量为100的样本,测量它们的质量(单位:克).根据数据分为  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  七组,其频率分布直方图如图所示.
七组,其频率分布直方图如图所示.
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  七组,其频率分布直方图如图所示.
七组,其频率分布直方图如图所示. 
-
(1) 根据频率分布直方图,估计这批袋装食品质量的中位数.(保留一位小数)
-
(2) 记产品质量在
 内为优等品,每袋可获利5元;产品质量在
内为优等品,每袋可获利5元;产品质量在  内为不合格品,每袋亏损2元;其余的为合格品,每袋可获利3元.若该批食品共有10000袋,以样本的频率代替总体在各组的频率,求该批袋装食品的总利润.
内为不合格品,每袋亏损2元;其余的为合格品,每袋可获利3元.若该批食品共有10000袋,以样本的频率代替总体在各组的频率,求该批袋装食品的总利润.
若logax=2,logbx=3,logcx=6,则log(abc)x=( )
A .  B . 0
C .
B . 0
C .  D . 1
D . 1
 B . 0
C .
B . 0
C .  D . 1
D . 1
已知函数  ,且函数
,且函数  有两个零点,求实数
有两个零点,求实数  的取值范围.
的取值范围.
 ,且函数
,且函数  有两个零点,求实数
有两个零点,求实数  的取值范围.
的取值范围.
函数y=x|x|+px2 , x∈R,下列说法正确的是( )
A . 偶函数
B . 奇函数
C . 不具有奇偶函
D . 奇偶性与p有关
果农采摘水果,采摘下来的水果会慢慢失去新鲜度.已知某种水果失去新鲜度h与其采摘后时间t(天)满足的函数关系式为 . 若采摘后10天,这种水果失去的新鲜度为10%,采摘后20天,这种水果失去的新鲜度为20%.那么采摘下来的这种水果多长时间后失去40%新鲜度( )
. 若采摘后10天,这种水果失去的新鲜度为10%,采摘后20天,这种水果失去的新鲜度为20%.那么采摘下来的这种水果多长时间后失去40%新鲜度( )
 . 若采摘后10天,这种水果失去的新鲜度为10%,采摘后20天,这种水果失去的新鲜度为20%.那么采摘下来的这种水果多长时间后失去40%新鲜度( )
. 若采摘后10天,这种水果失去的新鲜度为10%,采摘后20天,这种水果失去的新鲜度为20%.那么采摘下来的这种水果多长时间后失去40%新鲜度( )
A . 25天
B . 30天
C . 35天
D . 40天
已知二次函数  满足
满足  ,且
,且  的最小值是
的最小值是  .
.
 满足
满足  ,且
,且  的最小值是
的最小值是  .
.
-
(1) 求
 的解析式;
的解析式;
-
(2) 若关于x的方程
 在区间
在区间 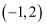 上有唯一实数根,求实数m的取值范围;
上有唯一实数根,求实数m的取值范围;
-
(3) 函数
 ,对任意
,对任意  ,
,  都有
都有  恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
已知离心率为  的椭圆
的椭圆  :
:  (
(  )和离心率为
)和离心率为 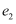 的双曲线
的双曲线  :
:  (
(  ,
,  )有公共的焦点
)有公共的焦点  ,
,  ,P是它们在第一象限的交点,且
,P是它们在第一象限的交点,且  ,则
,则  的最小值为( )
的最小值为( )
 的椭圆
的椭圆  :
:  (
(  )和离心率为
)和离心率为 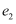 的双曲线
的双曲线  :
:  (
(  ,
,  )有公共的焦点
)有公共的焦点  ,
,  ,P是它们在第一象限的交点,且
,P是它们在第一象限的交点,且  ,则
,则  的最小值为( )
的最小值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
双曲线  和椭圆
和椭圆  有相同的焦点F1 , F2 , M为两曲线的交点,则|MF1|•|MF2|等于( )
有相同的焦点F1 , F2 , M为两曲线的交点,则|MF1|•|MF2|等于( )
 和椭圆
和椭圆  有相同的焦点F1 , F2 , M为两曲线的交点,则|MF1|•|MF2|等于( )
有相同的焦点F1 , F2 , M为两曲线的交点,则|MF1|•|MF2|等于( )
A . a+m
B . b+m
C . a﹣m
D . b﹣m
已知全集  ,集合
,集合 
 ,则
,则  ( )
( )
 ,集合
,集合 
 ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知椭圆  的离心率为
的离心率为  ,右焦点为F , 过F作x轴的垂线交双曲线
,右焦点为F , 过F作x轴的垂线交双曲线  的两条渐近线于E , C , 得到三角形
的两条渐近线于E , C , 得到三角形  的面积为1.
的面积为1.
 的离心率为
的离心率为  ,右焦点为F , 过F作x轴的垂线交双曲线
,右焦点为F , 过F作x轴的垂线交双曲线  的两条渐近线于E , C , 得到三角形
的两条渐近线于E , C , 得到三角形  的面积为1.
的面积为1.
-
(1) 求椭圆C的标准方程;
-
(2) 设P , M , N的三个点都在椭圆C上,设
 的中点为Q , 且
的中点为Q , 且  ,试判断
,试判断  的面积是否为定值,并说明理由.
的面积是否为定值,并说明理由.
已知集合 


A . 



已知向量![]() ,
,![]() ,满足
,满足![]() •
•![]() =0,|
=0,|![]() |=2,|
|=2,|![]() |=1,则|
|=1,则|![]() +2
+2![]() |= .
|= .
已知向量![]() 的夹角为
的夹角为![]() ,
,![]() 的值为
的值为
已知二次函数![]() ,其中
,其中![]()
![]()
(1)若方程![]() 有两个实根
有两个实根![]() ,且方程
,且方程![]() 有两个相等的根,
有两个相等的根,
求![]() 的解析式;
的解析式;
(2)若![]() 的图象与x轴交于A(-3,0),B(m,0)两点, 且当
的图象与x轴交于A(-3,0),B(m,0)两点, 且当![]() 时,
时, ![]() 恒成立.求实数
恒成立.求实数![]() 的取值范围.
的取值范围.
最近更新
- 下图示意阿尔卑斯山和天山某山峰(局部)南北坡自然带垂直变化情况。读图,完成1-3题。1.图中①、②所代表的自然带分别是(
- 氟是一种卤族元素,但它与其他卤素在单质和化合物的制备与性质上存在较明显的差异。 (1)研究发现,SbF5能将MnF4从离
- 所含分子数相同的一组物质是()A. 1gH2和1gN2 B. 1molH2O和1gH2O C. 3.2gO2和4.8gO
- 某植物培养液含有甲、乙、丙三种离子,它们对植物的生长都有影响。下表列出的5种培养液中,甲、乙、丙三种离子的浓度(单位:1
- 已知,则的最大值是( ) A. B.6 C.2
- 甲乙两车在一平直道路上同向运动,其图像如图所示,图中和的面积分别为和.初始时,甲车在乙车前方处。下列说法正确的是 (
- 对于反应C(s)+H2O(g) CO(g)+H2(g) ;ΔH >0,下列有关说法正确的是 ()
- 19. 重为10牛的物体漂浮在液面,用力的图示法在图7中画出物体受到的浮力F。
- Section C (25) Directions :Write an English composition a
- 质量相同的两球,已知甲球的比热容是乙球比热容的2倍,乙球吸收的热量是甲球吸收热量的2倍,那么甲球升高的温度与乙球升高的温
- 如图a、b所示,是一辆质量m=6×103kg的公共汽车在t=0和t=4s末两个时刻的两张照片。当t=0时,汽车刚启动(汽
- 有关有机物说法正确的是 A.用新制氢氧化铜检验淀粉是否完全水解 B.乙醇、乙烷和乙酸都可以与钠反应生
- 抛物线y=(x+2)2+3的顶点坐标是( ) A. (-2,3)
- 中国移动公司有神州行和大众卡两种业务。神州行免月租,打市内电话0.39元/分;大众卡月租16元,打市内通话0.15元/分
- 下列有关化学反应速率的说法不正确的是 () A.化学反应达
- 读图,分析回答:图中②地区绿洲退化严重,对这一现象形成的原因,下列推测成立的是: ①人口增长迅速 ②气候变暖,蒸发量增大
- 国外有人将野外小溪、瀑布、小河流水、鸟鸣等声音录下来,复制出录音带高价在城里出售,卖“声音”卖出了财路。录制的声音之所以
- 阅读下面语段,按要求回答问题: 白日梦:指一种适度的意识状态的改变形式,注意力不再诉诸对环境刺激的反应,而是转向对内在刺
- 对我国影响最大的气候灾害是() A.旱涝 B.台风 C.梅雨 D.寒潮
- (8分)在平直公路上以12m/s的速度行驶的汽车,因故以4m/s2的加速度紧急刹车,求: (1)2s末汽车速度;



