高中 数学
 ,半径OA为1km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成.其中D在线段OB上,且CD∥AO,设∠AOC=θ,
,半径OA为1km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成.其中D在线段OB上,且CD∥AO,设∠AOC=θ,
-
(1) 用θ表示CD的长度,并写出θ的取值范围.
-
(2) 当θ为何值时,观光道路最长?
 ),则y=f(x)的解析式为.
),则y=f(x)的解析式为.
 为增函数,则实数
为增函数,则实数  的取值范围为( )
的取值范围为( )
 B . [1,+∞)
C .
B . [1,+∞)
C .  D .
D . 
 ,则
,则  的值等于( )
的值等于( )
 B .
B .  C .
C .  D .
D . 
 ,前n项和为Sn , 且
,前n项和为Sn , 且 
-
(1) 求数列{an}的通项
-
(2) 如果bn=3(n+1)×2n•an , 求数列{bn}的前n项和Tn .
 ,若对任意实数
,若对任意实数  都有
都有  ,则实数
,则实数  的取值范围是
的取值范围是 .
 ,
,  满足
满足  ,
,  ,
,  ,则
,则  的前10项之和为( )
的前10项之和为( )
 B .
B . 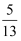 C .
C .  D .
D . 

在两次运行这个程序时,第一次输入8和4,第二次输入2和4,则两次运行后输出的结果分别为 ( )
 满足
满足  ,且
,且  ,则向量
,则向量  与
与  的夹角为.
的夹角为.
 ,
,  , 且
, 且 , 则
, 则 的值为( )
的值为( )
已知向量![]() =(2,-1),
=(2,-1),![]() =(-1,m),且
=(-1,m),且![]() ________
________
当![]() 时,执
时,执![]() 行如图所示的程序框图,输出的
行如图所示的程序框图,输出的![]() 值为( )
值为( )
A.6 B.8 C.14 D.30

定义域为![]() 的函数
的函数![]() ,其导函数为
,其导函数为![]() .若对
.若对![]() ,均有
,均有![]() ,则称函数
,则称函数![]() 为
为![]() 上的梦想函数.
上的梦想函数.
(Ⅰ)已知函数![]() ,试判断
,试判断![]() 是否为其定义域上的梦想函数,并说明理由;
是否为其定义域上的梦想函数,并说明理由;
(Ⅱ)已知函数![]() (
(![]() ,
,![]() )为其定义域上的梦想函数,求
)为其定义域上的梦想函数,求![]() 的取值范围;
的取值范围;
(Ⅲ)已知函数![]() (
(![]() ,
,![]() )为其定义域上的梦想函数,求
)为其定义域上的梦想函数,求![]() 的最大整数值.
的最大整数值.
各项均为正数的等比数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() ,
,![]() ,则
,则![]() ______.
______.
设全集![]() ,
,![]() ,
,![]() ,则图中阴影部分表示的集合为(
,则图中阴影部分表示的集合为( ![]() )
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()

已知二次函数![]() 的两个零点分别在区间
的两个零点分别在区间![]() 和
和![]() 内,则
内,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
一个单位有职工160人,其中业务人员96人,管理人员40人,后勤服务人员24人。为了了解职工的某种情况,要从中抽取一个容量为20的样本,按下述三种方法抽取:①将160人从1-160编号,然后用白纸做成1-160号的签160个放入箱内拌匀,然后从中抽取20个签,与签号相同的20个人被选出;②将160人从1-160编号,按编号顺序分成20组,每组8人,即1-8号,9-16号,…,153-160号。先从第1组中用抽签方法抽出![]() 号
号![]() ,其余组的按(
,其余组的按(![]() )号
)号![]() 亦被抽出,如此抽取20人③按20:160=1:8的比例,从业务人员中抽取12人,从管理人员中抽取5人,从后勤人员中抽取3人,都用随机数表法从各类人员中抽取所需的人数,他们合在一起恰好抽到20人。
亦被抽出,如此抽取20人③按20:160=1:8的比例,从业务人员中抽取12人,从管理人员中抽取5人,从后勤人员中抽取3人,都用随机数表法从各类人员中抽取所需的人数,他们合在一起恰好抽到20人。
上述三种抽样方法,按简单随机抽样、分层抽样、系统抽样的顺序是( )
A.①、②、③ B.②、①、③ C.①、③、② D.③、①、②、
- Take great pains to read _____ you can or you won't have a b
- 已知函数f(x)=lnx+tanα(α∈(0,))的导函数为,若使得=成立的<1,则实数α的取值范围为( ) A.
- Maryworked here as a______secretary and I ended up getting
- 电动自行车提供能量的装置为装在电池盒内的电池组,当它给电动机供电时,电动机将带动车轮转动。假设有一辆电动自行车,人和车的
- Hehad once been withdrug dealings, but evidence f
- —Many people have been out of work in China. —And ________
- “士别三日,当刮目相看。”这句话要求我们: A.世界上没有僵死的、一成不变的事物 B.世界上一切事物都是变化发展的C.
- 阅读《欣赏使人美丽》一文,完成下面题目。(10分)①面对同一棵树,有人看到绿叶,有人看到了毛毛虫。真诚的人能够感知到他人
- 右图是甲、乙两种固体的溶解度曲线。下列说法中错误的是 A.t1℃时,50 g水中最多溶解15 g甲 B.t2℃时,甲、乙
- At last they climbed up the mountain,on the top of which
- My aunt always losesher way when she is out by herself,becau
- 经济、政治和文化是社会生活的三个基本领域。回答下面试题。 参加村委会或居委会选举,参观自然博物馆和历史博物馆的各种展览,
- We must find a dictionary. ____ will do. A. Some B. Any C. E
- BaCl2有剧毒,致死量为0.8g,万一不慎误服,应大量吞服鸡蛋清来解毒,并加服一定量药剂,此药剂的主要成分是(
- 计算:+|2−3|+sin245°
- 物体静止在光滑水平面上.先施加一水平向右的恒力F1,经t时间后撤去F1,,立刻施加另一水平向左的恒力F2,又经t时间后物
- It was very cold ____ they still went swimming. A. although
- 在古代,中国的科学技术成就长期处于世界前列,对整个人类文明的发展作出了巨大贡献。总的说来,我国古代科学技术注重实际运用,
- 下列各组词语中,没有错别字的一组是 A.桎梏 气慨 概念化 民生凋敝 B.警惕 亵读 珊瑚
- 在中古的西欧,一个男人的梦想和最高荣誉是 A.成为贵族 B.成为绅士 C.成为武士



