高中 数学
如图,在四棱锥  中,
中,  平面
平面  ,
, 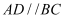 ,
,  ,
,  ,
,  ,
,  .
.
 中,
中,  平面
平面  ,
, 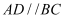 ,
,  ,
,  ,
,  ,
,  .
. 
(Ⅰ)求异面直线  与
与  所成角的正弦值;
所成角的正弦值;
(Ⅱ)若三棱锥  体积为2,求
体积为2,求  的长.
的长.
已知函数  是奇函数.
是奇函数.
 是奇函数.
是奇函数.
-
(1) 求a的值;
-
(2) 求解不等式
 ;
;
-
(3) 当
 时,
时,  恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
已知△ABC利用斜二测画法画出的直观图是边长为2的正三角形,则△ABC的面积为( )
A .  B . 2
B . 2 C .
C . 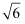 D . 2
D . 2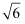
 B . 2
B . 2 C .
C . 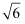 D . 2
D . 2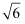
若抛物线C:y2=4x上一点A到抛物线焦点的距离为4,则点A到坐标原点O的距离为.
在  中,
中,  所对的边长分别为
所对的边长分别为  ,若
,若  ,则
,则  =.
=.
 中,
中,  所对的边长分别为
所对的边长分别为  ,若
,若  ,则
,则  =.
=.
若双曲线  ﹣
﹣  =1(a>0,b>0)的一条渐近线方程为y=
=1(a>0,b>0)的一条渐近线方程为y=  x,则该双曲线的离心率为( )
x,则该双曲线的离心率为( )
 ﹣
﹣  =1(a>0,b>0)的一条渐近线方程为y=
=1(a>0,b>0)的一条渐近线方程为y=  x,则该双曲线的离心率为( )
x,则该双曲线的离心率为( )
A .  B . 3
C .
B . 3
C .  D . 2
D . 2
 B . 3
C .
B . 3
C .  D . 2
D . 2
设复数  在复平面内的对应点关于实轴对称,
在复平面内的对应点关于实轴对称,  则
则  ( )
( )
 在复平面内的对应点关于实轴对称,
在复平面内的对应点关于实轴对称,  则
则  ( )
( )
A . 25
B . -25
C .  D .
D . 
 D .
D . 
已知函数  (
(  且
且  )的零点是
)的零点是  .
.
 (
(  且
且  )的零点是
)的零点是  .
.
-
(1) 设曲线
 在零点处的切线斜率分别为
在零点处的切线斜率分别为  ,判断
,判断  的单调性;
的单调性;
-
(2) 设
 是
是  的极值点,求证:
的极值点,求证:  .
.
已知函数  ,则
,则  ( )
( )
 ,则
,则  ( )
( )
A . -1
B . 2
C . 1
D . 5
已知函数  ,且
,且  ,
,  ,
,  ,
,  ,则( )
,则( )
 ,且
,且  ,
,  ,
,  ,
,  ,则( )
,则( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知α为锐角,且  ,函数
,函数  ,数列{an}的首项a1=1,an+1=f(an).
,数列{an}的首项a1=1,an+1=f(an).
 ,函数
,函数  ,数列{an}的首项a1=1,an+1=f(an).
,数列{an}的首项a1=1,an+1=f(an).
-
(1) 求函数f(x)的表达式;
-
(2) 求证:数列{an+1}为等比数列;
-
(3) 求数列{an}的前n项和Sn .
已知向量  ,
,  ,当
,当 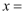 时,
时,  .
.
 ,
,  ,当
,当 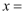 时,
时,  .
.
2017年“一带一路”国际合作高峰论坛于今年5月14日至15日在北京举行.为高标准完成高峰论坛会议期间的志愿服务工作,将从27所北京高校招募大学生志愿者,某调查机构从是否有意愿做志愿者在某高校访问了80人,经过统计,得到如下丢失数据的列联表:(  ,表示丢失的数据)
,表示丢失的数据)
 ,表示丢失的数据)
,表示丢失的数据)无意愿 | 有意愿 | 总计 | |
男 |
|
| 40 |
女 | 5 |
|
|
总计 | 25 |
| 80 |
附参考公式及数据:  ,其中
,其中  .
.
| 0.40 | 0.25 | 0.10 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.706 | 6.635 | 7.879 | 10.828 |
-
(1) 求出
 的值,并判断:能否有99.9%的把握认为有意愿做志愿者与性别有关;
的值,并判断:能否有99.9%的把握认为有意愿做志愿者与性别有关;
-
(2) 若表中无意愿做志愿者的5个女同学中,3个是大学三年级同学,2个是大学四年级同学.现从这5个同学中随机选2同学进行进一步调查,求这2个同学是同年级的概率.
在四棱锥  中,
中,  ,
,  .
.  为
为  的中点.
的中点.
 中,
中,  ,
,  .
.  为
为  的中点.
的中点. 
-
(1) 若点
 为
为  的中点,求证:
的中点,求证:  平面
平面  ;
;
-
(2) 当平面
 平面
平面  时,线段
时,线段  上是否存在一点
上是否存在一点  ,使得平面
,使得平面  与平面
与平面  所成锐二面角的大小为
所成锐二面角的大小为  ?若存在,求出点
?若存在,求出点  的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
定义在R上的函数  ,给出下列三个论断:
,给出下列三个论断:
 ,给出下列三个论断:
,给出下列三个论断: ①  在R上单调递增;②
在R上单调递增;② 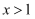 ;③
;③  .
.
以其中的两个论断为条件,余下的一个论断为结论,写出一个正确的命题:.
在![]() 中,角A,B,C所对的边分别为
中,角A,B,C所对的边分别为![]() ,且满足
,且满足![]() .
.
(Ⅰ)求角![]() 的大小;
的大小;
(Ⅱ)求![]() 的最大值,并求取得最大值时角A、B的大小。
的最大值,并求取得最大值时角A、B的大小。
已知等比数列![]() 的公比为
的公比为![]() ,记
,记![]() ,
,![]()
![]()
![]()
![]() ,则以下结论一定正确的是( )
,则以下结论一定正确的是( )
A. 数列![]() 为等差数列,公差为
为等差数列,公差为![]() B. 数列
B. 数列![]() 为等比数列,公比为
为等比数列,公比为![]()
C. 数列![]() 为等比数列,公比为
为等比数列,公比为![]() D. 数列
D. 数列![]() 为等比数列,公比为
为等比数列,公比为![]()
已知函数 ![]() 的定义域为
的定义域为 ![]() ,若对于任意的
,若对于任意的 ![]() ,
,![]() ,都有
,都有 ![]() ,且当
,且当 ![]() 时,有
时,有 ![]() .
.
(1)证明:![]() 为奇函数;
为奇函数;
![]() (2)判断
(2)判断 ![]() 在
在 ![]() 上的
上的![]() 单调性,并证明;
单调性,并证明;
(3)设 ![]() ,若
,若 ![]() (
(![]() 且
且 ![]() )对
)对 ![]() 恒成立,求实数
恒成立,求实数 ![]() 的取值范围.
的取值范围.
过坐标轴上一点 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为 、
、 .若
.若 ,则
,则 的取值范围是( )
的取值范围是( )
A. B.
B. 
C. D.
D. 
A.
C.
最近更新
- 若将浓盐酸和浓硫酸敞口放置在空气中,一段时间后,可以肯定的是( )A.溶质质量都减少B.溶剂质量都增大C.溶液质量都增大
- .如图所示的电路中,甲、乙两灯泡串联,观察到甲灯泡比乙灯泡亮.则下列描述中错误的是 A.P甲>P乙
- 观察下列各式及其展开式:…… 请你猜想 的展开式第三项的系数是( )A . 13B . 15C . 20D . 25
- 读图,完成7~8题。7.下列关于图示区域资源状况的叙述,正确的是() A.河网密布,水资源丰富 B.临近海洋,地热资源丰
- 依次填入下列各句空格上的熟语,与句意最贴切的一项是( ) ①在作者笔下,钗黛这两个姑娘,常常 加以评说的。 ②
- —Would you mind my smoking here? —_______It’s not allowed he
- 绝大多数的动物都需要从环境中获得氧气用于完成各项生理活动,你知道蚯蚓是通过什么结构与周围环境进行气体交换吗( )
- It is the protection for the trees___________ really matter
- 问:机械效率总小于1吗?
- Rather than _______everything to the last minute, I always
- 草酸(H2C2O4)是一种有机酸,其水溶液呈酸性。它广泛分布于植物、动物和真菌题中,并在不同的生命体中发挥不同的功能。下
- 一个民族必须要有自己的特色文化,否则必将成为外来文化的虏役与附庸,最终在这个世界上消失。要保持自己民族的特色,那就要求一
- (云南省牟定一中2010届高三上学期9月月考)下列各句中,没有语病的一句是 ( )
- 我国城市建设中“南方北方一个样,大城小城一个样,城里城外一个样”,这种“千城一面”现象 A.体现了当代世界建筑文化的发展
- 下列物质与危险化学品标志的对应关系不正确的是A B C D 汽油 天然气 浓硫酸 氢氧化钠
- 九十多年来的实践证明,中国在继承辛亥革命的爱国主义精神的同时又超越了辛亥革命的历史局限,谱写了中华民族自强不息、顽强奋进
- 下列两种气体的分子数一定相等的是( ) A.质量相等,密度不等的N2和C2H4
- 设二次函数的值域为,则的最大值为
- x(x﹣6)=x.
- In Singapore,a southern Asian country, the Chinese thel








