高中 数学
如图,点  是正方体
是正方体  中的侧面
中的侧面  上的一个动点,则下列结论正确的是( )
上的一个动点,则下列结论正确的是( )
 是正方体
是正方体  中的侧面
中的侧面  上的一个动点,则下列结论正确的是( )
上的一个动点,则下列结论正确的是( ) 
A . 点  存在无数个位置满足
存在无数个位置满足  B . 若正方体的棱长为1,三棱锥
B . 若正方体的棱长为1,三棱锥  的体积最大值为
的体积最大值为  C . 在线段
C . 在线段  上存在点
上存在点  ,使异面直线
,使异面直线  与
与  所成的角是30°
D . 点
所成的角是30°
D . 点  存在无数个位置满足
存在无数个位置满足  平面
平面 
 存在无数个位置满足
存在无数个位置满足  B . 若正方体的棱长为1,三棱锥
B . 若正方体的棱长为1,三棱锥  的体积最大值为
的体积最大值为  C . 在线段
C . 在线段  上存在点
上存在点  ,使异面直线
,使异面直线  与
与  所成的角是30°
D . 点
所成的角是30°
D . 点  存在无数个位置满足
存在无数个位置满足  平面
平面 
某学员在一次射击测试中射靶6次,命中环数如下:9,5,8,4,6,10,
则:
平均命中环数为;命中环数的方差为.
在  中,
中,  为
为  边上的中线,点
边上的中线,点  满足
满足  ,则
,则  ( )
( )
 中,
中,  为
为  边上的中线,点
边上的中线,点  满足
满足  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
函数  ,则
,则  .
.
 ,则
,则  .
.
已知直线 与圆
与圆 相切,则实数a的值为.
相切,则实数a的值为.
 与圆
与圆 相切,则实数a的值为.
相切,则实数a的值为.
函数  的零点所在的区间为( )
的零点所在的区间为( )
 的零点所在的区间为( )
的零点所在的区间为( )
A . 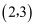 B .
B .  C .
C . 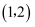 D .
D . 
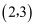 B .
B .  C .
C . 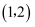 D .
D . 
已知A(4,0,2),B(2,﹣6,2),点M在x轴上,且到A,B两距离相等,则M的坐标为( )
A . (﹣6,0,0)
B . (0,﹣6,0)
C . (0,0,﹣6)
D . (6,0,0)
已知随机变量ξ服从正态分布N(1,σ2),P(ξ≤4)=0.79,则P(﹣2≤ξ≤1)=( )
A . 0.21
B . 0.58
C . 0.42
D . 0.29
已知四棱锥 , 底面ABCD是平行四边形,且
, 底面ABCD是平行四边形,且 . 侧面PCD是边长为2的等边三角形,且平面
. 侧面PCD是边长为2的等边三角形,且平面 平面ABCD.点E在线段PC上,且直线
平面ABCD.点E在线段PC上,且直线 平面BDE.
平面BDE.
 , 底面ABCD是平行四边形,且
, 底面ABCD是平行四边形,且 . 侧面PCD是边长为2的等边三角形,且平面
. 侧面PCD是边长为2的等边三角形,且平面 平面ABCD.点E在线段PC上,且直线
平面ABCD.点E在线段PC上,且直线 平面BDE.
平面BDE.
-
(1) 求证:
 ;
;
-
(2) 设二面角
 的大小为
的大小为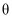 , 且
, 且 . 求直线BE与平面ABCD所成的角的正切值.
. 求直线BE与平面ABCD所成的角的正切值.
已知幂函数  的图象关于y轴对称,且在
的图象关于y轴对称,且在 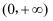 上是减函数,若
上是减函数,若  ,则实数a的取值范围是( )
,则实数a的取值范围是( )
 的图象关于y轴对称,且在
的图象关于y轴对称,且在 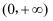 上是减函数,若
上是减函数,若  ,则实数a的取值范围是( )
,则实数a的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知向量  ,其中
,其中  与
与  是相反向量,且
是相反向量,且  ,
,  ,则
,则  ( )
( )
 ,其中
,其中  与
与  是相反向量,且
是相反向量,且  ,
,  ,则
,则  ( )
( )
A .  B .
B .  C . 2
D .
C . 2
D . 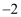
 B .
B .  C . 2
D .
C . 2
D . 
已知实数 , 平面向量
, 平面向量 . 满足
. 满足 . 若存在唯一实数
. 若存在唯一实数 , 使得
, 使得 , 则
, 则 的最小值是
的最小值是
 , 平面向量
, 平面向量 . 满足
. 满足 . 若存在唯一实数
. 若存在唯一实数 , 使得
, 使得 , 则
, 则 的最小值是
的最小值是
实数  ,
,  满足
满足  ,则
,则  的最大值为.
的最大值为.
 ,
,  满足
满足  ,则
,则  的最大值为.
的最大值为.
已知函数  ,则“
,则“  ”是“
”是“  ”的( )
”的( )
 ,则“
,则“  ”是“
”是“  ”的( )
”的( )
A . 充分不必要条件
B . 必要不充分条件
C . 充要条件
D . 既不充分也不必要条件
已知θ∈(0,π)且sinθ,cosθ是方程25x2﹣5x﹣12=0的两个实根,求tanθ﹣  的值.
的值.
 的值.
的值.
在![]() 的二项展开式中,
的二项展开式中,![]() 的系数为
的系数为
![]()
已知以角![]() 为钝角的
为钝角的![]() 的内角A、B、C的对边分别为a、b、c,
的内角A、B、C的对边分别为a、b、c,![]() ,且
,且![]() (1)求角
(1)求角![]() 的大小;(2)求
的大小;(2)求![]() 的取值范围.
的取值范围.
已知函数![]() 是
是![]() 上的偶函数,且在
上的偶函数,且在![]() 上单调递增,则下列各式成立的是( )
上单调递增,则下列各式成立的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
设![]() 为可导函数,且满足
为可导函数,且满足![]() ,则函数
,则函数![]() 在
在![]() 处的导数值为( )
处的导数值为( )
A. 1 B. ![]() C. 1或
C. 1或![]() D. 以上答案都不对
D. 以上答案都不对
已知函数y=f(x)=-x3+ax2+b(a,b∈R).
(1)当a>0时,若f(x)满足:y极小值=1,y极大值=![]() ,试求f(x)的解析式;
,试求f(x)的解析式;
(2)若x∈[0,1]时,y=f(x)图象上的任意一点处的切线斜率k满足:|k|≤1,求a的取值范围.
最近更新
- +R′CH2COOC2H5 聚乙烯醇肉桂酸酯是最早用于光刻胶的光敏高分子化合物,其合成途径如下: 合成步骤一:合成步骤
- 堆放时间较长的大白菜会因发热而腐烂,能使大白菜产生热量的生理活动是A.光合作用 B.呼吸作用
- 据《夷氛闻记》记载:“(夷兵舍命突围出)无奈人如山积,围开复合,各弃鸟枪徒手延颈待戮,乞命之声震山谷”。这说明三元里人民
- 关于21三体综合征的叙述,错误的是 ( )
- 下列关于性状和基因的关系,描述正确的一项是( ) A.基因控制着性状 B.性状控制着基因 C.有些性状不受基因控制D.基
- 点P(x,y)在直线x+y-4=0上,O是原点,则|OP|的最小值是( )A. B.2
- 材料一:在商店售货员推荐下,小杰买了一部价格不菲的MP3,使用不到一天就发现有严重的质量问题。小杰去退换时,商家却坚持“
- 如图15所示,两块平行金属板竖直放置,两板间的电势差U=1.5×103 V(仅在两板间有电场),现将一质量m=1×10-
- 《三国演义》第四十二回“张翼德大闹长坂桥”中,张飞三声大喝吓死曹操一方的夏侯杰,并使曹军仓皇逃窜,刘备却为何说他“勇则勇
- 在从花到果实的发育过程中,花的各部分结构发生什么变化?用连线的方式表示出来。 ①花瓣 ②雄蕊 A.胚 ③花柱
- 下列四幅图中,表示当今海陆分布的是( )
- The Parkers bought a new house, but____will need a lot of wo
- 我国发射的探月卫星有一类为绕月极地卫星。利用该卫星可对月球进行成像探测。如图8所示,设卫星在绕月极地轨道上做圆周运动时距
- 根据化学反应的实质是旧键断裂、新键形成的观点,下列变化没有发生化学键断裂的是( ) A.溴蒸气被活性炭吸附 B.电
- 一个几何体的三视图如下所示,则该几何体的表面积是( )A. B. C. D.
- 影响人口迁移的诸多因素中,经济因素往往起着重要作用。
- 现有氨基酸700个,其中氨基总数为710个,羧基总数为708个,则由这些氨基酸合成的含有2条肽链的蛋白质共有肽键、氨基和
- 已知x=2是一元二次方程x2+mx﹣2=0的一个解,则m的值是() A.1 B.﹣1 C.﹣3 D.0或﹣1
- 一定温度下,在1 L的密闭容器中,X、Y、Z三种气体的物质的量随时间变化的曲线如右图所示。下列描述正确的是 A.反应开始
- 下列对美国近代侵华活动的表述,不正确的是( )A.《望厦条约》严重破坏了中国的领海主权 B.1900年美国军队侵入



