高中 数学
三国时期我国的数学家赵爽曾创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形,其中直角三角形中较小的锐角  满足
满足  ,现在向该正方形区域内随机投掷一枚飞镖,则飞镖落在小正方形内的概率是( )
,现在向该正方形区域内随机投掷一枚飞镖,则飞镖落在小正方形内的概率是( )
 满足
满足  ,现在向该正方形区域内随机投掷一枚飞镖,则飞镖落在小正方形内的概率是( )
,现在向该正方形区域内随机投掷一枚飞镖,则飞镖落在小正方形内的概率是( )
A . 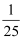 B .
B .  C .
C . 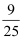 D .
D . 
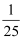 B .
B .  C .
C . 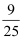 D .
D . 
校庆杯篮球赛期间,安排了投篮比赛游戏,现有20名同学参加投篮比赛,已知每名同学投进的概率均为0.6,每名同学有2次投篮机会,且各同学投篮之间没有影响,现规定:投进两个得4分,投进一个得2分,一个未进得0分,则一名同学投篮得2分的概率为.
已知函数  .(无理数
.(无理数  )
)
 .(无理数
.(无理数  )
)
-
(1) 若
 在
在  单调递增,求实数
单调递增,求实数  的取值范围;
的取值范围;
-
(2) 当
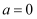 时,设函数
时,设函数  ,证明:当
,证明:当  时,
时,  .(参考数据
.(参考数据  )
)
若  的定义域为
的定义域为  ,且
,且  是奇函数,当
是奇函数,当  时,
时,  ,则当
,则当 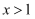 时,函数
时,函数  的递减区间是.
的递减区间是.
 的定义域为
的定义域为  ,且
,且  是奇函数,当
是奇函数,当  时,
时,  ,则当
,则当 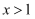 时,函数
时,函数  的递减区间是.
的递减区间是.
阅读如图所示的程序框图,运行相应的程序,则输出的结果为( )

A . 2
B . 1
C . 0
D . ﹣1
如图,在△ABC中,N为线段AC上接近A点的四等分点,若  ,则实数m的值为( )
,则实数m的值为( )
 ,则实数m的值为( )
,则实数m的值为( ) 
A .  B .
B .  C . 1
D . 3
C . 1
D . 3
 B .
B .  C . 1
D . 3
C . 1
D . 3
已知函数f(x)=x﹣alnx(a∈R)
-
(1) 当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
-
(2) 求函数f(x)的极值.
如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1.
(I)设点E在线段PC上,若  ,求证:DE∥平面PAB;
,求证:DE∥平面PAB;
(II)求证:平面PBC⊥平面PAB.

已知 为非直角三角形,
为非直角三角形, .
.
 为非直角三角形,
为非直角三角形, .
.
-
(1) 证明:
 ;
;
-
(2) 求
 的最小值.
的最小值.
已知x>0,y>0,且 +
+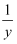 =1,若x+2y>m2+2m恒成立,则实数m的取值范围是( )
=1,若x+2y>m2+2m恒成立,则实数m的取值范围是( )
 +
+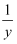 =1,若x+2y>m2+2m恒成立,则实数m的取值范围是( )
=1,若x+2y>m2+2m恒成立,则实数m的取值范围是( )
A . (0,2]
B . (0,2)
C . (﹣4,2)
D . (﹣2,4)
已知3sin(π﹣α)+cos(2π﹣α)=0.
-
(1) 求

-
(2) 求

-
(3) 求
 .
.
已知圆  的标准方程为
的标准方程为  ,则它的圆心坐标是( )
,则它的圆心坐标是( )
 的标准方程为
的标准方程为  ,则它的圆心坐标是( )
,则它的圆心坐标是( )
A . 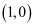 B .
B .  C .
C . 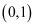 D .
D . 
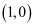 B .
B .  C .
C . 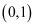 D .
D . 
若双曲线  :
:  与双曲线
与双曲线  :
:  的渐近线相同,则双曲线
的渐近线相同,则双曲线  的离心率为( )
的离心率为( )
 :
:  与双曲线
与双曲线  :
:  的渐近线相同,则双曲线
的渐近线相同,则双曲线  的离心率为( )
的离心率为( )
A .  B .
B .  C .
C . 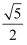 D .
D . 
 B .
B .  C .
C . 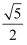 D .
D . 
已知函数 .
.
 .
.
-
(1) 求函数
 的单调递增区间;
的单调递增区间;
-
(2) 已知
 , 若函数
, 若函数 在区间[0,
在区间[0, ]上恰好有两个零点,求a的取值范围.
]上恰好有两个零点,求a的取值范围.
已知集合 ,集合
,集合 ,则
,则 等于 ( )
等于 ( )
 ,集合
,集合 ,则
,则 等于 ( )
等于 ( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知正方体![]() ,
,

(1)证明:![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成的角.
所成的角.
曲线![]() 在点
在点![]() 处的切线方程为___________.
处的切线方程为___________.
由某种设备的使用年限xi(年)与所支出的维修费yi(万元)的数据资料算得如下结果.![]()
(1)求所支出的维修费y对使用年限x的线性回归方程![]()
(2)①判断变量x与y之间是正相关还是负相关;
②当使用年限为8年时,试估计支出的维修费是多少.
三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明,下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实,图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实,黄实,利用2×勾×股+(股﹣勾)2=4×朱实+黄实=弦实,化简,得勾2+股2=弦2 , 设勾股中勾股比为1: ![]() ,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )

A.866 B.500 C.300 D.134
在直角坐标系 中,以坐标原点为极点,
中,以坐标原点为极点, 轴正半轴为极坐标建立极坐标系,圆
轴正半轴为极坐标建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .
.
 求
求 的普通方程;
的普通方程;
 将圆
将圆 平移,使其圆心为
平移,使其圆心为 ,设
,设 是圆
是圆 上的动点,点
上的动点,点 与
与 关于原点
关于原点 对称,线段
对称,线段 的垂直平分线与
的垂直平分线与 相交于点
相交于点 ,求
,求 的轨迹的参数方程.
的轨迹的参数方程.
最近更新
- 下列有关膜的叙述,错误的是 ( ) A.细胞膜主要有脂质和蛋白质组成 B.细胞膜中还有少
- 提出人类和类人猿的共同祖先是森林古猿这一观点的学者是( ) A.巴斯德 B.孟德尔 C.达
- 一个小儿醒目的站立在象征宗祠的屋顶下,这便是汉字的“字”。“字”的造字意图可以理解为,把新生命领到天地、祖先面前,通过某
- 某同学为了测量某一节干电池的电动势和内阻,实验室准备了下列器材:A.待测干电池E(电动势约为1.5 V,内阻约为1 Ω)
- 短周期主族元素X、Y、Z、W的原子序数依次增大。X原子的最外层电子数是其内层电子数的2倍,Y是地壳中含量最高的元素,Z2
- 黄梅戏表演艺术家韩再芬尝试在民间艺术中融入“时尚”元素。她主演的《徽州女人》,使用了大量充满现代感的电影、舞蹈语言,同时
- 2.3 g钠在干燥的空气中与氧气反应,可得3.5 g固体(假设产物不发生化学反应),据此可判断其产物为() A.只有Na
- 一定温度下,在恒容密闭容器中进行:2SO2(g)+O2(g)2SO3(g),若开始时充入2molSO2和2molO2,反
- 下面四个结论:①偶函数的图象一定与y轴相交;②奇函数的图象一定通过原点; ③偶函数的图象关于y轴对称;④既是奇函数又是偶
- 如图所示装置处于静止状态,不计滑轮重和绳重,如果物体的重分别为G1和G2, 那么G1和G2的关系是( )A
- 2010年4月14日青海玉树县发生7.1级强烈地震。“地震无情,人间有爱”。回答下题。 正在出访的总书记提前回国,主持召
- 下列A ~ F是初中化学中的六个实验装置,请按要求填空: (1)A实验试管2中产生的气体是 ▲ ,试管1和2
- 学习完中国近代史以后,小峰同学用年代尺来记录了重大的历史事件,其中对“1840---1949年”的历史阶段特征表述最准确
- Everyoneneeds friends. We all like to feel close to someone.
- .右图为铜锌原电池示意图,下列说法正确的是( ) A.负极发生氧化反应 B.烧杯中的溶液变为蓝色 C.电子由铜片通
- 下图装置可用于( )A.加热NaHCO3制CO2 B.用Cu与稀HNO3
- 已知f(n)=sinπ,则f(1)+f(2)+…+f(2 005)+f(2 006)的值等于( )A.
- “马克思主义……绝不是离开世界文明发展大道而产生的一种故步自封、僵化不变的学说。”材料说明马克思主义的突出特点是()A.
- 气相合成金刚石薄膜被誉为20世纪的炼金术。其中化学气相沉积法制造金刚石薄膜的原理为:CH4 →C(金刚石)+2H2。该反
- 求的单调递增区间。



