高中 数学
已知集合A={y|y=lgx,x>1},B={x|0<|x|≤2,x∈Z}则下列结论正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
由  组成没有重复数字的五位奇数有个.
组成没有重复数字的五位奇数有个.
 组成没有重复数字的五位奇数有个.
组成没有重复数字的五位奇数有个.
如图,在三棱锥  中,
中,  ,
,  ,
,  分别为棱
分别为棱  ,
,  ,
,  的中点.已知
的中点.已知  ,
,  ,
,  ,
, 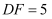 .
.
 中,
中,  ,
,  ,
,  分别为棱
分别为棱  ,
,  ,
,  的中点.已知
的中点.已知  ,
,  ,
,  ,
, 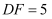 .
.

-
(1) 求证:平面
 平面
平面  ;
;
-
(2) 求二面角
 平面角的余弦值.
平面角的余弦值.
已知命题p:实数m满足m2﹣7am+12a2<0(a>0),命题q:实数m满足方程 表示焦点在y轴上的椭圆,且非q是非p的充分不必要条件,求a的取值范围.
表示焦点在y轴上的椭圆,且非q是非p的充分不必要条件,求a的取值范围.
 表示焦点在y轴上的椭圆,且非q是非p的充分不必要条件,求a的取值范围.
表示焦点在y轴上的椭圆,且非q是非p的充分不必要条件,求a的取值范围.
将函数y=  的定义域为.
的定义域为.
 的定义域为.
的定义域为.
已知函数 , 在
, 在 处切线的斜率为-2.
处切线的斜率为-2.
 , 在
, 在 处切线的斜率为-2.
处切线的斜率为-2.
-
(1) 求
 的值及
的值及 的极小值;
的极小值;
-
(2) 讨论方程
 的实数解的个数.
的实数解的个数.
已知 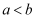 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
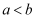 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A . 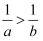 B .
B .  C .
C .  D .
D . 
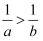 B .
B .  C .
C .  D .
D . 
若直线  与直线
与直线  平行,则
平行,则  .
.
 与直线
与直线  平行,则
平行,则  .
.
某企业生产一种机器的固定成本为0.5万元,但每生产1百台时,又需可变成本(即另增加投入)0.25万元.市场对此商品的年需求量为5百台,销售的收入(单位:万元)函数为:R(x)=5x﹣  x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
 x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
-
(1) 将利润表示为产量的函数;
-
(2) 年产量是多少时,企业所得利润最大?
已知 
 ),当
),当  时
时  ,则实数a的取值范围为 ( )
,则实数a的取值范围为 ( )

 ),当
),当  时
时  ,则实数a的取值范围为 ( )
,则实数a的取值范围为 ( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设 P;“ ”, q:“直线
”, q:“直线 与抛物线
与抛物线 只有一个公共点”,则p是q( )条件
只有一个公共点”,则p是q( )条件
 ”, q:“直线
”, q:“直线 与抛物线
与抛物线 只有一个公共点”,则p是q( )条件
只有一个公共点”,则p是q( )条件
A . 充分且非必要
B . 必要且非充分
C . 充分且必要
D . 既非充分也非必要
若函数 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减,则
上单调递减,则 ( )
( )
 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减,则
上单调递减,则 ( )
( )
A . 3
B . 2
C .  D .
D . 
 D .
D . 
已知圆  与
与  轴负半轴的交点为A,点
轴负半轴的交点为A,点  在直线
在直线  上,过点
上,过点  作圆
作圆  的切线,切点为
的切线,切点为  .
.
 与
与  轴负半轴的交点为A,点
轴负半轴的交点为A,点  在直线
在直线  上,过点
上,过点  作圆
作圆  的切线,切点为
的切线,切点为  .
.
-
(1) 若
 ,切点
,切点  ,求直线
,求直线  ;
;
-
(2) 若
 ,求实数
,求实数  的取值范围.
的取值范围.
设  分别为双曲线
分别为双曲线  的左、右焦点,过
的左、右焦点,过  的直线
的直线  与
与  相切,
相切,  与
与  的渐近线在第一象限内的交点是
的渐近线在第一象限内的交点是  ,若
,若  轴,则双曲线的离心率等于( )
轴,则双曲线的离心率等于( )
 分别为双曲线
分别为双曲线  的左、右焦点,过
的左、右焦点,过  的直线
的直线  与
与  相切,
相切,  与
与  的渐近线在第一象限内的交点是
的渐近线在第一象限内的交点是  ,若
,若  轴,则双曲线的离心率等于( )
轴,则双曲线的离心率等于( )
A .  B . 2
C .
B . 2
C .  D . 4
D . 4
 B . 2
C .
B . 2
C .  D . 4
D . 4
设向量  ,若(
,若(  +
+  )∥
)∥  ,则实数k=.
,则实数k=.
 ,若(
,若(  +
+  )∥
)∥  ,则实数k=.
,则实数k=.
若复数z满足: , 则( )
, 则( )
 , 则( )
, 则( )
A . z的实部为3
B . z的虚部为1
C .  D . z在复平面上对应的点位于第一象限
D . z在复平面上对应的点位于第一象限
 D . z在复平面上对应的点位于第一象限
D . z在复平面上对应的点位于第一象限
记等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,
,![]() ,则
,则![]() ____.
____.
函数f(x)=ex+x﹣2的零点所在的一个区间是( )
A.(﹣2,﹣1) B.(﹣1,0) C.(0,1) D.(1,2)
在区间![]() 上随机取一个
上随机取一个![]() ,则
,则![]() 的值介于
的值介于![]() 与
与![]() 之间的概率为 ( )
之间的概率为 ( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
已知集合 2,
2, ,
, ,则
,则

A. B.
B.  C.
C.  D.
D. 
A.
最近更新
- 如图,△ABC是等边三角形,D是AB边上的一点,以CD为边作等边三角形CDE,使点E、A在直线DC的同侧,连接AE.求证
- 在2010年广州亚运会男子百米决赛中,中国运动员劳义的成绩是10秒24,力压群雄成为亚洲“百米飞人”,他全程的平均速度为
- 简述结论,并画图说明. 直线a在平面α内,直线b与直线a相交,则直线b与平面α的位置关系如何?
- Expo’99 Kunming hosted by the Chinese Governmentbetween May
- 已知,则的取值范围是 .
- 在下图所示的实验电路中,两个烧瓶完全相同,用两个相同的电热丝给质量相同的物质A和B加热,实验记录表如下:时间/min 0
- 设NA为阿伏加德罗常数,下列说法正确的是 ( ) A.1.8g 重水(D2O) 含
- 假定英语课上老师要求同桌之间交换修改作文,请你修改你同桌写的以下作文。文中共有10处语言错误,每句中最多两
- 下列成语所反映的情景中,属于光的折射现象的是( ) A.镜ong花水月 B.坐井观天 C.立竿见影
- 如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机取一个点Q,则 点Q取自△ABE内部的概率等于
- 类推是一种重要的化学思维方法,下列推理合理的是() A.碱溶液呈碱性,所以呈碱性的溶液一定都是碱溶液 B.氧化物含有氧元
- 某化学实验小组做了如图实验,请回答以下问题.(1)图A所示实验可观察到“铁树”上浸有无色酚酞试液的棉团由白色变为红色,该
- He is always________ late.A. works B.working C.wo
- 列宁主义被誉为“帝国主义和无产阶级革命时代的马克思主义”,下列各项中不属于列宁开创性理论探索的是
- 8.阅读下文,完成小题 中国职业教育的先驱——黄炎培 1903年春,川沙小学举行开学典礼,这是黄炎培教育生涯的发端。作为
- A、B是一条电场线上的两个点,一带负电的微粒仅在电场力作用下以一定初速度从A点沿电场线运动到B点,其速度—时间图象如图
- 有关细胞呼吸的下列说法中,错误的是: ( ) A.通过有氧呼吸分解等质量的糖元和脂肪,后者产生
- 下面的句子翻译不正确的一项是( ) A.时矫首而遐观(举,抬)善万物之得时。 译文:羡慕自然界的一切生物及
- 在实验室里不宜长期放置,应在使用时新配制的溶液的是: ① 酚酞试剂 ② 银氨溶液 ③ Na2CO3溶液 ④ 氢氧化
- 在不同情况下测得A(g)+3B(g)⇌2C(g)+2D(g)的下列反应速率,其中反应速率最大的是()A. υ(D)=0.



