高中 数学
若集合 , 则集合
, 则集合 中的元素的个数为( )
中的元素的个数为( )
 , 则集合
, 则集合 中的元素的个数为( )
中的元素的个数为( )
A . 5
B . 4
C . 3
D . 2
向量  在向量
在向量  方向上的投影为.
方向上的投影为.
 在向量
在向量  方向上的投影为.
方向上的投影为.
设  它们的大小关系是( )
它们的大小关系是( )
 它们的大小关系是( )
它们的大小关系是( )
A . c<a<b
B . a<c<b
C . b<a<c
D . c<b<a
已知命题  ,
,  ;命题
;命题  若
若  ,则
,则  ,下列命题为真命题的是( )
,下列命题为真命题的是( )
 ,
,  ;命题
;命题  若
若  ,则
,则  ,下列命题为真命题的是( )
,下列命题为真命题的是( )
A .  B .
B .  C .
C .  D .
D . 
为了了解初中生的身体素质,某地区随机抽取了  名学生进行跳绳测试,根据所得数据画样本的频率分布直方图如图所示,且从左到右第一小组的频数是100,则
名学生进行跳绳测试,根据所得数据画样本的频率分布直方图如图所示,且从左到右第一小组的频数是100,则 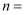 .
.
 名学生进行跳绳测试,根据所得数据画样本的频率分布直方图如图所示,且从左到右第一小组的频数是100,则
名学生进行跳绳测试,根据所得数据画样本的频率分布直方图如图所示,且从左到右第一小组的频数是100,则 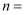 .
. 
下列框图中,可作为流程图的是( )
A .  B .
B .  C .
C .  D .
D . 

已知角θ的终边过点P(1,﹣2),则sinθ=.
已知点P的坐标为 , 点Q是参数方程为
, 点Q是参数方程为 (
(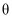 为参数)的椭圆C上的动点,
为参数)的椭圆C上的动点,
 , 点Q是参数方程为
, 点Q是参数方程为 (
(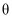 为参数)的椭圆C上的动点,
为参数)的椭圆C上的动点,
-
(1) 求椭圆C的离心率;
-
(2) 求
 的最大值.
的最大值.
某校300名高三学生期中考试数学成绩的频率分布直方图如图所示,由图中数据估计此次数学成绩平均分( )
A . 69
B . 71
C . 73
D . 75
已知函数 , 若
, 若 , 则称实数
, 则称实数 为
为 的“不动点”,若
的“不动点”,若 , 则称实数
, 则称实数 为
为 的“稳定点”,函数
的“稳定点”,函数 的“不动点”和“稳定点”组成的集合分别记为A和B,即
的“不动点”和“稳定点”组成的集合分别记为A和B,即 ,
,  .
.
 , 若
, 若 , 则称实数
, 则称实数 为
为 的“不动点”,若
的“不动点”,若 , 则称实数
, 则称实数 为
为 的“稳定点”,函数
的“稳定点”,函数 的“不动点”和“稳定点”组成的集合分别记为A和B,即
的“不动点”和“稳定点”组成的集合分别记为A和B,即 ,
,  .
.
-
(1) 已知函数
 , 分别求出函数
, 分别求出函数 对应的集合A和B;
对应的集合A和B;
-
(2) 设
 , 若
, 若 , 求函数
, 求函数 对应的集合B.
对应的集合B.
已知等差数列{an}的前n项和为Sn , 公差d≠0,且S3+S5=50,a1 , a4 , a13成等比数列.
-
(1) 求数列{an}的通项公式;
-
(2) 设
 ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
已知圆  ,直线
,直线  .若直线
.若直线  上存在点M,以M为圆心且半径为1的圆与圆C有公共点,则a的取值范围( )
上存在点M,以M为圆心且半径为1的圆与圆C有公共点,则a的取值范围( )
 ,直线
,直线  .若直线
.若直线  上存在点M,以M为圆心且半径为1的圆与圆C有公共点,则a的取值范围( )
上存在点M,以M为圆心且半径为1的圆与圆C有公共点,则a的取值范围( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
函数 的最大值为( )
的最大值为( )
 的最大值为( )
的最大值为( )
A .  B .
B . 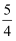 C .
C .  D .
D . 
 B .
B . 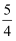 C .
C .  D .
D . 
函数  的图象可由函数
的图象可由函数  的图象至少向右平移( )个单位长度得到.
的图象至少向右平移( )个单位长度得到.
 的图象可由函数
的图象可由函数  的图象至少向右平移( )个单位长度得到.
的图象至少向右平移( )个单位长度得到.
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在①  ;②“
;②“ “是“
“是“ ”的充分不必要条件;③
”的充分不必要条件;③ 这三个条件中任选一个,补充到本题第(2)问的横线处,求解下列问题.
这三个条件中任选一个,补充到本题第(2)问的横线处,求解下列问题.
 ;②“
;②“ “是“
“是“ ”的充分不必要条件;③
”的充分不必要条件;③ 这三个条件中任选一个,补充到本题第(2)问的横线处,求解下列问题.
这三个条件中任选一个,补充到本题第(2)问的横线处,求解下列问题.
问题:已知集合 .
.
-
(1) 当
 时,求A∪B;
时,求A∪B;
-
(2) 若_________,求实数a的取值范围.
已知![]() 则关于
则关于![]() 的方程
的方程![]() 有实根的概率是 ( )
有实根的概率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
如图所示,在正方体ABCD—A1B1C1D1中,E是上底面中心,则AC1与CE的位置关系是( )
A.平行
B.相交
C.相交且垂直
D.以上都不是
某校为了解高一年级学生的数学学科发展状况,随机抽取了100名学生,列出他们的高一第二学期期中考试数学成绩的频率分布直方图如图,其中成绩的分组区间为:[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中a的值;
(2)利用样本估计总体的方法,估计该校高一年级此次期中考试的平均分(同一分组的成绩用该组区间的中点值做代表);
(3)若将分数从高分到低分排列,取前20%的同学评定为“优秀”档次,用样本估计总体的方法,估计本次期中考试“优秀”档次的分数线.

已知三个月球探测器![]() ,
,![]() ,
,![]() 共发回三张月球照片
共发回三张月球照片![]() ,
,![]() ,
,![]() ,每个探测器仅发回一张照片.甲说:照片
,每个探测器仅发回一张照片.甲说:照片![]() 是
是![]() 发回的;乙说:
发回的;乙说:![]() 发回的照片不是
发回的照片不是![]() 就是
就是![]() ;丙说:照片
;丙说:照片![]() 不是
不是![]() 发回的.若甲、乙、丙三人中有且仅有一人说法正确,则照片
发回的.若甲、乙、丙三人中有且仅有一人说法正确,则照片![]() 是探测器_____发回的.
是探测器_____发回的.
若集合
 Z
Z 中有且只有一个元素,则正实数
中有且只有一个元素,则正实数 的取值范围是________
的取值范围是________
最近更新
- 根据下列实验现象可以判断某溶液一定呈碱性的是A.常温下,测得溶液的pH<7 B.溶液中滴入酚酞显红色 C.溶液中滴入石蕊
- 下列各句使用的成语,恰当的一项是 ( )
- 仿照下面例句的形式,选择新的叙述对象,另写两个句子。(6分)例句:⑴折射反射成七彩,可以说,彩虹是备受挫折的阳光;⑵千锤
- 信息归纳;请仔细阅读下面内容,根据所提供的信息完成信息卡。 A New Kind of Hero In the Olym
- 硅肺是矿工中有一种常见的职业病,发病原因是肺部吸入硅尘后,吞噬细胞会吞噬硅尘,却不能产生分解硅尘的酶。硅尘进入体内可破坏
- 杨树的根吸收水分的主要部位是() A.根冠 B.分生区 C.伸长区
- 亚、非两洲都缺失的气候类型是 A.热带雨林气候 B. 温带海洋性气候 C. 地中海气候 D.高山
- Who are these people with banners? -A group _____ itself the
- She let out a s______ at the sight of the little mouse.
- Law r_________ everyone should pay the tax.
- 下列关于叶绿体和光合作用的描述中,正确的是 A.叶片反射绿光故呈绿色,因此日光中绿光透过叶绿体的比例最小 B.叶绿体的类
- Sam _____ some knowledge of the computer just by watching ot
- 设NA表示阿伏加德罗常数的值,下列说法正确的是( ) A.5.6 g Fe和足量的盐酸完全反应失去电子数为0.3 N
- 容积固定的密闭容器中,发生可逆反应:M(g)+N(g) 2P(g)+Q(g) ΔH>0, 请回答下列问题: (1)在某
- 右图A、B是等体积容器,K是开关,活塞可以左右移动。在一定温度下,关闭K,向A中通入一定量的NO2。发生:2NO2(g)
- 下列投资理财方式中包含着债权和债务关系的是() ①购买股票 ②购买国债 ③存款储蓄 ④持有汇票 A.①② B.②③
- 下面关于蛋白质分子结构与功能的叙述,错误的是() A.不同蛋白质含有的氨基酸数量不尽相同 B.有些结构不同的蛋白质具有相
- 将的油酸溶于酒精,制成的油酸酒精溶液,已知的溶液有50滴,现取1滴油酸酒精溶液滴到水面上,随着酒精溶于水,油酸在水面上形
- 对于在密闭容器中进行的反应:N2+O2 2NO,下列不能加快该反应的反应速率的条件是 A.体积增大到原的2倍
- 小丽同用连线的方式对某一主题知识进行如下归纳,其中有错误的一组是 A性质与用途: 天然最硬的物质——镶玻璃刀头 熟石



