高中 数学
已知函数  是定义在
是定义在  上的偶函数,且当
上的偶函数,且当  时,
时,  单调递增,则关于x的不等式
单调递增,则关于x的不等式  的解集为 ( )
的解集为 ( )
 是定义在
是定义在  上的偶函数,且当
上的偶函数,且当  时,
时,  单调递增,则关于x的不等式
单调递增,则关于x的不等式  的解集为 ( )
的解集为 ( )
A .  B .
B .  C .
C . 
 D . 随a的值而变化
D . 随a的值而变化
 B .
B .  C .
C . 
 D . 随a的值而变化
D . 随a的值而变化
已知双曲线 , 过左焦点
, 过左焦点 且斜率为
且斜率为 的直线交
的直线交 的一条渐近线于点
的一条渐近线于点 , 且
, 且 在第一象限,若
在第一象限,若 (
( 为坐标原点),则
为坐标原点),则 的渐近线方程为.
的渐近线方程为.
 , 过左焦点
, 过左焦点 且斜率为
且斜率为 的直线交
的直线交 的一条渐近线于点
的一条渐近线于点 , 且
, 且 在第一象限,若
在第一象限,若 (
( 为坐标原点),则
为坐标原点),则 的渐近线方程为.
的渐近线方程为.
在  中,若
中,若  ,则
,则  与
与  的关系为( )
的关系为( )
 中,若
中,若  ,则
,则  与
与  的关系为( )
的关系为( )
A . 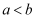 B .
B .  C .
C .  D .
D . 
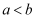 B .
B .  C .
C .  D .
D . 
若[x]表示不超过x的最大整数,如[2.1]=2,[﹣2.1]=﹣3.执行如图所示的程序框图,则输出的S值为( )

A . 2
B . 3
C . 4
D . 5
自来水厂一蓄水池可以用甲、乙两个水泵注水,单开甲泵需15小时注满,单开乙泵需18小时注满,若要求10小时注满水池,并且使两泵同时开放的时间尽可能地少,则甲、乙两水泵同时开放的时间最少需( )
A . 4小时
B . 7小时
C . 6小时
D . 14小时
已知  ,则
,则 
 ,则
,则 
若复数z满足  ,则在复平面内z对应的点的坐标是( )
,则在复平面内z对应的点的坐标是( )
 ,则在复平面内z对应的点的坐标是( )
,则在复平面内z对应的点的坐标是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
关于奇函数与偶函数,以下说法正确的是:( )
A . 任何函数都可以表示成一个偶函数与一个奇函数的和;
B . 任何函数都可以表示成一个偶函数与一个奇函数的差;
C . 任何函数都可以表示成一个偶函数与一个奇函数的和,并且这种表示方法不唯一;
D . 有些函数不能表示成一个偶函数与一个奇函数之和
已知集合P,Q 为非空集合,定义集合P+Q={a+b|a∈P,b∈Q},若P={0,2,5},Q={1,2,6},则P+Q中元素个数共有( )
A . 9个
B . 8个
C . 7个
D . 6个
函数 所有零点的和等于( )
所有零点的和等于( )
 所有零点的和等于( )
所有零点的和等于( )
A . 6
B . 7.5
C . 9
D . 12
 ,
,  ,
,  .
.
-
(1) 当
 时,求
时,求  的
的  的取值范围;
的取值范围;
-
(2) 解关于
 的不等式
的不等式  的解集;
的解集;
-
(3) 对于任意的
 ,
,  恒成立,求
恒成立,求  的取值范围.
的取值范围.
已知  为锐角,且
为锐角,且  ,则
,则  ( )
( )
 为锐角,且
为锐角,且  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数  ,
,  .
.
 ,
,  .
.
-
(1) 当k=0时,函数g(x)的零点个数为;
-
(2) 若函数g(x)恰有2个不同的零点,则实数k的取值范围为.
如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,AB⊥AC,且AB=1,BC=2,PA⊥底面ABCD,PA=  ,又E为边BC上异于B,C的点,且PE⊥ED.
,又E为边BC上异于B,C的点,且PE⊥ED.
 ,又E为边BC上异于B,C的点,且PE⊥ED.
,又E为边BC上异于B,C的点,且PE⊥ED. 
-
(1) 求证:平面PAE⊥平面PDE;
-
(2) 求点A到平面PDE的距离.
利用数学归纳法证明不等式  的过程中,由
的过程中,由  变成
变成  时,左边增加了( )
时,左边增加了( )
 的过程中,由
的过程中,由  变成
变成  时,左边增加了( )
时,左边增加了( )
A . 1项
B .  项
C .
项
C .  项
D .
项
D .  项
项
 项
C .
项
C .  项
D .
项
D .  项
项
已知数列  满足:
满足:  ,
, 
 满足:
满足:  ,
, 
-
(1) 求数列
 的通项公式;
的通项公式;
-
(2) 若数列
 满足:
满足:  ,证明:
,证明:  是等差数列.
是等差数列.
-
(3) 证明:
 .
.
天气转暖,太阳辐射增强,遮阳帽比较畅销,某商家为了解某种遮阳帽如何定价可以获得最大利润,现对这种遮阳帽进行试销售.统计后得到其单价x(单位:元)与销量y(单位:顶)的相关数据如表:
单价x(元/顶) | 30 | 35 | 40 | 45 | 50 |
日销售量y(顶) | 140 | 130 | 110 | 90 | 80 |
附:对于一组数据(x1 , y1),(x2 , y2),…,(xn,yn),其回归直线 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
, 
参考数据:
-
(1) 已知销量y与单价x具有线性相关关系,求y关于x的线性回归方程;
-
(2) 若每顶帽子的成本为25元,试销售结束后,请利用(1)中所求的线性回归方程确定单价为多少元时,销售利润最大?(结果保留到整数).
在长方体![]() 中,
中,![]() ,
,![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的余弦值为______.
所成角的余弦值为______.
.若函数 则
则![]() = ()
= ()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
已知函数 ,则
,则
A. 在(0,2)单调递增 B.
在(0,2)单调递增 B.  在(0,2)单调递减
在(0,2)单调递减
C. 的图像关于直线x=1对称 D.
的图像关于直线x=1对称 D.  的图像关于点(1,0)对称
的图像关于点(1,0)对称
A.
C.
最近更新
- 下列图中动植物糖类、脂质的种类与比较正确的是( )
- 在水平光滑的细直角槽中嵌入两个质量相等的小物体A和B,如图所示,它们之间用一长为L、质量可以忽略的刚性细杆铰接,铰接处在
- 在烧瓶里放少量的碘,并用酒精灯对烧杯微微加热,过一会儿停止加热。在此实验中可以看到,固态的碘没有熔化,而直接变成紫色的碘
- (14分)A、B、C、D四种可溶的化合物(所含离子各不相同),分别由阳离子Na+、Mg2+、Al3+、Ba2+和阴离子两
- 某名贵花卉用种子繁殖会发生性状分离。为了防止性状分离并快速繁殖,可以利用该植物的一部分器官或组织进行离体培养,发育出完整
- 在某生态系统中,存在蛇、猫头鹰和鼠等动物。当猫头鹰也以鼠为食时,蛇与鼠、蛇与猫头鹰的关系是: ( )A.捕
- 关于哲学和世界观的关系,下列表述中正确的是() ①世界观是人们对整个世界以及人与世界关系的总的看法和根本观点 ②哲学就是
- 材料一:日月星辰总是按照一定轨道运转;电子总是按照一定秩序排布在原子核外,绕原子核运转。 材料二:大雁冬天南飞,春天北返
- Along with his letter was his promise he would atte
- 如图,直角梯形ABCD中,AD∥BC,∠B=90°,BC=2AB=2AD=4.以AB为直径作⊙O,点P在梯形内的半圆弧上
- 2010年南非世界杯期间,章鱼哥保罗已经预测了8场比赛,命中率100%。球迷们是看结果的,不是看唯心主义怎样战胜唯物主义
- 下列说法正确的是( ) A. 二氧化硫可以使溴水褪色是因为它有漂白性 B. 浓硫酸可用于干燥H2S和CO2 C.
- 已知B港口位于A观测点的东北方向,且其到A观测点正北方向的距离BD的长为16千米,一艘货轮从B港口以48千米/时的速度沿
- 请对下列病句提出修改意见 (1)上课时只有集中精力听讲、认真思考,就能把握学习重点,提高学习效率。 修改意见: (2)欢
- 已知一个直角三角形的两边长分别为3和4,则第三边长的平方是() A.25 B.14 C.7D.7或2
- 根据提示, 利用本单元所学知识, 完成下面的小作文。 1. 众所周知, 在中国, 许多青少年养成了吸烟的习惯。(as定语
- 如果一个氨基酸分子中有两个羧基,其中一个羧基连接在R基上,那么另一羧基的部位是在 A、与氨基端相连
- 双隔膜电解池的结构示意简图如图所示,对该装置及其原理判断错误的是 () A. c隔膜为阴离子交换膜、d隔膜为阳离子交换膜
- 上海世博会要确保成功、精彩、难忘,除了场馆建设、布展、文化活动等内容外,上海干部能否在言谈举止等各方面体现良好与素养也非
- 如图,一个放置在水平桌面上的圆柱,它的主(正)视图是



