木板滑块模型 知识点题库
如图所示,质量为3m的木板静止在光滑的水平面上,一个质量为2m的物块(可视为质点),静止在木板上的A端,已知物块与木板间的动摩擦因数为μ.现有一质量为m的子弹(可视为质点)以初速度v0水平向右射入物块并穿出,已知子弹穿出物块时的速度为  ,子弹穿过物块的时间极短,不计空气阻力,重力加速度为g.求:
,子弹穿过物块的时间极短,不计空气阻力,重力加速度为g.求:
 ,子弹穿过物块的时间极短,不计空气阻力,重力加速度为g.求:
,子弹穿过物块的时间极短,不计空气阻力,重力加速度为g.求:
①子弹穿出物块时物块的速度大小.
②子弹穿出物块后,为了保证物块不从木板的B端滑出,木板的长度至少多大?
如图所示,小车M处在光滑水平面上,其上表面粗糙,靠在(不粘连)半径为R=0.2m的  光滑固定圆弧轨道右侧,一质量m=1 kg的滑块(可视为质点)从A点正上方H=3m处自由下落经圆弧轨道底端B滑上等高的小车表面。滑块在小车上最终未离开。已知小车质量M=3kg,滑块与小车间的动摩擦因数μ=0.2。(取g=10 m/s2),求:
光滑固定圆弧轨道右侧,一质量m=1 kg的滑块(可视为质点)从A点正上方H=3m处自由下落经圆弧轨道底端B滑上等高的小车表面。滑块在小车上最终未离开。已知小车质量M=3kg,滑块与小车间的动摩擦因数μ=0.2。(取g=10 m/s2),求:
 光滑固定圆弧轨道右侧,一质量m=1 kg的滑块(可视为质点)从A点正上方H=3m处自由下落经圆弧轨道底端B滑上等高的小车表面。滑块在小车上最终未离开。已知小车质量M=3kg,滑块与小车间的动摩擦因数μ=0.2。(取g=10 m/s2),求:
光滑固定圆弧轨道右侧,一质量m=1 kg的滑块(可视为质点)从A点正上方H=3m处自由下落经圆弧轨道底端B滑上等高的小车表面。滑块在小车上最终未离开。已知小车质量M=3kg,滑块与小车间的动摩擦因数μ=0.2。(取g=10 m/s2),求: 
-
(1) 滑块通过A点时滑块受到的弹力大小和方向
-
(2) 小车M的最小长度
在水平面上有一个长度为L=2m、质量为M=1kg的木板P,在木板上正中央放置一个质量为m=2kg的小滑块Q,PQ之间动摩擦因数为μ1=0.2,P与水平面之间动摩擦因数为μ2=0.4,系统静止.取g=10m/s2
![]()
-
(1) 若对Q施加一个水平向右的恒力F=16N,欲使Q从P上掉下去,求F对Q至少要做多少功;
-
(2) 若对P施加一个水平向右的恒力F=15N,欲使Q从P上掉下去,求F最短作用时间。
如图所示,质量为M且足够长的木板静止在光滑水平面上,木板的右侧有一墙壁。一质量为m的物块以速度v0由木板左侧滑上木板,已知木板与物块质量关系为M = 3m,物块与木板间的动摩擦因数为μ,重力加速度为g,木板与墙壁碰撞不损失动能。
![]()
-
(1) 若它们达到共同速度后木板跟墙壁发生碰撞并反弹运动,最终物块能在木板上滑行多少距离
-
(2) 若要求木板与墙壁能发生第二次碰撞,木板右侧与墙壁间的距离
 应满足什么条件
应满足什么条件
如图所示,在光滑水平面上有B、C两个木板,B的上表面光滑,C的上表面粗糙,B上有一个可视为质点的物块A,A、B、C的质量分别为3m、2m、m.A、B以相同的初速度v向右运动,C以速度v向左运动.B、C的上表面等高,二者发生完全非弹性碰撞但并不粘连,碰撞时间很短.A滑上C后恰好能到达C的中间位置,C的长度为L,不计空气阻力.求:
![]()
-
(1) 木板C的最终速度;
-
(2) 木板C与物块A之间的摩擦力f;
-
(3) 物块A滑上木板C之后,在木板C上做减速运动的时间t.
如图所示,质量为M的长木板静置于光滑水平面上,一质量为m的小铅块(可视为质点)以水平初速vo由木板左端滑上木板,铅块滑至木板的右端时恰好与木板相对静止,此时,它们共同的速度为v  ,已知铅块与长木块间的动摩擦因数为μ,木板长为
,已知铅块与长木块间的动摩擦因数为μ,木板长为  ,在此过程中,木板前进的距离为s,则在这个过程中产生的热量等于( )
,在此过程中,木板前进的距离为s,则在这个过程中产生的热量等于( )
 ,已知铅块与长木块间的动摩擦因数为μ,木板长为
,已知铅块与长木块间的动摩擦因数为μ,木板长为  ,在此过程中,木板前进的距离为s,则在这个过程中产生的热量等于( )
,在此过程中,木板前进的距离为s,则在这个过程中产生的热量等于( ) 
A . μmgs
B . μmg(s+  )
C . μmg
)
C . μmg  D .
D .  mv
mv  ﹣
﹣  (m+M)v
(m+M)v 
 )
C . μmg
)
C . μmg  D .
D .  mv
mv  ﹣
﹣  (m+M)v
(m+M)v 
下暴雨时,有时会发生山体滑坡或泥石流等地质灾害.某地有一倾角为θ=37°(sin37°=  )的山坡C,上面有一质量为m的石板B,其上下表面与斜坡平行;B上有一碎石堆A(含有大量泥土),A和B均处于静止状态,如图所示.假设某次暴雨中,A浸透雨水后总质量也为m(可视为质量不变的滑块),在极短时间内,A、B间的动摩擦因数μ1减小为
)的山坡C,上面有一质量为m的石板B,其上下表面与斜坡平行;B上有一碎石堆A(含有大量泥土),A和B均处于静止状态,如图所示.假设某次暴雨中,A浸透雨水后总质量也为m(可视为质量不变的滑块),在极短时间内,A、B间的动摩擦因数μ1减小为  ,B、C间的动摩擦因数μ2减小为0.5,A、B开始运动,此时刻为计时起点;在第2s末,B的上表面突然变为光滑,μ2保持不变.已知A开始运动时,A离B下边缘的距离l=27m,C足够长,设最大静摩擦力等于滑动摩擦力.取重力加速度大小g=10m/s2 . 求:
,B、C间的动摩擦因数μ2减小为0.5,A、B开始运动,此时刻为计时起点;在第2s末,B的上表面突然变为光滑,μ2保持不变.已知A开始运动时,A离B下边缘的距离l=27m,C足够长,设最大静摩擦力等于滑动摩擦力.取重力加速度大小g=10m/s2 . 求:

-
(1) 在0~2s时间内A和B加速度的大小;
-
(2) A在B上总的运动时间.
如图甲所示,质量  的粗糙长木板P(足够长)静止在水平地面上,一个可视为质点的物块Q以初速度
的粗糙长木板P(足够长)静止在水平地面上,一个可视为质点的物块Q以初速度  滑上长木板上表面,在物块Q滑上长木板P的同时给P施加个方向水平向右大小为
滑上长木板上表面,在物块Q滑上长木板P的同时给P施加个方向水平向右大小为  的拉力
的拉力  ,P、Q的
,P、Q的 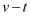 图线如图乙所示,其中
图线如图乙所示,其中  、
、  段分别是
段分别是 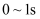 内Q、P的
内Q、P的 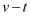 图线,
图线,  段是
段是  内P、Q共同的
内P、Q共同的 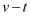 图线,最大静摩擦力等于滑动摩擦力,
图线,最大静摩擦力等于滑动摩擦力, 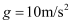 ,下列说法正确的是( )
,下列说法正确的是( )
 的粗糙长木板P(足够长)静止在水平地面上,一个可视为质点的物块Q以初速度
的粗糙长木板P(足够长)静止在水平地面上,一个可视为质点的物块Q以初速度  滑上长木板上表面,在物块Q滑上长木板P的同时给P施加个方向水平向右大小为
滑上长木板上表面,在物块Q滑上长木板P的同时给P施加个方向水平向右大小为  的拉力
的拉力  ,P、Q的
,P、Q的 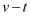 图线如图乙所示,其中
图线如图乙所示,其中  、
、  段分别是
段分别是 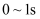 内Q、P的
内Q、P的 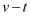 图线,
图线,  段是
段是  内P、Q共同的
内P、Q共同的 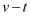 图线,最大静摩擦力等于滑动摩擦力,
图线,最大静摩擦力等于滑动摩擦力, 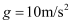 ,下列说法正确的是( )
,下列说法正确的是( ) 
A . 物块Q的质量为  B . P、Q之间的动摩擦因数为0.4,P与地面间的动摩擦因数为0.2
C . 长木板P最小的长度为
B . P、Q之间的动摩擦因数为0.4,P与地面间的动摩擦因数为0.2
C . 长木板P最小的长度为  D .
D . 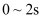 内物块Q的位移大小为
内物块Q的位移大小为 
 B . P、Q之间的动摩擦因数为0.4,P与地面间的动摩擦因数为0.2
C . 长木板P最小的长度为
B . P、Q之间的动摩擦因数为0.4,P与地面间的动摩擦因数为0.2
C . 长木板P最小的长度为  D .
D . 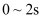 内物块Q的位移大小为
内物块Q的位移大小为 
如图所示,学校物理实验室里,需要将一张大实验桌移动一段距离。现有质量  的实验桌放置在水平地面上,实验桌的水平台面离地高度
的实验桌放置在水平地面上,实验桌的水平台面离地高度  ,它与水平地面的动摩擦因数
,它与水平地面的动摩擦因数  ,另有一质量
,另有一质量  的金属块(可视为质点)置于实验桌上,它到实验桌尾的距离
的金属块(可视为质点)置于实验桌上,它到实验桌尾的距离  ,与实验桌桌面间的动摩擦因数
,与实验桌桌面间的动摩擦因数  。今对实验桌施加一个水平向右的恒定拉力,使其开始运动,一段时间后物块从桌面上滑落,刚滑落时,实验桌已向右行进了距离
。今对实验桌施加一个水平向右的恒定拉力,使其开始运动,一段时间后物块从桌面上滑落,刚滑落时,实验桌已向右行进了距离  。求:
。求:
 的实验桌放置在水平地面上,实验桌的水平台面离地高度
的实验桌放置在水平地面上,实验桌的水平台面离地高度  ,它与水平地面的动摩擦因数
,它与水平地面的动摩擦因数  ,另有一质量
,另有一质量  的金属块(可视为质点)置于实验桌上,它到实验桌尾的距离
的金属块(可视为质点)置于实验桌上,它到实验桌尾的距离  ,与实验桌桌面间的动摩擦因数
,与实验桌桌面间的动摩擦因数  。今对实验桌施加一个水平向右的恒定拉力,使其开始运动,一段时间后物块从桌面上滑落,刚滑落时,实验桌已向右行进了距离
。今对实验桌施加一个水平向右的恒定拉力,使其开始运动,一段时间后物块从桌面上滑落,刚滑落时,实验桌已向右行进了距离  。求:
。求: 
-
(1) 物块在实验桌上滑动的时间及对实验桌所施加的恒力
 的大小;
的大小;
-
(2) 物块落地时,落地点至实验桌边的水平距离
 。
。
如图甲所示,光滑水平面上停有一块质量为  的长木板,其长度
的长木板,其长度  。有一个质量为
。有一个质量为 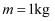 的物块(可视为质点) 从长木板的左端以
的物块(可视为质点) 从长木板的左端以  的速率冲上长木板,已知物块与长木板之间的动摩擦因数
的速率冲上长木板,已知物块与长木板之间的动摩擦因数  ,取
,取  。
。
 的长木板,其长度
的长木板,其长度  。有一个质量为
。有一个质量为 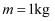 的物块(可视为质点) 从长木板的左端以
的物块(可视为质点) 从长木板的左端以  的速率冲上长木板,已知物块与长木板之间的动摩擦因数
的速率冲上长木板,已知物块与长木板之间的动摩擦因数  ,取
,取  。
。 

-
(1) 物块滑上长木板时,长木板的加速度大小;
-
(2) 试判断:物块冲上长木板后能否从其右端滑出?若能滑出,求物块滑离长木板时的速率;若不能滑出,求物块与长木板相对静止时的速率;
-
(3) 若在长木板的上表面铺上一种特殊材料,其动摩擦因数μ与物块到长木板左端距离x关系如图乙所示。物块仍以相同速率从左端冲上长木板后,要使物块能从长木板的右端滑出,则长木板的长度应满足什么条件?
如图所示,倾角为37°的光滑斜面与半径为R的光滑圆弧轨道相切于B点,质量为2m、长为L=6.4R的小车静止在光滑水平面上,左端靠在圆弧轨道最低点C处,距车右端S处有一固定挡板,挡板距车右端的距离S可调,挡板上固定直径为R的光滑半圆轨道DEG,小车的上表面与C、D的连线在同一水平面内。质量为m的物块从斜面上的A点静止释放,滑上小车后带动小车运行,小车与挡板碰撞后立即被挡板牢固粘连。物块与小车间的动摩擦因数μ=0.5,A、B两点间的竖直高度h=4.3R,重力加速度为g,物块视为质点,空气阻力不计,sin37°=0.6,cos37°=0.8。

-
(1) 求物块到达C处时对圆弧轨道的压力;
-
(2) 要使物块与小车达到共同速度时车刚好与挡板相撞,S取多少?
-
(3) 求物块从滑上小车到刚离开小车的过程中,物块克服摩擦力做的功Wf与S的大小关系,并判断S取不同值时物块能否到达半圆弧的中点E处。
如图所示,A点距水平面BC的高度h=1.25m,BC与圆弧轨道CDE相接于C点,D为圆弧轨道的最低点,圆弧轨道DE对应的圆心角θ=37°,圆弧的半径R=0.5m,圆弧和倾斜传送带EF相切于E点,EF的长度为l=5m,一质量为m=1kg的小物块从A点以v0=5m/s的速度水平抛出,从C点沿切线进入圆弧轨道,当经过E点时,物体受到圆弧的摩擦力f=40N,随后物块滑上传送带EF,已知物块与圆弧上E点附近以及传送带EF间的动摩擦因数μ均为0.5,重力加速度g=10m/s2 , sin  =0.6,cos
=0.6,cos  =0.8,求:
=0.8,求:
 =0.6,cos
=0.6,cos  =0.8,求:
=0.8,求: 
-
(1) 物块做平抛运动时水平方向的位移BC的长度;
-
(2) 物块到达E处时速度的大小;
-
(3) 若物块能被送到F端,传送带顺时针运转的速度应满足的条件及物块从E端到F端所用时间的范围。
如图所示,两端带有挡板的木板静止放置在粗糙水平面上,木板的质量M=1kg,木板的长度L=12m,木板的上表面光滑,木板与地面之间的动摩擦因数μ=0.1。在木板的中间位置静止放置质量为m的木块,某时刻给木块一水平向右的初速度v0=6m/s当地重力加速度g=10m/s2 , 木块可视为质点,挡板厚度不计。
![]()
-
(1) 若m=1kg,木块与挡板碰撞后粘在一起,木板在地面上滑行的距离x;
-
(2) 若m=0.5kg,木块与挡板发生弹性碰撞求木板运动的总路程s;
-
(3) 若m=2kg,木块与挡板发生弹性碰撞,木块运动的总时间t。
如右图所示,两块木板的质量分别为M1=500g,M2=400g.静止于光滑水平面上,小物块m=100g以初速度为v=10m/s滑上M1的表面,最后停在M2上时速度为  1.5m/s,求:
1.5m/s,求:
 1.5m/s,求:
1.5m/s,求:

-
(1) 最后M1的速度v1
-
(2) m刚离开Ml时的速度

如图所示,物块以一定的初速度滑上原静止光滑水平地面上的长木板,两者达到相同速度v后向右运动,某时刻木板与右方的竖直墙发生碰撞。已知物块质量为木板质量的3倍,物块与木板间的动摩擦因数为μ,重力加速度为g。设定板与墙的碰撞为弹性碰撞,时间极短,并且木板足够长,物块始终在木板上、求:

-
(1) 物块刚滑上木板的初速度v0;
-
(2) 木板与墙第二次碰撞前物块距木板左端的距离L;
-
(3) 木板从第一次与墙碰撞到第n次与墙碰撞所经历的总时间t。
如图所示,木块(视为质点)的质量  与长木板静止叠放在光滑的水平面上,木块与木板间的动摩擦因数为
与长木板静止叠放在光滑的水平面上,木块与木板间的动摩擦因数为  ,现在给木块的水平拉力F是木板重力的2倍,则木块、木板刚好要发生相对运动,设最大静摩擦力等于滑动摩擦力,重力加速度为
,现在给木块的水平拉力F是木板重力的2倍,则木块、木板刚好要发生相对运动,设最大静摩擦力等于滑动摩擦力,重力加速度为 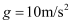 ,下列说法正确的是( )
,下列说法正确的是( )
 与长木板静止叠放在光滑的水平面上,木块与木板间的动摩擦因数为
与长木板静止叠放在光滑的水平面上,木块与木板间的动摩擦因数为  ,现在给木块的水平拉力F是木板重力的2倍,则木块、木板刚好要发生相对运动,设最大静摩擦力等于滑动摩擦力,重力加速度为
,现在给木块的水平拉力F是木板重力的2倍,则木块、木板刚好要发生相对运动,设最大静摩擦力等于滑动摩擦力,重力加速度为 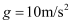 ,下列说法正确的是( )
,下列说法正确的是( ) 
A . 此时木板相对木块有向右运动的趋势
B . 此时整体所受的合力小于F
C . 木板的质量为  D . 此时整体的加速度为
D . 此时整体的加速度为 
 D . 此时整体的加速度为
D . 此时整体的加速度为 
如图半径为R=0.45m的光滑四分之一圆弧轨道AB下端B点与光滑水平面CD形成一个高为h=0.2m的台阶,一质量为M=0.2kg的平板小车静止在光滑水平面上紧靠台阶,圆弧轨道与平板小车在B点平滑连接。现将一个质量为m=0.2kg的物块(可视为质点)从圆弧轨道顶端A点由静止释放,物块经过圆弧轨道滑上平板小车,经时间t=0.4s滑离平板小车,物块滑离平板小车瞬间的速度是平板小车速度的2倍,物块最终落在光滑平面上D点。g=10m/s2 , 求:

-
(1) 物块与平板小车之间的动摩擦因数μ;
-
(2) 物块滑离平板小车时平板小车移动的距离;
-
(3) 物块落地时,落地点D到平板小车右端的距离。
如图甲所示,在水平地面上有一长木板B,其上叠放木块A,已知最大静摩擦力等于滑动摩擦力。用一水平力F作用于B,A、B的加速度与F的关系如图乙所示,重力加速度g取10m/s2 , 则下列说法中正确的是( )

A . A的质量为0.5kg
B . B的质量为1.25kg
C . B与地面间的动摩擦因数为0.2
D . A,B间的动摩擦因数为0.2
如图所示,质量为m=1kg的滑块和质量为M=2kg的滑板叠放在一起,滑块与滑板之间的动摩擦因数μ1=0.1,滑板与地面之间的动摩擦因数为μ2=0.2,某时刻滑板滑块恰好以相同的速度向右运动,此时给木板施加向右的恒力F,若要求滑板滑块在往后的运动中不相对滑动,F的值可能为( )

A . 0N
B . 4N
C . 6N
D . 10N
如图甲所示,一滑块置于足够长的长木板左端木板放置在水平地面上。已知滑块和木板的质量均为2kg,现在滑块上施加一个F=0.5t (N)的变力,从t=0时刻开始计时,滑块所受摩擦力随时间变化的关系如图乙所示。设最大静摩擦力与滑动摩擦力相等,重力加速度g取10m/s2求:

-
(1) 木板与水平地面间的动摩擦因数;
-
(2) 滑块与木板间的动摩擦因数;
-
(3) t2 时刻木板的速度大小。
最近更新
- 已知丙二醇的结构简式为,下列关于丙二醇的
- 下列词语中没有错别字的一项是 ( )
- 下列叙述正确的是 A.NH3是极性分子,分子中N
- The soldier was ____ of running away when the enemy attacked
- You should come to school ____________.A.in timeB.on tim
- The boy _______ on the ground _______ that he had seen a co
- 新疆是一个多民族聚居的地区,在这片广袤的
- 选出下列加点字注音全对的一项( )
- 土地,也许代表故乡、也许代表归宿、也许代
- 设函数则满足的x的取值范围是__________。
- 将抛物线先向左平移2个单位,再向下平移1个
- 黑色人种主要分布在( ) A.亚洲东部和
- 下列生物中属于原核生物的一组是( ) A
- 阿杜的《天黑》异常受FANS们的追捧,尤其其
- 函数y=sin x-2ex的导数为.
- 某种橡胶分解产物为碳氢化合物,对这种碳氢
- 下图是甲、乙两种固体物质在水中的溶解度曲
- 名句默写(任选4小题作答,如全选,则以前4
- 分解因式 ▲ .



