木板滑块模型 知识点题库
如图(a),一长木板静止于光滑水平桌面上, 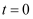 时,小物块以速度
时,小物块以速度 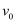 滑到长木板上,
滑到长木板上,  时刻小物块恰好滑至长木板最右端。图(b)为物块与木板运动的
时刻小物块恰好滑至长木板最右端。图(b)为物块与木板运动的 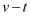 图像,已知图中
图像,已知图中  、
、 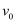 、
、 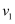 ,重力加速度大小为g。下列说法正确的是( )
,重力加速度大小为g。下列说法正确的是( )
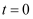 时,小物块以速度
时,小物块以速度 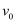 滑到长木板上,
滑到长木板上,  时刻小物块恰好滑至长木板最右端。图(b)为物块与木板运动的
时刻小物块恰好滑至长木板最右端。图(b)为物块与木板运动的 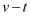 图像,已知图中
图像,已知图中  、
、 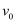 、
、 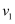 ,重力加速度大小为g。下列说法正确的是( )
,重力加速度大小为g。下列说法正确的是( ) 

A . 木板的长度为  B . 物块与木板的质量之比为
B . 物块与木板的质量之比为  C . 物块与木板之间的动摩擦因数为
C . 物块与木板之间的动摩擦因数为  D . t1时刻,小物块和木板动能之比为
D . t1时刻,小物块和木板动能之比为 
 B . 物块与木板的质量之比为
B . 物块与木板的质量之比为  C . 物块与木板之间的动摩擦因数为
C . 物块与木板之间的动摩擦因数为  D . t1时刻,小物块和木板动能之比为
D . t1时刻,小物块和木板动能之比为 
如图,质量为3 kg的木板放在光滑的水平地面上,质量为1 kg的木块放在木板上,它们之间有摩擦,木板足够长,两者都以4m/s的初速度向相反方向运动.当木板的速度为2.4 m/s时,木块( )

A . 处于匀速运动阶段
B . 处于减速运动阶段
C . 处于加速运动阶段
D . 静止不动
如图所示,一质量为M的长木板静止在水平面上,有一质量为m的小滑块以一定的水平速度冲上木板,已知滑块和木板之间的动摩擦因数为  ,最大静摩擦力等于滑动摩擦力,求
,最大静摩擦力等于滑动摩擦力,求

-
(1) 若滑块在木板上滑动时,木板能保持静止不动,木板和地面之间的动摩擦因数须满足什么条件?
-
(2) 若长木板的质量M=0.2kg,长木板与水平面间的动摩擦因数μ=0.1。滑块的质量也为0.2kg。滑块以v0=1.2m/s的速度滑上长板的左端,小滑块与长木板间的动摩擦因数μ0=0.4。滑块最终没有滑离长木板,求滑块在开始滑上长木板到最后静止下来的过程中,滑块滑行的距离是多少?(g=10m/s2)
如图所示,质量M=8kg的小车静止在光滑水平面上,在小车右端施加一水平拉力F=8N,当小车速度达到v=1.5m/s时,在小车的右端由静止轻放一质量m=2kg的木块(可视为质点),木块与小车间的动摩擦因数μ=0.2,小车足够长,(g取10m/s2)求:

-
(1) 木块相对小车运动的时间;
-
(2) 在1.5秒内木块与小车间产生的热量。
如图所示,质量M=5kg的小车静止在光滑水平地面上,小车左侧AB部分水平,右侧BC部分为半径R=0.5m的竖直光滑  圆弧面,AB与BC恰好在B点相切,CD为竖直侧壁。质量m=1kg的小滑块以v0=6m/s的初速度从小车左端的A点滑上小车,运动到B点时与小车相对静止一起向前运动,之后小车与右侧竖直墙壁发生碰撞,碰撞前后无能量损失。已知滑块与小车AB段间的动摩擦因数μ=0.5,重力加速度g=10m/s2 , 求:
圆弧面,AB与BC恰好在B点相切,CD为竖直侧壁。质量m=1kg的小滑块以v0=6m/s的初速度从小车左端的A点滑上小车,运动到B点时与小车相对静止一起向前运动,之后小车与右侧竖直墙壁发生碰撞,碰撞前后无能量损失。已知滑块与小车AB段间的动摩擦因数μ=0.5,重力加速度g=10m/s2 , 求:
 圆弧面,AB与BC恰好在B点相切,CD为竖直侧壁。质量m=1kg的小滑块以v0=6m/s的初速度从小车左端的A点滑上小车,运动到B点时与小车相对静止一起向前运动,之后小车与右侧竖直墙壁发生碰撞,碰撞前后无能量损失。已知滑块与小车AB段间的动摩擦因数μ=0.5,重力加速度g=10m/s2 , 求:
圆弧面,AB与BC恰好在B点相切,CD为竖直侧壁。质量m=1kg的小滑块以v0=6m/s的初速度从小车左端的A点滑上小车,运动到B点时与小车相对静止一起向前运动,之后小车与右侧竖直墙壁发生碰撞,碰撞前后无能量损失。已知滑块与小车AB段间的动摩擦因数μ=0.5,重力加速度g=10m/s2 , 求: 
-
(1) 小车与墙壁碰撞前的速度大小;
-
(2) 小车AB段的长度;
-
(3) 试通过计算说明:小车与墙壁碰撞后,滑块能否从C点滑出。
如图所示,一足够长的木板在光滑的水平面上以速度 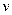 向右匀速运动,现将质量为
向右匀速运动,现将质量为  的物体竖直向下轻轻地放置在木板上的右端,已知物体
的物体竖直向下轻轻地放置在木板上的右端,已知物体  和木板之间的动摩擦因数为
和木板之间的动摩擦因数为 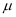 。为保持木板的速度不变,从物体
。为保持木板的速度不变,从物体  放到木板上到它相对木板静止的过程中,须对木板施加一水平向右的作用力
放到木板上到它相对木板静止的过程中,须对木板施加一水平向右的作用力  ,那么力
,那么力  对木板做功的数值为( )
对木板做功的数值为( )
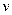 向右匀速运动,现将质量为
向右匀速运动,现将质量为  的物体竖直向下轻轻地放置在木板上的右端,已知物体
的物体竖直向下轻轻地放置在木板上的右端,已知物体  和木板之间的动摩擦因数为
和木板之间的动摩擦因数为 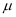 。为保持木板的速度不变,从物体
。为保持木板的速度不变,从物体  放到木板上到它相对木板静止的过程中,须对木板施加一水平向右的作用力
放到木板上到它相对木板静止的过程中,须对木板施加一水平向右的作用力  ,那么力
,那么力  对木板做功的数值为( )
对木板做功的数值为( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
长为  的长木板B静止放在水平冰面上,小物块A以某一初速度
的长木板B静止放在水平冰面上,小物块A以某一初速度 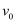 从木板B的左端滑上长木板B,直到A、B的速度达到相同,此时A、B的速度为
从木板B的左端滑上长木板B,直到A、B的速度达到相同,此时A、B的速度为  ,然后A、B又一起在水平冰面上滑行了
,然后A、B又一起在水平冰面上滑行了  后停下.若小物块A可视为质点,它与长木板B的质量相同,A、B间的动摩擦因数
后停下.若小物块A可视为质点,它与长木板B的质量相同,A、B间的动摩擦因数  ,取
,取  求:
求:
 的长木板B静止放在水平冰面上,小物块A以某一初速度
的长木板B静止放在水平冰面上,小物块A以某一初速度 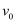 从木板B的左端滑上长木板B,直到A、B的速度达到相同,此时A、B的速度为
从木板B的左端滑上长木板B,直到A、B的速度达到相同,此时A、B的速度为  ,然后A、B又一起在水平冰面上滑行了
,然后A、B又一起在水平冰面上滑行了  后停下.若小物块A可视为质点,它与长木板B的质量相同,A、B间的动摩擦因数
后停下.若小物块A可视为质点,它与长木板B的质量相同,A、B间的动摩擦因数  ,取
,取  求:
求: 
-
(1) 木板与冰面的动摩擦因数

-
(2) 小物块A的初速度
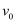
小铁块置于薄木板右端,薄木板放在光滑的水平地面上,铁块的质量大于木板的质量.t=0时使两者获得等大反向的初速度开始运动,t=t1时铁块刚好到达木板的左端并停止相对滑动,此时与开始运动时的位置相比较,下列示意图符合实际的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图甲所示,粗糙水平面上放置一块长L=2m,质量M=2kg的薄木板,一质量为m=1kg的木块放在木板的右端,轻质细线左端固定在墙上,右端通过力传感器连在木块上.现对木板施加一水平向右的力F,利用传感器连接计算机绘制出细线拉力(F)与时间(t)的关系如图乙所示.(g=10m/s2)
试分析

-
(1) 木块与木板之间的动摩擦因数
 多大:
多大:
-
(2) 已知木块与地面、木板与地面之间的动摩擦因数均为
 =0.2,现剪断细线,对木板施加向右的恒力F=11N,并开始计时,则t=4s时,木块的速度多大?
=0.2,现剪断细线,对木板施加向右的恒力F=11N,并开始计时,则t=4s时,木块的速度多大?
如图甲所示,小物块A放在长木板B的左端,一起以v0的速度在水平台阶上向右运动,已知台阶MN光滑,小物块与台阶PQ部分动摩擦因数  ,台阶的P点切线水平且与木板等高,木板撞到台阶后立即停止运动,小物块继续滑行。从木板右端距离台阶P点s=8m开始计时,得到小物块的v—t图像,如图乙所示。小物块3s末刚好到达台阶P点,4s末速度刚好变为零。若图中
,台阶的P点切线水平且与木板等高,木板撞到台阶后立即停止运动,小物块继续滑行。从木板右端距离台阶P点s=8m开始计时,得到小物块的v—t图像,如图乙所示。小物块3s末刚好到达台阶P点,4s末速度刚好变为零。若图中 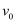 和
和 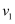 均为未知量,重力加速度g取10m/s2 , 下列说法中正确的是( )
均为未知量,重力加速度g取10m/s2 , 下列说法中正确的是( )
 ,台阶的P点切线水平且与木板等高,木板撞到台阶后立即停止运动,小物块继续滑行。从木板右端距离台阶P点s=8m开始计时,得到小物块的v—t图像,如图乙所示。小物块3s末刚好到达台阶P点,4s末速度刚好变为零。若图中
,台阶的P点切线水平且与木板等高,木板撞到台阶后立即停止运动,小物块继续滑行。从木板右端距离台阶P点s=8m开始计时,得到小物块的v—t图像,如图乙所示。小物块3s末刚好到达台阶P点,4s末速度刚好变为零。若图中 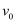 和
和 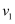 均为未知量,重力加速度g取10m/s2 , 下列说法中正确的是( )
均为未知量,重力加速度g取10m/s2 , 下列说法中正确的是( ) 
A . 由题中数据可知,木板长度为2.5m
B . 小物块在P点的速度为2m/s
C . 小物块和木板的初速度  D . 小物块与木板间动摩擦因数
D . 小物块与木板间动摩擦因数 
 D . 小物块与木板间动摩擦因数
D . 小物块与木板间动摩擦因数 
如图所示,一长木板B放在粗糙的水平地面上,在B的左端放一物体A,现以恒定的外力F拉A,经一段时间物块A从长木板B的右端拉出,且在此过程中以地面为参考系, 长木板B也向右移动一段距离。则在此过程中( )
![]()
A . 外力F对A做的功等于A和B动能的增量
B . A对B摩擦力做的功与B对A摩擦力做的功绝对值相等
C . 外力F做的功等于A,B动能的增量与系统由于摩擦而产生的热量之和
D . A对B摩擦力做的功等于B动能的增量和B与地面之间摩擦产生的热量之和
如图所示,长木板放置在水平面上,一小物块置于长木板的中央,长木板和物块的质量均为m,物块与木板间的动摩擦因数为μ,木板与水平面间动摩擦因数  ,已知最大静摩擦力与滑动摩擦力大小相等,重力加速度为g.现对物块施加一水平向右的拉力F,则木板加速度大小a可能是 ( )
,已知最大静摩擦力与滑动摩擦力大小相等,重力加速度为g.现对物块施加一水平向右的拉力F,则木板加速度大小a可能是 ( )
 ,已知最大静摩擦力与滑动摩擦力大小相等,重力加速度为g.现对物块施加一水平向右的拉力F,则木板加速度大小a可能是 ( )
,已知最大静摩擦力与滑动摩擦力大小相等,重力加速度为g.现对物块施加一水平向右的拉力F,则木板加速度大小a可能是 ( ) 
A . a=μg
B . a=  C . a=
C . a=  D . a=
D . a=  -
- 
 C . a=
C . a=  D . a=
D . a=  -
- 
如图所示,一质量为2kg。长度为1.8m的长木板A静止放置于粗糙水平地面上,木板与水平地面间的动摩擦因数为0.04。一小物块C以3m/s的速度冲上木板A左端,小物块与木板间的动摩擦因数为0.2,若小物块的质量为1kg,最大静摩擦力与滑动摩擦力大小相等,取重力加速度大小g=10m/s2。求:

-
(1) 开始运动时小物块C和木板A的加速度大小;
-
(2) 木板A的最大速度。
如图所示,水平面上的木板B和物块A(可视为质点)用一根细绳通过动滑轮连接,木板B长L=2 m,滑轮两侧细线保持水平且足够长.已知A、B间的动摩擦因数μ1=0.4,B与地面间的动摩擦因数μ2=0.1,物块A、木板B的质量分别为mA=1kg、mB=2 kg,不计细线和滑轮的质量,设最大静摩擦力等于滑动摩擦力,g取l0m/s2 . 开始时A在B的中间位置且A、B均静止,现在滑轮的轴上施加水平向右的拉力F.

-
(1) 若拉力F=F1=6N,求B对A的摩擦力.
-
(2) 拉力F至少大于多少,才能使A、B发生相对滑动?
-
(3) 若拉力F=F2=22N,求从施加拉力到A由B上滑落的过程中系统因摩擦而产生的热量.
质量为  的平板小车后端放有质量为
的平板小车后端放有质量为  的小铁块,它和车之间的动摩擦因数
的小铁块,它和车之间的动摩擦因数  。开始时,车和铁块均以
。开始时,车和铁块均以  的速度在光滑水平面上向右运动,如图所示。车到右端与墙发生正碰,设碰撞时间极短,碰撞中无机械能损失,且车身足够长,运动过程中铁块总不能和墙相碰,求:
的速度在光滑水平面上向右运动,如图所示。车到右端与墙发生正碰,设碰撞时间极短,碰撞中无机械能损失,且车身足够长,运动过程中铁块总不能和墙相碰,求:
 的平板小车后端放有质量为
的平板小车后端放有质量为  的小铁块,它和车之间的动摩擦因数
的小铁块,它和车之间的动摩擦因数  。开始时,车和铁块均以
。开始时,车和铁块均以  的速度在光滑水平面上向右运动,如图所示。车到右端与墙发生正碰,设碰撞时间极短,碰撞中无机械能损失,且车身足够长,运动过程中铁块总不能和墙相碰,求:
的速度在光滑水平面上向右运动,如图所示。车到右端与墙发生正碰,设碰撞时间极短,碰撞中无机械能损失,且车身足够长,运动过程中铁块总不能和墙相碰,求: 
-
(1) 铁块相对小车的总位移;
-
(2) 小车和墙第一次相碰后,小车所走的总路程。
如图所示,质量为M=5.0kg的长木板B静止在粗糙水平面上,长木板B右端距离平台DC左边距离为34.5m,竖直平面内半径R=0.4m的光滑半圆形轨道与平台DC右端相切于C点,平台与长木板B等高,在半圆轨道最高点固定一弹性挡板P(小物块与弹性挡板P相碰后以原速率反弹)。某时刻一质量为m=1.0kg的小木块A(可视为质点),以35m/s的初速度从左端滑上长木板,同时用一水平向右的恒力F=11N拉动长木板,使其向右做匀加速直线运动,当小木块A运动到长木板B的最右端时,二者恰好相对静止,此时撤去恒力F,随后长木板B与平台DC左端相碰,碰后长木板B速度为0,小木块A以碰前速度滑上平台,已知长木板与地面间动摩擦因数μ1=0.1,长木板与小木块间的动摩擦因数μ2=0.5,平台上铺设一种特殊材料,使得小物块A滑上平台后所受阻力大小与其速度大小成正比(即F阻=kv,k=2Ns/m),方向与速度方向相反,重力加速度g=10m/s2。求:

-
(1) 小木块A在长木板B上滑动过程中两者的加速度大小各为多少;
-
(2) 长木板B的长度L和小木块A与长木板B因摩擦产生的热量Q;
-
(3) 若小物块A能冲上半圆轨道,并能从半圆轨道上返回到平台DC上,平台DC的长度S应满足什么条件。(结果可以用根式表示)
如图所示,粗糙水平地面上有一长木板A,其长度为  ,质量为
,质量为  ,与地面间的动摩擦因数为
,与地面间的动摩擦因数为  ,在其左端有一个物块
,在其左端有一个物块  ,质量为
,质量为  ,物块
,物块  与长木板A之间的动摩擦因数为
与长木板A之间的动摩擦因数为  ,最大静摩擦力等于滑动摩擦力,重力加速度
,最大静摩擦力等于滑动摩擦力,重力加速度  ,用一水平向右的恒力作用在物块
,用一水平向右的恒力作用在物块  上。求:
上。求:
 ,质量为
,质量为  ,与地面间的动摩擦因数为
,与地面间的动摩擦因数为  ,在其左端有一个物块
,在其左端有一个物块  ,质量为
,质量为  ,物块
,物块  与长木板A之间的动摩擦因数为
与长木板A之间的动摩擦因数为  ,最大静摩擦力等于滑动摩擦力,重力加速度
,最大静摩擦力等于滑动摩擦力,重力加速度  ,用一水平向右的恒力作用在物块
,用一水平向右的恒力作用在物块  上。求:
上。求: 
-
(1) 当
 为
为  时,A、
时,A、  之间的摩擦力的大小;
之间的摩擦力的大小;
-
(2) 当
 为
为  时,物块
时,物块  运动到木板A右端所需的时间
运动到木板A右端所需的时间  。
。
如图所示,一长木板,质量M=0.4kg,静止在水平面上,长木板与水平面间的动摩擦因数μ1=0.1;一质量m=0.4kg的小滑块以v0=6m/s的速度从长木板的右端滑上长木板,滑块与长木板间动摩擦因数μ2=0.4,小滑块可视为质点。求:

-
(1) 小滑块刚滑上长木板时,长木板、小滑块的加速度大小a1、a2;
-
(2) 小滑块不从长木板滑下,长木板的最少长度L。
如图所示,长木板静止在光滑的水平面上,小铁块静止在长木板左端,长木板右端紧靠固定在水平面上的弹性挡板,某时刻小铁块自长木板左端以 的速度向右运动,经过一段时间后与挡板相碰,碰撞过程没有能量损失,最终小铁块恰好没有从长木板上滑下。已知小铁块与长木板质量均为m=1kg,二者间的动摩擦因数
的速度向右运动,经过一段时间后与挡板相碰,碰撞过程没有能量损失,最终小铁块恰好没有从长木板上滑下。已知小铁块与长木板质量均为m=1kg,二者间的动摩擦因数 , 重力加速度
, 重力加速度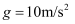 。求:
。求:
 的速度向右运动,经过一段时间后与挡板相碰,碰撞过程没有能量损失,最终小铁块恰好没有从长木板上滑下。已知小铁块与长木板质量均为m=1kg,二者间的动摩擦因数
的速度向右运动,经过一段时间后与挡板相碰,碰撞过程没有能量损失,最终小铁块恰好没有从长木板上滑下。已知小铁块与长木板质量均为m=1kg,二者间的动摩擦因数 , 重力加速度
, 重力加速度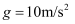 。求:
。求:
-
(1) 小铁块和长木板的最终速度及长木板的长度;
-
(2) 整个过程中小铁块和长木板因摩擦产生的热量。
如图所示,质量M=8kg的长木板B沿水平地面向左运动,同时受到水平向右的恒力F=48N的作用,当长木板B的速度v=6m/s时,从长木板B的左端滑上一质量m=2kg的小木块A,此时小木块A的速度大小也为v=6m/s,已知小木块A未从长木板B的右端滑下,小木块A与长木板B和长木板B与地面之间的动摩擦因数均为μ=0.2,重力加速度g=10m/s2。求:

-
(1) 长木板B向左运动的最大位移;
-
(2) 求A、B速度相等时,A离长木板B左端的距离为多少。
-
(3) 判断A、B速度相等时,A、B是否会发生相对滑动?
最近更新
- 善 ①以咨诹善道,察纳雅言(《出
- When women sit together to watch a movie on TV, they
- 如图表示细胞发生的一系列变化过程,有关分
- 某化学反应的反应物和产物如下: KMnO4 + KI
- 若夫日出而林霏开,云归而岩穴暝,晦明变化
- 在△中,,,,则△是_________.
- 下列说法正确的是
- 下列有关实验原理或实验操作正确的是A.在
- 呼吸的全过程包括下面四个环节 , 其正确顺序
- 下列实验现象描述正确的是( ) A.打开盛有浓
- —How I wish everyone were kind and respected their elders
- 如图所示,质量均为m的两木块A与B叠放在水平
- 下列各句没有语病的一项是( ) A.如何
- 下列各选项你认为不属于环境问题的是 A.撒哈
- here was a ____________(惊恐的) look on his face hearing
- 在研究物质结构时,使用了“原子”的概念;
- 某红色固体粉末样品可能含有Fe2O3和Cu2O中的一
- 下列材料制成的容器既不能用来盛放盐酸,也
- Ⅰ.用下列序号填空: ①烧杯 ②试管
- Why should mankind explore space? Why should money, time a



