九年级(初三)数学下学期下册试题
在△ABC中,∠C=90°,tanA= 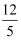 ,△ABC的周长为60,那么△ABC的面积为( )
,△ABC的周长为60,那么△ABC的面积为( )
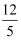 ,△ABC的周长为60,那么△ABC的面积为( )
,△ABC的周长为60,那么△ABC的面积为( )
A . 60
B . 30
C . 240
D . 120
如图,在△ABC和△ADE中,  ,点B,D,E在一条直线上.求证:△ABD∽△ACE.
,点B,D,E在一条直线上.求证:△ABD∽△ACE.
 ,点B,D,E在一条直线上.求证:△ABD∽△ACE.
,点B,D,E在一条直线上.求证:△ABD∽△ACE.
比较大小: 
 .(填“
.(填“  ,
, 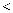 或
或  ”)
”)

 .(填“
.(填“  ,
, 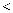 或
或  ”)
”)
如图,  与
与  位似,点O是它们的位似中心,其中
位似,点O是它们的位似中心,其中 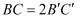 ,若点A的坐标为
,若点A的坐标为 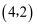 ,则
,则 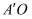 的长度为( )
的长度为( )
 与
与  位似,点O是它们的位似中心,其中
位似,点O是它们的位似中心,其中 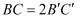 ,若点A的坐标为
,若点A的坐标为 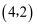 ,则
,则 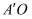 的长度为( )
的长度为( ) 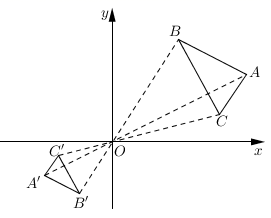
A . 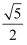 B .
B .  C .
C . 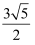 D .
D . 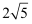
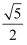 B .
B .  C .
C . 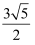 D .
D . 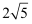
一次函数y=ax+b与反比例函数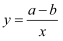 , 其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )
, 其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )
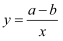 , 其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )
, 其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )
A . 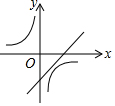 B .
B . 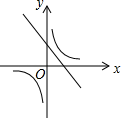 C .
C . 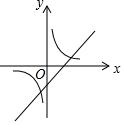 D .
D . 
 B .
B . 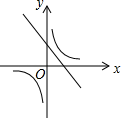 C .
C .  D .
D . 
在平面直角坐标系xOy中,抛物线y=mx2﹣4mx(m≠0)与x轴交于A,B两点(点A在点B的左侧).
-
(1) 求点A,B的坐标及抛物线的对称轴;
-
(2) 过点B的直线l与y轴交于点C,且tan∠ACB=2,直接写出直线l的表达式;
-
(3) 如果点P(x1 , n)和点Q(x2 , n)在函数y=mx2﹣4mx(m≠0)的图象上,PQ=2a且x1>x2 , 求x12+ax2﹣6a+2的值.
在反比例函数 的图象的每一条曲线上,y随x的增大而增大,则k的值可以是( )
的图象的每一条曲线上,y随x的增大而增大,则k的值可以是( )
 的图象的每一条曲线上,y随x的增大而增大,则k的值可以是( )
的图象的每一条曲线上,y随x的增大而增大,则k的值可以是( )
A . -1
B . 0
C . 1
D . 2
计算:  .
.
 .
.
如图,一艘渔船正以30海里/小时的速度由西向东赶鱼群,在A处看风小岛C在船的北偏东60°.40分钟后,渔船行至B处,此时看见小岛C在船的北偏东30°.已知以小岛C为中心周围10海里以内为我军导弹部队军事演习的着弹危险区,问这艘渔船继续向东追赶鱼群,是否有进入危险区的可能.

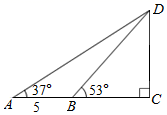
如图,小明家附近有一观光塔CD,他发现当光线角度变化时,观光塔的影子在地面上的长度也发生变化.经测量发现,当小明站在点A处时,塔顶D的仰角为37°,他往前再走5米到达点B(点A,B,C在同一直线上),塔顶D的仰角为53°,则观光塔CD的高度约为 .(精确到0.1米,参考数值:tan37°≈  ,tan53°≈
,tan53°≈  )
)
 ,tan53°≈
,tan53°≈  )
) 
如图,长方形广告牌架在楼房顶部,已知CD=2m,经测量得到∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.(参考数据:tan37°≈0.75,  ≈1.732,结果精确到0.1m)
≈1.732,结果精确到0.1m)
 ≈1.732,结果精确到0.1m)
≈1.732,结果精确到0.1m) 
用12个大小相同的小正方体搭成的几何体如图所示
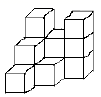
-
(1) 画出该几何体的从三个方向看的形状图
-
(2) 若小正方体的棱长为1,求出该几何体的表面积.
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5  ,则∠B的度数是( )
,则∠B的度数是( )
 ,则∠B的度数是( )
,则∠B的度数是( )
A . 30°
B . 45°
C . 50°
D . 60°
已知反比例函数经过点(﹣3,3),求这个函数表达式.
如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.

-
(1) 求该二次函数的解析式及点M的坐标;
-
(2) 若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;
-
(3) 点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).
如图1,这是一款升降电脑桌,它的升降范围在0~40cm,图2是它的示意图.已知EF∥MN,点A,B在MN上滑动,点D,C在EF上滑动,AC,BD相交于点O,OA=OB=OC=OD=30cm.


-
(1) 如图2,当∠OAB=30°时,求这款电脑桌当前的高度.
-
(2) 当电脑桌从图2位置升到最大高度(如图3)时,求∠OAB的大小及点A滑动的
距离.
(结果精确到0.1;参考数据:
 ≈1.73,sin42.1°≈0.67,cos42.1°≈0.74,sin47.9°≈0.74,cos47.9°≈0.67)
≈1.73,sin42.1°≈0.67,cos42.1°≈0.74,sin47.9°≈0.74,cos47.9°≈0.67)
已知:α为锐角,关于x的一元二次方程3x2﹣2  x+tanα=0有两个相等的实数根.
x+tanα=0有两个相等的实数根.
 x+tanα=0有两个相等的实数根.
x+tanα=0有两个相等的实数根.-
(1) 求锐角α;
-
(2) 求方程的根.
在Rt△ABC中,∠C=90°,若sinA=  ,则cosB的值等于( )
,则cosB的值等于( )
 ,则cosB的值等于( )
,则cosB的值等于( )
A .  B .
B . 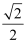 C .
C .  D . 1
D . 1
 B .
B . 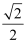 C .
C .  D . 1
D . 1
对于双曲线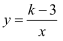 , 当
, 当 时,
时, 随
随 的增大而增大,则
的增大而增大,则 的取值范围是.
的取值范围是.
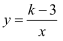 , 当
, 当 时,
时, 随
随 的增大而增大,则
的增大而增大,则 的取值范围是.
的取值范围是.
如图,矩形ABCD中,AB=4,AD=5,E为BC上一点,BE∶CE=3∶2,连接AE,点P从点A出发,沿射线AB的方向以每秒1个单位长度的速度匀速运动,过点P作PF∥BC交直线AE于点F.

-
(1) 线段AE=;
-
(2) 设点P的运动时间为t(s),EF的长度为y,求y关于t的函数关系式,并写出t的取值范围;
-
(3) 当t为何值时,以F为圆心的⊙F恰好与直线AB、BC都相切?并求此时⊙F的半径.
最近更新
- You are still angry_________ me , aren’t you? A. on
- 下图为人的关节模式图,请根据图回答相关问题。(1)图中③称为________,④称为________。 (2)图中⑤是_
- 2009年4月14日的中国民族报报道,国务院新闻办公室4月13日发表我国首份《国家人权行动计划(2009~2010年)》
- 第二节 书面表达(共计25分) 假设你应邀参加学校组织的“英语学习师生座谈会”,请你根据下表所提示的信息,用英语写一篇发
- 若正比例函数y=kx图像经过点(1,2),则K A.-0.5 B.-2 C. 0.5 D.2
- 下列有机物的命名正确的是( ) A.:CH3C(CH3)3 :异戊烷 B.:对二甲苯 C.:2,4,4-三甲基己烷
- 不等式≥3的解集在数轴上(如图)表示正确的是 ( ).
- 下列关于细胞结构和功能的叙述不正确的是() A.膜的组成和结构的相似性是细胞内生物膜相互转化的基础 B.效应B细胞中高尔
- 以下符号所表示的微粒:①N;②NO;③CO2;④NH4+;⑤N2;⑥Ne;⑦Na;⑧H2O;⑨O2﹣;⑩Na+. (1)
- 根据课文默写古诗文。(10分) (1)______________________,悠然见南山。山气日夕佳,飞鸟相与还。
- 图表明了青菜价格的变化,下列各项能正确揭示其内涵的是 ( )A.工作日和双休日的变化是影响青菜价格的根本因素 B.
- 小林发现妈妈在面粉和好后,不间断地撒上一些用拉面剂和水(按1:3比例)调制出来的溶液并不断揉搓,做出来的拉面面条筋道,色
- 已知奇函数f(x)=-(1)求实数m的值,并在给出图的直角坐标系中画出y=f(x)的图像;(2)若函数f(x)在区间[-
- 如图,质点在半径为2的圆周上逆时针运动,其初始位置为(,),角速度为1,那么点到轴距离关于时间的函数图像大致为
- --What is the cost of you shirts here, sir? --It depends on
- In China,chain restaurants – especially the big multinationa
- 冰霜正惨凄,____________________________。(刘祯《赠从弟》)
- 下列做法中,为了减小压强的是 A.菜刀的刀口做得很薄 B.铁路
- 一个正方体有 个面.
- 基因的自由组合定律揭示的是 A.非等位基因之间的关系 B.非同源染色体上非等位基因之间的关系 C.同源染色体上不同位置基



