九年级(初三)数学下学期下册试题
如图,在平面直角坐标系中,第二象限内的点P是反比例函数y=  (k≠0)图象上的一点,过点P作PA⊥x轴于点A , 点B为AO的中点若△PAB的面积为3,则k的值为( )
(k≠0)图象上的一点,过点P作PA⊥x轴于点A , 点B为AO的中点若△PAB的面积为3,则k的值为( )
 (k≠0)图象上的一点,过点P作PA⊥x轴于点A , 点B为AO的中点若△PAB的面积为3,则k的值为( )
(k≠0)图象上的一点,过点P作PA⊥x轴于点A , 点B为AO的中点若△PAB的面积为3,则k的值为( ) 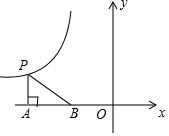
A . 6
B . ﹣6
C . 12
D . ﹣12
如图,在每个小正方形的边长为1的网格中,  的顶点B , C均落在格点上,点A在网格线上,且
的顶点B , C均落在格点上,点A在网格线上,且 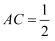 .
.
 的顶点B , C均落在格点上,点A在网格线上,且
的顶点B , C均落在格点上,点A在网格线上,且 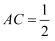 .
. 
-
(1) 线段
 的长等于;
的长等于;
-
(2) 以
 为直径作半圆,请在半圆上找一点P , 使得
为直径作半圆,请在半圆上找一点P , 使得 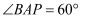 ,请用无刻度的直尺,在如图所示的网格中画出点P , 并简要说明点P的位置是如何找到的.(不要求证明)
,请用无刻度的直尺,在如图所示的网格中画出点P , 并简要说明点P的位置是如何找到的.(不要求证明)
已知圆锥的侧面积为10πcm2 , 侧面展开图的圆心角为36°,则该圆锥的母线长为( )
A . 100cm
B . 10cm
C . 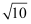 cm
D .
cm
D . 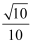 cm
cm
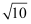 cm
D .
cm
D . 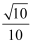 cm
cm
sin30°的值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图、两条宽度为1的纸条,交叉重叠在一起,且它们的较小交角为α,则它们重叠部分(阴影部分)的面积为 ( )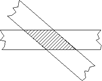
A .  B .
B .  C . sinα
D . 1
C . sinα
D . 1
 B .
B .  C . sinα
D . 1
C . sinα
D . 1
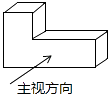
如图是由7个相同的小立方块搭成的几何体.已知它的左视图如下.请画出它的主视图和俯视图.

如图,△ABC中,∠ACB=90°,sinA=  ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
 ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.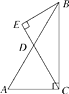
-
(1) 求线段CD的长;
-
(2) 求cos∠ABE的值。
已知反比例函数 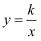 ,在每一个象限内y随x的增大而增大,点A在这个反比例函数图象上,AB⊥x轴,垂足为点B,△ABO的面积为9,那么反比例函数的解析式为( )
,在每一个象限内y随x的增大而增大,点A在这个反比例函数图象上,AB⊥x轴,垂足为点B,△ABO的面积为9,那么反比例函数的解析式为( )
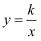 ,在每一个象限内y随x的增大而增大,点A在这个反比例函数图象上,AB⊥x轴,垂足为点B,△ABO的面积为9,那么反比例函数的解析式为( )
,在每一个象限内y随x的增大而增大,点A在这个反比例函数图象上,AB⊥x轴,垂足为点B,△ABO的面积为9,那么反比例函数的解析式为( )
A . 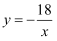 B .
B . 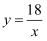 C .
C . 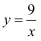 D .
D . 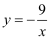
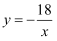 B .
B . 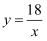 C .
C . 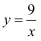 D .
D . 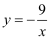
某山坡坡面的坡度为1:  ,则坡角是 度.
,则坡角是 度.
 ,则坡角是 度.
,则坡角是 度.
如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙O的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.

-
(1) 求证:AD平分∠BAC;
-
(2) 若AC=8,tan∠DAC=
 ,求⊙O的半径.
,求⊙O的半径.
如图,身高为1.8米的某学生想测量学校旗杆的高度,当他站在B处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AB=2米,BC=18米,则旗杆CD的高度是米.
某厂为满足市场需求,改造了10条口罩生产线,每条生产线每天可生产口罩500个,如果每增加一条生产线,每条生产线每天就会少生产20个口罩,设增加x条生产线(x为正整数),每条生产线每天可生产口罩y个.
-
(1) 请直接写出y与x之间的函数表达式是;
-
(2) 设该厂每天可以生产的口罩w个,请求出w与x的函数关系式,并求出当x为多少时,每天生产的口罩数量w最多?最多为多少个?
-
(3) 由于口罩供不应求,所以每天生产的口罩数量不能低于6000个,请直接写出需要增加的生产线x条的取值范围.
一个正方体的侧面展开图如图所示,用它围成的正方体只可能是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知正方体的一个平面展开图如图所示,则在原正方体上“百”的对面是.
如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?
(结果精确到0.1cm,参考数据:  ≈1.732)
≈1.732)
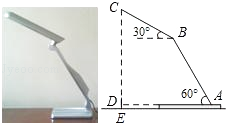
如图所示的支架是由两个长方体构成的组合体,则它的主视图是( )
A .  B .
B .  C .
C .  D .
D . 
如图,在  中,
中,  ,
,  ,
,  ,则
,则  的面积是( )
的面积是( )
 中,
中,  ,
,  ,
,  ,则
,则  的面积是( )
的面积是( ) 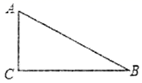
A .  B .
B .  C .
C . 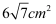 D .
D . 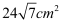
 B .
B .  C .
C . 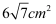 D .
D . 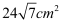
一个反比例函数的图象位于第二、四象限.请你写出一个符合条件的解析式是 .
如图,已知⊙O为△ABC的外接圆,BC为⊙O的直径,作射线BF,使得BA平分∠CBF,过点A作AD⊥BF于点D。

-
(1) 求证:DA为⊙O的切线;
-
(2) 若BD=1,tan∠ABD=2,求⊙O的半径。
如图,二次函数  的图象与x轴交于点A、B,已知
的图象与x轴交于点A、B,已知  与y轴交于点
与y轴交于点  ,该抛物线的顶点为点D.
,该抛物线的顶点为点D.
 的图象与x轴交于点A、B,已知
的图象与x轴交于点A、B,已知  与y轴交于点
与y轴交于点  ,该抛物线的顶点为点D.
,该抛物线的顶点为点D. 
-
(1) 二次函数的表达式为,点D的坐标为;
-
(2) 连接BC.
①在抛物线上存在一点P,使得
 ,求点P的坐标;
,求点P的坐标;②若
 是抛物线上动点,则是否存在点
是抛物线上动点,则是否存在点  ,使得
,使得  ?若存在,直接写出点
?若存在,直接写出点  的横坐标的取值范围;若不存在,说明理由.
的横坐标的取值范围;若不存在,说明理由.
最近更新
- 请以“有一种力量叫 ”为题,写一篇文章。 要求:①先将题目补充完整,题目横线处可以填写:“感动”“母爱
- 我们的生活离不开能源,而能源的开发和利用离不开化学。现代社会不仅对能源的需求量越来越大,要求也越来越高,我们已经进入第三
- 把直角坐标系的原点作为极点,x轴的正半轴作为极轴,并且在两种坐标系中取相同的长度单位.若曲线的极坐标方程是ρ2=,则它的
- 实践表明,我国的民主选举将在相当长的一段时间内采用直接选举和间接选举相结合的方式。选择不同选举方式的主要制约因素有(
- Ⅰ.将刮去氧化膜的镁片投入沸水中,反应的化学方程式为 。Ⅱ.若用灼热的镁粉与水蒸气反应,则在生成H2的同时还可能得到
- 粗盐水过滤后仍含有可溶性的、、等杂质,通过如下几个实验步骤可以除去这些杂质。加入稍过量的溶液;加入稍过量的溶液;加入稍过
- 阅读材料,回答下列问题。 材料一 在2008奥运圣火传递中,一些西方国家扮演极不光彩的角色。针对这种情况,博客
- ---where’s my handbag? I can’t find it. --- You must ha
- 选出下列加点字注音完全正确的一项。( ) A.犷野(guǎng) 蓦然(mù) 尽态极妍(
- 阅读理解:对于任意正实数a、b,∵≥0, ∴≥0, ∴≥,只有当a=b时,等号成立. 结论:在≥(a、b均为正实数)中,
- 下列各组性质比较中正确的是 ( ) A.酸性:HF>HCl>HBr>
- 洞里萨湖是东南亚最大的淡水湖,通过洞里萨河与湄公河相连。根据材料和图3,回答3-4题。3.图中显示洞里萨湖的面积约为(
- 中国始终不渝地走和平发展道路,是中国政府和人民根据时代发展潮流和自身根本利益作出的战略抉择。中国走和平发展道路需要(
- 关于反应的说法错误的是( )A.外界条件可以改变平衡状态 B.达到平衡时正、逆反应
- 某药品说明书中标明:本品每100 mL含碘5mg、镁65 mg、铜2 mg、铁1.5 mg、锰1mg,这里所标的各成分是
- 将m g含氧化铁、氧化铜或氧化亚铁的样品投入物质的量浓度为1 mol/L的2 L盐酸中恰好完全反应。若向等质量的该样品中
- 伊斯兰教、基督教、犹太教把下面哪个城市看作圣城:( ) A、巴格达 B、新德里
- 八年级数学课上,朱老师出示了如下框中的题目.小聪与同桌小明讨论后,进行了如下解答: (1)特殊情况·探索结论 当点E为A
- 下列离子方程式书写正确的是A.过量的SO2通入NaOH溶液中:SO2+2OH-+H2OB.Fe(NO3)3溶液中加入过量
- 社会主义市场经济是和社会主义基本制度结合在一起的。社会主义市场经济的根本目标是 () A、建立健全社会诚信体系



