九年级(初三)数学下学期下册试题
如果反比例函数的图象经过点P(﹣3,﹣1),那么这个反比例函数的表达式为( )
A . y= B . y=﹣
B . y=﹣ C . y=
C . y= x
D . y=﹣
x
D . y=﹣ x
x
 B . y=﹣
B . y=﹣ C . y=
C . y= x
D . y=﹣
x
D . y=﹣ x
x
为加快城乡对接,建设全域美丽乡村,某地区对A,B两地间的公路进行改建.如图,A,B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,  . (结果精确到
. (结果精确到  千米,参考数据:
千米,参考数据:  )
)
 . (结果精确到
. (结果精确到  千米,参考数据:
千米,参考数据:  )
) 
-
(1) 开通隧道前,汽车从A地到B地大约要走多少千米?
-
(2) 开通隧道后,汽车从A地到B地大约可以少走多少千米?
如图,在正方形  中,点E在
中,点E在  边上,
边上,  于点G,交
于点G,交  于点F.若
于点F.若  ,
,  ,则
,则  的面积与四边形
的面积与四边形  的面积之比是( )
的面积之比是( )
 中,点E在
中,点E在  边上,
边上,  于点G,交
于点G,交  于点F.若
于点F.若  ,
,  ,则
,则  的面积与四边形
的面积与四边形  的面积之比是( )
的面积之比是( ) 
A .  B .
B .  C .
C .  D .
D . 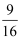
 B .
B .  C .
C .  D .
D . 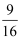
在Rt△ABC中,∠C=90°,sinA=  ,则∠A的度数是( )
,则∠A的度数是( )
 ,则∠A的度数是( )
,则∠A的度数是( )
A . 30°
B . 45°
C . 60°
D . 90°
已知y=(k2+k) 中,请问:k为何值,y是x的反比例函数.
中,请问:k为何值,y是x的反比例函数.
 中,请问:k为何值,y是x的反比例函数.
中,请问:k为何值,y是x的反比例函数.
如图,在△ABC中,DE∥AB,且 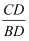 =
=  ,则
,则  的值为( )
的值为( )
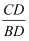 =
=  ,则
,则  的值为( )
的值为( ) 
A .  B .
B . 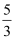 C .
C .  D .
D . 
 B .
B . 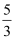 C .
C .  D .
D . 
如图,△ABC中,DF∥EG∥BC,且AD=DE=EB,则△ABC被分成的三部分的面积比SⅠ∶SⅡ∶SⅢ为( )

A . 1∶1∶1
B . 1∶3∶5
C . 1∶2∶3
D . 1∶4∶9
如图所示,某校数学兴趣小组利用标杆BE测量物的高度,已知标杆BE高1.5m,测得AB=1.2m,AC=14m,则建筑物CD的高是( )

A . 17.5m
B . 17m
C . 16.5m
D . 18m
如图,小明、小华分别位于一条笔直公路PQ上的两点A , B处,点C处为一超市.测得  ,
,  ,A , B之间距离为3.8km,求小明、小华分别距离超市多少千米(结果保留小数点后一位).
,A , B之间距离为3.8km,求小明、小华分别距离超市多少千米(结果保留小数点后一位).
 ,
,  ,A , B之间距离为3.8km,求小明、小华分别距离超市多少千米(结果保留小数点后一位).
,A , B之间距离为3.8km,求小明、小华分别距离超市多少千米(结果保留小数点后一位). 参考数据:  ,
,  ,
,  ,
,  ,
,  ,
,  .
.

如图,AD是△ABC的中线,tanB= , cosC=
, cosC= , AC=
, AC= . 求:
. 求:
 , cosC=
, cosC= , AC=
, AC= . 求:
. 求:(1)BC的长;
(2)sin∠ADC的值.

若△ABC∽△DEF,相似比为2:3,则S△ABC:S△DEF=.
在矩形ABCD中,AB=9cm,E是直线CD上一点,连接AC,BE,若AC与BE交于点F且DE=3cm,则EF:BE的值是.
计算:|﹣3|+  •tan30°﹣(3.14﹣π)0
•tan30°﹣(3.14﹣π)0
 •tan30°﹣(3.14﹣π)0
•tan30°﹣(3.14﹣π)0
-
(1) 计算:
 .
.
-
(2) 已知线段
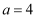 ,
,  ,求线段
,求线段  ,
,  的比例中项.
的比例中项.
计算:  .
.
 .
.
如图,已知双曲线y=  (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为( )
(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为( )
 (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为( )
(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为( )
A . 12
B . 9
C . 6
D . 4
下图是由8个大小相同的小正方体搭成的几何体,则这个几何体的主视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于点B成中心对称的图形△A1BC1;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2 , 并直接写出C2点坐标.
如图, 中,
中, 于点D.
于点D.
 中,
中, 于点D.
于点D.
-
(1) 求证:
 ;
;
-
(2) 如果
 , 求
, 求 的长.
的长.
已知反比例函数y=  的图象位于第一、第三象限,则k的取值范围是( )
的图象位于第一、第三象限,则k的取值范围是( )
 的图象位于第一、第三象限,则k的取值范围是( )
的图象位于第一、第三象限,则k的取值范围是( )
A . k>8
B . k≥8
C . k≤8
D . k<8
最近更新
- 2008年6月6日上午,第十六届中国昆明进出口商品交易会在昆明国际会展中心开幕。此次昆交会有商务部首次参与主办,是历届昆
- 在丰田因质量问题而引发的“召回事件”中,中国消费者应该受到特殊青睐。因为丰田需要中国这个当前规模大、潜力大、增幅最大的区
- 位于短周期的四种主族元素A、B、C、D原子序数依次增大,已知A、C位于同一主族,A在周期表中原子半径最小。B、D的最外层
- 湖南省人民政府行政效能投诉中心“12342”投诉热线电话开通后,如果遇到省直行政机关及其工作人员有行政不作为、慢作为、乱
- 若点A(a+1,b﹣2)在第二象限,则点B(﹣a,1﹣b)在() A.第一象限B.第二象限C.第三象限D.第四象限
- 一定温度下,可逆反应A2(g)+3B2(g) 2AB3(g)达到平衡的标志是() A.容器内每减少1mol A2,同时生
- 下列物质中,不属于电解质的是( )。A.Cu B.NaCl C.NH3 D.H2SO4
- 下列说法不正确的一项是( ) A 古人一般把南面视为至尊。所以《鸿门宴》中项王、项伯东向坐;亚父南向坐,____亚父
- 没有成形细胞核的生物和没有细胞结构的生物分别是 A.乳酸杆菌和蓝藻 B.肺炎双球菌与噬
- 下列叙述正确的是()A.两种元素构成的共价化合物分子中的化学键都是极性键B.含有非极性键的化合物不一定是共价化合物
- 下列图像能正确反映对应的实验操作的是A.在加热条件下一氧化碳与一定量氧化铜反应B.在一定量的硫酸铜溶液中插入铁丝 C.t
- 某高等植物体细胞内假设有6条染色体,它们是AaBbDd,那么,一个花粉管中的两个精子中的染色体可能是() A.ABD和a
- 某同学打算用金属与稀硫酸反应制备氢气.(已知:Zn+H2SO4===ZnSO4+H2↑ Fe+H2SO4===FeSO4
- 最近我们从电视上多次看到南方某地大象三五成群进村伤人、损坏农田,农民既害怕又伤心。那么,我们对伤人的大象采取的态度是
- p{font-size:10.5pt;line-height:150%;margin:0;padding:0;}td{f
- 蜀先主庙 刘禹锡 天下英雄气,千秋尚凛然。势分三足鼎,业复五铢钱①。 得相能开国,生儿不象贤。凄凉蜀
- 如图7-5所示,长l=1.25 m、质量M=8 kg的平板车静止在光滑水平面上,车的左端放一质量m=2 kg的木块,它与
- 某市大力发展养殖业,用鸡粪生产生物有机肥并发电,用鸡毛、鸡肠等制成高蛋白的鱼饲料。鸡粪、鸡毛、鸡肠等“垃圾”不但没有污染
- 假定英语课上老师要求同桌之间交换修改作文,请你修改你同桌写的以下作文。文中共有10处语言错误,每句中最多有两处,
- 下列词语中读音全都正确的一组是 ( ) A.恬(tián)不知耻 拈(niān)轻怕重 前倨(jù)后恭



