九年级(初三)数学下学期下册试题
已知α是锐角,若sinα=
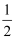 ,则α的度数是( )
,则α的度数是( )
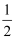 ,则α的度数是( )
,则α的度数是( )
A . 30°
B . 45°
C . 60°
D . 75°
如图,直线  ,若
,若  ,
,  ,
,  ,则线段
,则线段  的长为( )
的长为( )
 ,若
,若  ,
,  ,
,  ,则线段
,则线段  的长为( )
的长为( ) 
A . 5
B . 6
C . 7
D . 8
如图  中,AB=9,点D在边AB上,AD=5,∠B=∠ACD,则AC=
中,AB=9,点D在边AB上,AD=5,∠B=∠ACD,则AC=
 中,AB=9,点D在边AB上,AD=5,∠B=∠ACD,则AC=
中,AB=9,点D在边AB上,AD=5,∠B=∠ACD,则AC= 
如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=10,tan∠B=  ,则BC的长为( )
,则BC的长为( )
 ,则BC的长为( )
,则BC的长为( ) 
A . 6
B . 8
C . 12
D . 16
先化简,再求值:(  ﹣
﹣  )÷
)÷  ,其中x=2sin30°+
,其中x=2sin30°+  tan30°.
tan30°.
 ﹣
﹣  )÷
)÷  ,其中x=2sin30°+
,其中x=2sin30°+  tan30°.
tan30°.
在Rt△ABC中,∠C=90°,若sinA=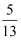 , 则cosA的值为( )
, 则cosA的值为( )
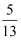 , 则cosA的值为( )
, 则cosA的值为( )
A . 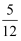 B .
B .  C .
C .  D .
D . 
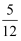 B .
B .  C .
C .  D .
D . 
数学兴趣小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点共线,请根据以上数据计算GH的长( 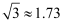 ,要求结果精确得到0.1m)
,要求结果精确得到0.1m)

某新农村乐园设置了一个秋千场所,如图所,秋千拉绳OB的长为3m,静止时,踏板到地面距离BD的长为0.6m(踏板厚度忽略不计).为安全起见,乐园管理处规定:儿童的“安全高度”为hm,成人的“安全高度”为2m(计算结果精确到0.1m)

-
(1) 当摆绳OA与OB成45°夹角时,恰为儿童的安全高度,则h= m
-
(2) 某成人在玩秋千时,摆绳OC与OB的最大夹角为55°,问此人是否安全?(参考数据:
 ≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
如图,电线杆 的高度为h,两根拉线
的高度为h,两根拉线 与
与 相互垂直,
相互垂直, , 则拉线
, 则拉线 的长度为(A、D、B在同一条直线上)( )
的长度为(A、D、B在同一条直线上)( )
 的高度为h,两根拉线
的高度为h,两根拉线 与
与 相互垂直,
相互垂直, , 则拉线
, 则拉线 的长度为(A、D、B在同一条直线上)( )
的长度为(A、D、B在同一条直线上)( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,点O是△ABC的重心,过点O作DE∥AB,分别交AC、BC于点D、E,如果  ,那么
,那么  =(结果用
=(结果用  表示).
表示).
 ,那么
,那么  =(结果用
=(结果用  表示).
表示). 
如图,平面直角坐标系中,点  ,
,  在
在  轴上,点
轴上,点  在
在  轴上,直线
轴上,直线  交双曲线
交双曲线 
 第一象限于点
第一象限于点  ,连接
,连接  ,
,  ,
,  ,若
,若  ,
,  ,
,  ,则
,则  的值是.
的值是.
 ,
,  在
在  轴上,点
轴上,点  在
在  轴上,直线
轴上,直线  交双曲线
交双曲线 
 第一象限于点
第一象限于点  ,连接
,连接  ,
,  ,
,  ,若
,若  ,
,  ,
,  ,则
,则  的值是.
的值是.

在一次数学活动课上,王老师给学生发了一张长30cm,宽20cm的长方形纸片(如图),要求折成一个高为5cm的无盖的且容积最大的长方体盒子,则该盒子的容积是

如图,以O为位似中心,在网格内作出四边形ABCD的位似图形,使新图形与原图形的相似比为2:1,并以O为原点,写出新图形各点的坐标.

在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,可以增加视觉美感.如图,按此比例设计一座高度为2m 的雷锋雕像,那么该雕像的下部设计高度约是( )(结果精确到  .参考数据:
.参考数据:  ,
,  ,
,  )
)
 .参考数据:
.参考数据:  ,
,  ,
,  )
)

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图所示的四个平面图形中,不是正方体的展开图的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .
如图,在锐角 中,
中, , AE是中线,BF和CD是高则下列结论中,正确的是(填序号).
, AE是中线,BF和CD是高则下列结论中,正确的是(填序号).
 中,
中, , AE是中线,BF和CD是高则下列结论中,正确的是(填序号).
, AE是中线,BF和CD是高则下列结论中,正确的是(填序号).
①
②
③ 是等边三角形
是等边三角形
④ .
.
如图标记了△ABC与△DEF边、角的一些数据,如果再添加一个条件使△ABC∽△DEF,那么这个条件可以是.(只填一个即可)

如图是由一些棱长都为1cm的小正方体组合成的简单几何体.

-
(1) 画该几何体的主视图、左视图和俯视图;

-
(2) 如果在这个几何体上再添加一些小正方体,并保持俯视图和左视图不变,最多可以再添加块小正方体.
已知反比例函数y=  与直线l交于点A(2,2)和点B(-1,m)
与直线l交于点A(2,2)和点B(-1,m)
 与直线l交于点A(2,2)和点B(-1,m)
与直线l交于点A(2,2)和点B(-1,m) 
-
(1) 求k与m的值;
-
(2) 求△OAB的面积.
计算:  .
.
 .
.
最近更新
- 造成藏羚羊濒临灭绝的主要原因是( )A.人类的肆虐捕杀 B.草场的退化C.森林覆盖率的下降
- _____ you will succeed inpersuading someone depends on ____
- 综合性学习。(6分) 在我国古代历史长河中,曾经出现过无数风流人物。在语文教材中,出现过的就有不少,如:孔子、孟子、诸葛
- 下列各式计算正确的是() A.3x-2x=1 B.a2+a2=a4 C.a5÷a5=a D.a3•a2=a5
- 有一排7只发光二级管,每只二级管点亮时可发出红光或绿光,若每次恰有3只二级管点亮,但相邻的两只二级管不能同时点亮,根据这
- 文学类文本阅读(18分) 大义生死 安巧林 中华民族世世代代活在那些杰出的生里,亦活在那些杰出的死里,五千年积淀的,绝
- 某科技馆中有一个展品,该展品放在较暗处,有一个不断均匀滴水的水龙头(刚滴出的水滴速度为零)在平行光源的照射下,可以观察到
- 曲线(θ为参数)的准线方程是___________.
- 分析下列各组微粒结构示意图,与表示的意义一致的是()A. 都属于金属元素 B. 都属于阳离子 C. 属
- 2010年6月5日是第38个世界环境日,世界环境日中国的主题为“低碳减排,绿色生活”. (1)由于(填化学式)气体的大量
- 有一函数y=,编写程序,输入一个x的值,输出相应y的值.
- 张明同学为了探究绿色植物的呼吸作用和光合作用,设计了如图所示装置.广口瓶内盛有少量澄清石灰水,内放一株绿色植物,瓶塞塞住
- 下列各数中,不相等的组数有( ) ①(-3)2与-32 ②(-3)2与32 ③(-2)3与-23 ④3与
- 两木块A、B由同种材料制成,,并随木板一起以相同速度向右做匀速直线运动,如图所示,设木板足够长,当木板突然停止运动后,则
- 世界上无国家分布的大洲是A.亚洲 B.拉丁美洲 C.大洋洲
- – Jack? -- ____. A. Present, Sir. B. I am, Sir C. He
- 依次填入下列各句横线处的词语,恰当的一组是() (1)这场争夺无名高地的激战整整__了八个小时。 (2)封建王朝的统治者
- 的相反数是( ) A.2 B.-2 C.
- “地球上最美的花朵不断地转化为丰硕的果实”是指 A.意识能够直接作用于客观事物 B.人们在意识的指导下创造物质财富 C.
- 函数f(x)=sinx•ln(x2+1)的部分图象可能是( ) A. B. C. D.



