九年级(初三)数学下学期下册试题
如图,直线 与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为.
与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为.
 与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为.
与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为.
反比例函数y= 与y=
与y= 在第一象限的图象如图所示,作一条平行于x轴的直线分别交双曲线于A、B两点,连接OA、OB,则△AOB的面积为( )
在第一象限的图象如图所示,作一条平行于x轴的直线分别交双曲线于A、B两点,连接OA、OB,则△AOB的面积为( )

A .  B . 2
C . 3
D . 1
B . 2
C . 3
D . 1
 B . 2
C . 3
D . 1
B . 2
C . 3
D . 1
如图是一个几何体的三视图,则该几何体的体积为.

如图,  为
为 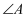 一边上的任意一点,
一边上的任意一点,  于点
于点  ,那么
,那么  ( )
( )
 为
为 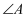 一边上的任意一点,
一边上的任意一点,  于点
于点  ,那么
,那么  ( )
( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F.

-
(1) 求证:
 ;
;
-
(2) 当点P在射线AD上运动时,设PA=X,是否存在实数x,使以P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,说明理由
如图,四边形ABCD与四边形AEFG是位似图形,且AC:AF=2:3,则下列结论不正确的是( )

A . 四边形ABCD与四边形AEFG是相似图形
B . AD与AE的比是2:3
C . 四边形ABCD与四边形AEFG的周长比是2:3
D . 四边形ABCD与四边形AEFG的面积比是4:9
随着天气的逐渐炎热(如图1),遮阳伞在我们的日常生活中随处可见.如图2所示,遮阳伞立柱OA垂直于地面,当将遮阳伞撑开至OD位置时,测得∠BOD=45°,当将遮阳伞撑开至OE位置时,测得∠BOE=60°,且此时遮阳伞边沿上升的竖直高度BC为30cm,求当遮阳伞撑开至OE位置时,伞下半径EC的长.
(结果精确到0.1cm,参考值  ≈2.449).
≈2.449).

如图的平面直角坐标系中,A点的坐标是(4,3)。图1中,点P为正方形ABCD的中心,顶点C、D分别在y轴和x轴的正半轴上,则OP=;图2中,点P为正△ABC的中心,顶点B、C分别在y轴和x轴的正半轴上,则OP=。

若反比例函数的图象经过点(﹣2,3)和(m,2),则m的值为
如图,在y轴正半轴上依次截取OA1=A1A2=A2A3=…=An﹣1An(n为正整数),过点A1 , A2 , A3 , …,An分别作y轴的垂线,与反比例函数y= (x>0)交于P1 , P2 , P3 , …,Pn , 连接P1P2 , P2P3 , P3P4 , …,Pn﹣1Pn , 得梯形A1A2P2P1 , A2A3P3P2 , A3A4P4P3 , …,AnAn+1Pn+1Pn , 设其面积分别为S1 , S2 , S3 , …,Sn , 则Sn=( )
(x>0)交于P1 , P2 , P3 , …,Pn , 连接P1P2 , P2P3 , P3P4 , …,Pn﹣1Pn , 得梯形A1A2P2P1 , A2A3P3P2 , A3A4P4P3 , …,AnAn+1Pn+1Pn , 设其面积分别为S1 , S2 , S3 , …,Sn , 则Sn=( )
 (x>0)交于P1 , P2 , P3 , …,Pn , 连接P1P2 , P2P3 , P3P4 , …,Pn﹣1Pn , 得梯形A1A2P2P1 , A2A3P3P2 , A3A4P4P3 , …,AnAn+1Pn+1Pn , 设其面积分别为S1 , S2 , S3 , …,Sn , 则Sn=( )
(x>0)交于P1 , P2 , P3 , …,Pn , 连接P1P2 , P2P3 , P3P4 , …,Pn﹣1Pn , 得梯形A1A2P2P1 , A2A3P3P2 , A3A4P4P3 , …,AnAn+1Pn+1Pn , 设其面积分别为S1 , S2 , S3 , …,Sn , 则Sn=( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
抛物线y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=  在同一平面直角坐标系内的图象大致为( )
在同一平面直角坐标系内的图象大致为( )
 在同一平面直角坐标系内的图象大致为( )
在同一平面直角坐标系内的图象大致为( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在我们日常生活中存在很多较小的或眼睛不易辨清的物体,利用放大镜“放大”,可以使人看得更清楚.如图,利用放大镜可以看清辣椒表面的纹路,这种图形的变换是( )

A . 平移变换
B . 旋转变换
C . 轴对称变换
D . 相似变换
京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).

某游乐场一转角滑梯如图所示,滑梯立柱  均垂直于地面,点
均垂直于地面,点  在线段
在线段  上.在
上.在  点测得点
点测得点  的仰角为
的仰角为  ,点
,点  的俯角也为
的俯角也为  ,测得
,测得  间的距离为10米,立柱
间的距离为10米,立柱  高30米.求立柱
高30米.求立柱  的高(结果保留根号).
的高(结果保留根号).
 均垂直于地面,点
均垂直于地面,点  在线段
在线段  上.在
上.在  点测得点
点测得点  的仰角为
的仰角为  ,点
,点  的俯角也为
的俯角也为  ,测得
,测得  间的距离为10米,立柱
间的距离为10米,立柱  高30米.求立柱
高30米.求立柱  的高(结果保留根号).
的高(结果保留根号).
在同一时刻太阳光线是平行的,如果高1.5米的测杆影长3米,那么此时影长36米的旗杆的高度为( )
A . 18米
B . 12米
C . 15米
D . 20米
正方形的A1B1P1P2顶点P1、P2在反比例函数y=  (x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2 , 顶点P3在反比例函数y=
(x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2 , 顶点P3在反比例函数y=  (x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为.
(x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为.

已知  ,且相似比为
,且相似比为 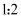 ,则
,则 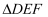 与
与  的面积比为.
的面积比为.
 ,且相似比为
,且相似比为 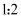 ,则
,则 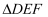 与
与  的面积比为.
的面积比为.
如图, 为
为 的直径,C是
的直径,C是 上一点,过点C作
上一点,过点C作 的切线交
的切线交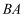 的延长线于点D,连接
的延长线于点D,连接 .
.
 为
为 的直径,C是
的直径,C是 上一点,过点C作
上一点,过点C作 的切线交
的切线交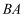 的延长线于点D,连接
的延长线于点D,连接 .
. 
-
(1) 求证:
 ;
;
-
(2) 当
 时,①求
时,①求 ;
;②若
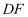 平分
平分 , 交
, 交 于点F,
于点F, , 求
, 求 半径.
半径.
如图,已知△ABC内接于⊙O,D为  上一点,
上一点,  ,过点D作⊙O的切线,分别与AB,AC的延长线相交于点E,点F,OD与BC相交于点G,连接OC,CD,BD,则下列结论:①∠ODB+
,过点D作⊙O的切线,分别与AB,AC的延长线相交于点E,点F,OD与BC相交于点G,连接OC,CD,BD,则下列结论:①∠ODB+  ∠DOC=90°;②∠BAC=2∠CBD;③AB⋅CF=AC⋅BE;④若∠BAC=60°,则OG=DG.其中正确的是(填写所有正确结论的序号)
∠DOC=90°;②∠BAC=2∠CBD;③AB⋅CF=AC⋅BE;④若∠BAC=60°,则OG=DG.其中正确的是(填写所有正确结论的序号)
 上一点,
上一点,  ,过点D作⊙O的切线,分别与AB,AC的延长线相交于点E,点F,OD与BC相交于点G,连接OC,CD,BD,则下列结论:①∠ODB+
,过点D作⊙O的切线,分别与AB,AC的延长线相交于点E,点F,OD与BC相交于点G,连接OC,CD,BD,则下列结论:①∠ODB+  ∠DOC=90°;②∠BAC=2∠CBD;③AB⋅CF=AC⋅BE;④若∠BAC=60°,则OG=DG.其中正确的是(填写所有正确结论的序号)
∠DOC=90°;②∠BAC=2∠CBD;③AB⋅CF=AC⋅BE;④若∠BAC=60°,则OG=DG.其中正确的是(填写所有正确结论的序号) 
如图,AD是△ABC的中线,E是AD上的一点,且AE=  AD,CE交AB于点F.若AF=1.2cm,则AB=
AD,CE交AB于点F.若AF=1.2cm,则AB=
 AD,CE交AB于点F.若AF=1.2cm,则AB=
AD,CE交AB于点F.若AF=1.2cm,则AB= 
最近更新
- 长时间运动引起机体缺氧时,血液pH的变化趋势、引起pH变化的物质、能起缓冲作 用的物质分别是 () A.降低、CO2
- 下列过程未体现生物膜信息传递功能的是 A.蔗糖溶液使洋葱表皮细胞发生质壁分离 B.抗原刺激引发记忆细胞增殖分化 C.胰岛
- 如图所示电路中,电源电压保持不变,闭合开关S后,将滑动变阻器R2的滑片P向右移动,在此过程中( )A.电流表A示数
- 解放战争中中国能够迅速取胜的原因有①中国的坚强领导 ②国民党军队的腐败涣散 ③人民群众的支
- 右边漫画《如此“助”农》,告诉我们 A.有权威的政府能够得到人民的信任和支持 B.有权威的政府必须自觉接受人民群众
- ______satisfiesme is________we can pay for all this. A.
- 如下图所示,图中圆圈表示某条纬线,A点为晨昏圈与纬线圈的切点。据此回答下题。若A点的地理坐标为(80°N,150°W),
- 某同学以新鲜洋葱鳞片叶白色内表皮为材料,经不同处理和染色剂染色。用高倍镜观察。下列有关描述正确的是 A.经吡罗红甲基绿染
- 向100g质量分数为20%的NaCl溶液中加入3gNaCl固体和12g水,使其完全溶解,所得溶液中NaCl的质量分数是(
- 对王安石的《登飞来峰》赏析不正确的一项是( )登飞来峰王安石飞来山上千寻塔,闻说鸡鸣见日升。不畏浮云遮望眼,自缘
- 对某动物细胞进行荧光标记实验,如下示意图所示,其基本过程:①用某种荧光染料标记该动物细胞,细胞表面出现荧光斑点。②用激光
- 如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同样乙已经助攻冲到B点.有两种射门方式:第一
- The head teacher would take Mary’s recent illness into
- 宋代官员中,有三分之一以上来自平民家庭,这是因为当时推行的选官制度是
- 已知:tan(-2α)=m(m≠0),则cot(2α+)的值为___________.
- 台湾作家林清玄写了一首禅诗:白鹭立雪,愚人看鹭,聪明见雪,智者观白。这首诗蕴含的哲理是 ①不同的人对同一事物有不同的看法
- 2007年是美国宪法制定220周年、十月革命胜利90周年和抗日战争爆发70周年。下列各项中,2007年为其签订60周年并
- 小明和他的父亲乘坐出租车在平直的公路上匀速行驶,下图为他们乘车到目的地时的车费发票,请你帮助小明解决如下问题:⑴出租车行
- 11.--- Do you have any idea why the bus – drivers are on str
- 陶渊明的《桃花源记》中“_______________,_______________”体现了《大道之行也》中的“老有所



