如图，在△ABC中点D、E分别在边AB、AC上，请添加一个条件： ，使△ABC∽△AED．

 

一些完全相同的小正方形搭成一个几何体，这个几何体从正面和左面看所得的平面图形均如图所示，小正方体的块数可能有（    ）

已知反比例函数y= 的图象经过点（3a，a），则反比例函数的图象在（   ）

如图所示的几何体是由六个相同的小正方体组合而成的，则从它左边看到的平面图形是（     ）

若△ABC与△DEF的相似比是3：2，△DEF的最长边是6cm，那么△ABC的最长边是（　　）

已知：在矩形ABCD中，E为AB边的中点，F为边AD上的动点，过点F作EF的垂线交DC于点H ， 以EF为直径作半圆O ．

如图是正方体的一个平面展开图，如果原正方体上前面的字为“友”，则后面的字为（   ）

如果圆锥的侧面积为20πcm² ， 它的母线长为5cm，那么此圆锥的底面半径的长等于（   ）

我市某蔬菜生产基地在气温较低时，用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种．如图是某天恒温系统从开启到关闭及关闭后，大棚内温度y(℃)随时间x (小时)变化的函数图象，其中BC段是双曲线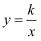的一部分．请根据图中信息解答下列问题：

（1）恒温系统在这天保持大棚内温度18℃的时间有多少小时？
（2）求k的值；
（3）当x=16时，大棚内的温度约为多少度？

一次函数y=ax+b（a≠0）的图象与反比例函数y= （k≠0）的图象相交于A，B两点，与y轴交于点C，与x轴交于点D，点D的坐标为（﹣1，0），点A的横坐标是1，tan∠CDO=2．过点B作BH⊥y轴交y轴于H，连接AH．

如图，游客在点A处坐缆车出发，沿A﹣B﹣D的路线可至山顶D处，假设AB和BD都是直线段，且AB＝BD＝600m，α＝75°，β＝45°，求DE的长．

（参考数据：sin75°≈0.97，cos75°≈0.26， ≈1.41）

将一张边长为30㎝的正方形纸片的四角分别剪去一个边长为xcm的小正方形，然后折叠成一个无盖的长方体.当ｘ取下面哪个数值时，长方体的体积最大（）

如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数y= 的图象上，若点A的坐标为（4，﹣2），则k的值为．

AB是⊙O的弦，OM⊥AB，垂足为M，连接OA.若△AOM中有一个角是60°，OM＝ ，则弦AB的长为.

 

如图，△AOB三个顶点的坐标分别为A（8，0），O（0，0），B（8，﹣6），点M为OB的中点．以点O为位似中心，把△AOB缩小为原来的 ，得到△A′O′B′，点M′为O′B′的中点，则MM′的长为．

关于反比例函数y= ，下列说法中正确的是（    ）

圆锥的侧面展开图是一个弧长为12π的扇形，则这个圆锥底面积的半径是（　　）

如图，斜坡AB长130米，坡度i=1：2.4，BC⊥AC，现在计划在斜坡AB的中点D处挖去部分坡体修建一个平行于水平线CA的平台DE和一条新的斜坡BE，若斜坡BE的坡角为30°，则平台DE的长约为（   ）（精确到0.1米，参考数据： ≈1.41， ≈1.73， ≈2.45）

如图，在等腰△ABC中，AB=BC。CD∥AB，点D在点C的右侧，点A，E关于直线BD对称，CE交BD于点F，AE交DB延长线于点G。