九年级(初三)数学下学期下册试题
若点  在反比例函数
在反比例函数  的图象上,则
的图象上,则  的大小关系是.
的大小关系是.
 在反比例函数
在反比例函数  的图象上,则
的图象上,则  的大小关系是.
的大小关系是.
回顾:用数学的思维思考

-
(1) 如图1,在△ABC中,AB=AC.
①BD,CE是△ABC的角平分线.求证:BD=CE.
②点D,E分别是边AC,AB的中点,连接BD,CE.求证:BD=CE.
(从①②两题中选择一题加以证明)
-
(2) 猜想:用数学的眼光观察
经过做题反思,小明同学认为:在△ABC中,AB=AC,D为边AC上一动点(不与点A,C重合).对于点D在边AC上的任意位置,在另一边AB上总能找到一个与其对应的点E,使得BD=CE.进而提出问题:若点D,E分别运动到边AC,AB的延长线上,BD与CE还相等吗?请解决下面的问题:
如图2,在△ABC中,AB=AC,点D,E分别在边AC,AB的延长线上,请添加一个条件(不再添加新的字母),使得BD=CE,并证明.
-
(3) 探究:用数学的语言表达
如图3,在△ABC中,AB=AC=2,∠A=36°,E为边AB上任意一点(不与点A,B重合),F为边AC延长线上一点.判断BF与CE能否相等.若能,求CF的取值范围;若不能,说明理由.
将两个长方体如图放置,则所构成的几何体的主视图可能是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,每个小方格都是边长为1个单位的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).

-
(1) 若D(2,3),请在网格图中画一个格点△DEF,使△DEF ∽△ABC,且相似比为2∶1;
-
(2) 求△ABC中AC边上的高;
-
(3) 若△ABC外接圆的圆心为P,则点P的坐标为
计算:sin30°+cos45°﹣tan30°•sin60°.
在△ABC中,∠A=120°,AB=2,AC=4,则sinB的值是.
如图,为测量瀑布AB的高度,测量人员在瀑布对面山上的D点处测得瀑布顶端A点的仰角是30°,测得瀑布底端B点的俯角是10°,AB与水平面垂直.又在瀑布下的水平面测得CG=27.0m,GF=17.6m(注:C、G、F三点在同一直线上,CF⊥AB于点F),斜坡CD=20.0m,坡角∠ECD=40°.求:

参考数据:  ≈1.73,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18
≈1.73,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18
-
(1) 测量点D距瀑布AB的距离(精确到0.1m).
-
(2) 瀑布AB的高度(精确到0.1m).
如图,已知抛物线 经过△ABC的三个顶点,其中点A(0,1),点B(-9,10),AC∥x轴,点P是直线AC下方抛物线上的一个动点.
经过△ABC的三个顶点,其中点A(0,1),点B(-9,10),AC∥x轴,点P是直线AC下方抛物线上的一个动点.
 经过△ABC的三个顶点,其中点A(0,1),点B(-9,10),AC∥x轴,点P是直线AC下方抛物线上的一个动点.
经过△ABC的三个顶点,其中点A(0,1),点B(-9,10),AC∥x轴,点P是直线AC下方抛物线上的一个动点.
-
(1) 求抛物线的解析式.
-
(2) 过点P与y轴平行的直线l与直线AB,AC分别交于点E,F,当点P在何处时,四边形AECP的面积最大,最大是多少?
-
(3) 当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C,P,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.
关于x的一元二次方程x2﹣  x+cosα=0有两个相等的实数根,则锐角a等于( )
x+cosα=0有两个相等的实数根,则锐角a等于( )
 x+cosα=0有两个相等的实数根,则锐角a等于( )
x+cosα=0有两个相等的实数根,则锐角a等于( )
A . 0°
B . 30°
C . 45°
D . 60°
如图,D、E是△ABC边AB上的点,F、G分别是边AC、BC上的点,且满足AD=DE=EB,DF∥BC,GE∥AC.

-
(1) 求证:FG∥AB;
-
(2) 设
 =
=  ,
,  =
=  ,请用向量
,请用向量  ,
,  表示
表示  .
.
如图,一个圆锥的高为  cm,侧面展开图是半圆.求:
cm,侧面展开图是半圆.求:
 cm,侧面展开图是半圆.求:
cm,侧面展开图是半圆.求: 
-
(1) 圆锥的母线长与底面半径之比;
-
(2) 求∠BAC的度数;
-
(3) 圆锥的侧面积(结果保留π).
如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段 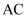 的长为.
的长为.
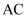 的长为.
的长为. 
如图,Rt△AOB中,∠AOB=90°,且点A在反比例函数  的图象上,点B在反比例函数
的图象上,点B在反比例函数  的图象上,则tanB的值是( )
的图象上,则tanB的值是( )
 的图象上,点B在反比例函数
的图象上,点B在反比例函数  的图象上,则tanB的值是( )
的图象上,则tanB的值是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图所示, 在函数
在函数 (x>0)的图象上,△OP1A1 , △P2A1A2 , △P3A2A3 , ……,△PnAn-1An……都是等腰直角三角形,斜边OA1 , A1A2 , ……,An-1An , 都在x轴上,则y1 + y2 + … + yn =.
(x>0)的图象上,△OP1A1 , △P2A1A2 , △P3A2A3 , ……,△PnAn-1An……都是等腰直角三角形,斜边OA1 , A1A2 , ……,An-1An , 都在x轴上,则y1 + y2 + … + yn =.
 在函数
在函数 (x>0)的图象上,△OP1A1 , △P2A1A2 , △P3A2A3 , ……,△PnAn-1An……都是等腰直角三角形,斜边OA1 , A1A2 , ……,An-1An , 都在x轴上,则y1 + y2 + … + yn =.
(x>0)的图象上,△OP1A1 , △P2A1A2 , △P3A2A3 , ……,△PnAn-1An……都是等腰直角三角形,斜边OA1 , A1A2 , ……,An-1An , 都在x轴上,则y1 + y2 + … + yn =.
若△ABC与△A′B′C′相似,∠A=55°,∠B=100°,那么∠C′的度数是( )
A . 55°
B . 100°
C . 25°
D . 不能确定
如图,在矩形  中,
中,  ,E为
,E为  上一点,将
上一点,将  沿
沿  折叠,使点C正好落在
折叠,使点C正好落在  边上的F处,作
边上的F处,作  的平分线交
的平分线交  于N,交
于N,交  的延长线于M,若
的延长线于M,若  ,则
,则  的长为.
的长为.
 中,
中,  ,E为
,E为  上一点,将
上一点,将  沿
沿  折叠,使点C正好落在
折叠,使点C正好落在  边上的F处,作
边上的F处,作  的平分线交
的平分线交  于N,交
于N,交  的延长线于M,若
的延长线于M,若  ,则
,则  的长为.
的长为. 
如图,A(a,b)、B(1,4)(a>1)是反比例函数y=  (x>0)图象上两点,过A、B分别作x轴、y轴的垂线,垂足分别为C、D、E、F,AE、BD交于点G.则四边形ACDG的面积随着a的增大而.(填“减小”、“不变”或“增大”)
(x>0)图象上两点,过A、B分别作x轴、y轴的垂线,垂足分别为C、D、E、F,AE、BD交于点G.则四边形ACDG的面积随着a的增大而.(填“减小”、“不变”或“增大”)
 (x>0)图象上两点,过A、B分别作x轴、y轴的垂线,垂足分别为C、D、E、F,AE、BD交于点G.则四边形ACDG的面积随着a的增大而.(填“减小”、“不变”或“增大”)
(x>0)图象上两点,过A、B分别作x轴、y轴的垂线,垂足分别为C、D、E、F,AE、BD交于点G.则四边形ACDG的面积随着a的增大而.(填“减小”、“不变”或“增大”) 
如图,已知△ABC中,AB=AC=5,BC=8.则cosB的值是( )

A . 1.25
B . 0.8
C . 0.6
D . 0.625
如图,在Rt△ABC中,∠C=90°,D是BC边上一点,AC=2,CD=1,设∠CAD=α.

-
(1) 求sinα、cosα、tanα的值;
-
(2) 若∠B=∠CAD,求BD的长.
如果等腰三角形的面积为6,底边长为x,底边上的高为y,则y与x的函数关系式为( )
A . y=  B . y=
B . y=  C . y=
C . y= 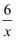 D . y=
D . y= 
 B . y=
B . y=  C . y=
C . y= 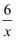 D . y=
D . y= 
最近更新
- 光与平面镜成300角射在平面镜上,如图所示,画出它的反射光线,并标明反射角的大小。
- 比较阅读下面两段文言短文,回答下列问题。(13分)【甲】于是入朝见威王,曰:“臣诚知不如徐公美。臣之妻私臣,臣之妾畏臣,
- 材料一 “夫农者,国之本,本立然后可以议太平。若不由兹,而云太平者,谬矣。” ──《旧唐书》 材料二 中国农村原本是
- 已知,若成等比,成等差,则_____________.
- 下列实验操作正确的是
- 根据提示,在划线处填上恰当的诗句。 杜甫是唐代大诗人,他见证了唐王朝由盛转衰的历史。青年时代,身处开元盛世的他有着“
- 新疆人民的生产和生活用水主要来自( ) A.降水 B.河水
- 函数f(x)=2x2﹣2x的单调递增区间是() A.(﹣∞,1] B.[1,+∞) C.(﹣∞,2]
- “环境是我家,爱护靠大家!”下列标志中,与保护环境无关的是
- 1929年《大公报》刊登一则《离婚法论》卖书广告,称:“本书共二十余万言,有学说、有法条、有判例、有轶闻,足为解决离婚问
- 阅读图文资料,完成下列问题。 (1)读图1,描述秘鲁年降水量分布规律。(2分) (2)说出图2中洋流流向。说明洋流对秘
- 2004年12月14日,据来自卫生部艾滋病预防与控制中心的消息,虽然我国艾滋病疫苗研究工作尚处于实验室阶段,但这项研究已
- (09年山东省实验中学综合测试理)如果的展开式中含有非零常数项,则正 整数的最小值为__________.
- Pandas are our Chinese treasure. They feed on(主食) __________
- 4. 下图所示为古代中国某朝代中枢机构示意图。该朝代是 A.秦 B.汉 C.宋
- 下列各句中,没有语病的一句是 A.如果不重视网络道德建设,一些道德败坏现象及消极落后思想就可通过网络影响人们的身心健康,
- 用NA表示阿伏加德罗常数的值,下列说法中正确的是( ) A.1 mol N2所含有的原子数为NA B.标准状况下,
- 下列关于元素周期表的说法不正确的是() A.除零族元素外,非金属元素全部都是主族元素 B.第三周期非金属元素含氧酸的酸性
- 水是生命之源,保护水资源,防止水污染是每个公民和全社会的责任.下列做法有利于防止水资源污染的是①农业生产中要合理使用农药
- 下列反应中属于吸热反应的是 A.铝跟盐酸反应 B.Ba(OH)2•8H2O晶体与NH4Cl晶体的反应 C.盐酸与



