九年级(初三)数学下学期下册试题
如图,在  中,
中,  ,
,  ,
,  ,动点P从点B开始沿边BA,AC向点C以
,动点P从点B开始沿边BA,AC向点C以  的速度移动,动点Q从点B开始沿边BC向点C以
的速度移动,动点Q从点B开始沿边BC向点C以  的速度移动,设
的速度移动,设  的面积为
的面积为  运动时间为
运动时间为  ,则下列图象能反映y与x之间关系的是( )
,则下列图象能反映y与x之间关系的是( )
 中,
中,  ,
,  ,
,  ,动点P从点B开始沿边BA,AC向点C以
,动点P从点B开始沿边BA,AC向点C以  的速度移动,动点Q从点B开始沿边BC向点C以
的速度移动,动点Q从点B开始沿边BC向点C以  的速度移动,设
的速度移动,设  的面积为
的面积为  运动时间为
运动时间为  ,则下列图象能反映y与x之间关系的是( )
,则下列图象能反映y与x之间关系的是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知两点P1(x1 , y1)、P2(x2、y2)在反比例函数y=  的图象上,当x1>x2>0时,下列结论正确的是( )
的图象上,当x1>x2>0时,下列结论正确的是( )
 的图象上,当x1>x2>0时,下列结论正确的是( )
的图象上,当x1>x2>0时,下列结论正确的是( )
A . 0<y1<y2
B . 0<y2<y1
C . y1<y2<0
D . y2<y1<0
如图所示,正方形EFGH是由正方形ABCD经过位似变换得到的,点O是位似中心,E , F , G , H分别是OA , OB , OC , OD的中点,则正方形EFGH与正方形ABCD的面积比是( )

A . 1:6
B . 1:5
C . 1:4
D . 1:2
如图所示的几何体的俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某兴趣小组用高为1米的仪器测量建筑物CD的高度.如示意图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为∠β=30  ,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为∠ɑ=60
,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为∠ɑ=60  .测得A,B之间的距离为4米,建筑物CD的高度为 .
.测得A,B之间的距离为4米,建筑物CD的高度为 .
 ,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为∠ɑ=60
,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为∠ɑ=60  .测得A,B之间的距离为4米,建筑物CD的高度为 .
.测得A,B之间的距离为4米,建筑物CD的高度为 . 
已知点P(1,2)在反比例函数y= 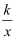 的图象上,过P作x轴的垂线,垂足为M,则△OPM的面积为( )
的图象上,过P作x轴的垂线,垂足为M,则△OPM的面积为( )
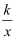 的图象上,过P作x轴的垂线,垂足为M,则△OPM的面积为( )
的图象上,过P作x轴的垂线,垂足为M,则△OPM的面积为( )
A . 2
B . 4
C . 8
D . 1
下列说法错误的是( )
A . 两个等边三角形一定相似
B . 两个等腰三角形一定相似
C . 两个等腰直角三角形一定相似
D . 两个全等三角形一定相似
如图,小颖为测量学校旗杆AB的高度,她在E处放置一块镜子,然后退到C处站立,刚好从镜子中看到旗杆的顶部B.已知小颖的眼睛D离地面的高度CD=1.5m,她离镜子的水平距离CE=0.5m,镜子E离旗杆的底部A处的距离AE=2m,且A,C,E三点在同一水平直线上,则旗杆AB的高度为( )

A . 4.5m
B . 4.8m
C . 5.5m
D . 6 m
在 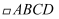 中,
中, 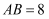 ,
,  ,
, 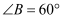 ,动点
,动点  在边
在边  上,连接
上,连接  .
.
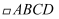 中,
中, 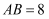 ,
,  ,
, 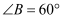 ,动点
,动点  在边
在边  上,连接
上,连接  .
. 
-
(1) 如图1,将
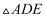 沿着
沿着  所在直线折叠,得到
所在直线折叠,得到  ,点
,点  的对应点是
的对应点是  .
. ①如图2,当点
 落在
落在  边上时线段
边上时线段  的长度是,并判断四边形
的长度是,并判断四边形  的形状,请说明理由;
的形状,请说明理由;②当
 时,线段
时,线段  的长度是;
的长度是; -
(2) 如图,将四边形
 沿着
沿着  所在直线折叠,得到四边形
所在直线折叠,得到四边形  ,其中点
,其中点  ,
,  的对应点是
的对应点是 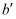 ,
, 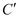 ,当
,当  经过点
经过点  时,请直接写出线段
时,请直接写出线段  的长度.
的长度.
如图,线段CD两个端点的坐标分别为C(4,4),D(6,2),以原点O为位似中心,在第一象限内将线段CD缩小为原来的一半后得到线段AB,则端点A的坐标为( )

A . (2,2)
B . (3,3)
C . (3,1)
D . (4,1)
如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3).双曲线y=  (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.

-
(1) 求k的值及点E的坐标;
-
(2) 若点F是OC边上一点,且△FBC∽△DEB,求直线FB的解析式.
如图,在白炽灯下方有一个乒乓球,当乒乓球越接近灯泡时,它在地面上影子的变化情况为(填“越小”或“越大”,“不变”)

如图,点A的坐标为(1,2),AB⊥x轴于点B,将△AOB绕点A逆时针旋转90°得到△ACD,双曲线y=  (x>0)恰好经过点C,交AD于点E,则点E的坐标为.
(x>0)恰好经过点C,交AD于点E,则点E的坐标为.

如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.

-
(1) 求证:∠DAC=∠DCE;
-
(2) 若AB=2,sin∠D=
 ,求AE的长.
,求AE的长.
九年级活动小组计划利用所学的知识测量操场旗杆高度.测量方案如下:如图,小卓在小越和旗杆之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C,镜子不动,小卓看着镜面上的标记,他来回走动,走到点D时看到旗杆顶端点A在镜面中的像与镜面上的标记点C重合,这时测得小卓眼睛与地面的高度ED=1.5米,CD=1米,然后在阳光下,小越从D点沿DM方向走了15.8米到达F处此时旗杆的影子顶端与小越的影子顶端恰好重合,测得FG=1.6米,FH=3.2米,已知AB⊥BM,ED⊥BM,GF⊥BM若测量时所使用的平面镜的厚度忽略不计,请你根据图中提供的相关信息求出旗杆的高AB.

如图,点D在△ABC的边AB上,∠ACD=∠B,AD=6cm,DB=8cm,求:AC的长.

计算:(﹣1)2022+ ﹣4sin45°+|﹣2|.
﹣4sin45°+|﹣2|.
 ﹣4sin45°+|﹣2|.
﹣4sin45°+|﹣2|.
抛物线  与x轴交于A,B两点(点A在点B的左边),与y轴正半轴交于点C.
与x轴交于A,B两点(点A在点B的左边),与y轴正半轴交于点C.
 与x轴交于A,B两点(点A在点B的左边),与y轴正半轴交于点C.
与x轴交于A,B两点(点A在点B的左边),与y轴正半轴交于点C. 
-
(1) 如图1,若
 ,
,  ,
, ①求抛物线
 的解析式;
的解析式;②Р为抛物线上一点,连接
 、
、  ,若
,若  ,求点P的坐标;
,求点P的坐标; -
(2) 如图2,D为x轴下方抛物线上一点,连
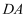 ,
,  ,若
,若  ,求点D的纵坐标.
,求点D的纵坐标.
如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,现从山顶A到河对岸点C拉一条笔直的缆绳AC,如果AC是120米,求河宽CD的长?

计算:2sin30°+(π﹣3.14)0+|1﹣  |+(﹣1)2017 .
|+(﹣1)2017 .
 |+(﹣1)2017 .
|+(﹣1)2017 .
最近更新
- 下面是几个同学对有关蛋白质和核酸之间关系的总结,你认为其中错误的是A.在同一生物体内,不同的体细胞核中DNA分子是相同的
- 下列关于生物体结构和功能的叙述,正确的是( ) A.没有叶绿体的细胞都不能进行光合作用 B.没有线粒体的
- 阅读下列材料 材料一 夏、商、周、汉封建(分封)而延,秦郡邑而促(短促)。 材料二 秦有天下……不数载而天下大坏,其
- 阅读下面这首清诗,完成①~③题。(10分) 咏笼莺①(清)纳兰性德 何处金衣客,栖栖翠幕中。有心惊晓梦,无计啭春风。 漫
- 方程y=k(x+4)表示() A.过点(-4,0)的一切直线 B.过点(4,0)的一切直线 C.过点(-4,0)且不垂直
- 如果茎a侧(长得慢的一侧)生长素浓度在A点以下范围内,则 对b侧(长得快的一侧)生长素浓度范围的描述较为准确的是A.在O
- 美国细胞生物学家威尔逊(E. B.Wilson)曾经说过:“每一个生物科学问题的答案都必须在细胞中寻找”。他作出这一结论
- 古代诗歌阅读(16分) 鹧鸪天 苏轼 林断山明竹隐墙,乱蝉衰草小池塘。翻空白鸟时时见,照水红蕖细细香。 村舍外,
- 有关A、B两河段的叙述。错误的是 A.A河段主要表现为侵蚀作用
- (06全国卷Ⅰ)下列关于动物细胞培养的叙述,正确的是 A.培养中的人效应T细胞能产生单克隆抗体 B.培养中的
- 阅读下列材料 以下材料反映了工业革命在一些方面的影响 材料一 根据1801年首次普查,该郡(英国的约克郡)只有15个城
- 下列物质属于芳香烃,但不是苯的同系物的是()
- 读冬季某区域等压线图,据此回答下列各小题.图中等压线数值排列正确的是 A.P3>P2>P1
- 下列各项中,加点字注音全错的一项是()A.躯壳qiào 香菌jùn 酵jiào母 鞠jū躬尽瘁B.独角jué戏 累léi
- 潮湿的氯气、新制的氯水、次氯酸钠溶液、漂白粉溶液均能使有色布条褪色,这是由于它们含有或能生成( ) A.氯气
- -- I’ll find someone to send this letter to the general hims
- 关于下列各图的说法错误的是( ) A.图甲中4是植物根尖吸收水分、无机盐的主要部位 B.图乙中
- 下列生物中,全部属于生产者的一组是( ) A.海带、梨树、酵母菌 B. 蘑菇、水绵、洋葱 C.马
- 10.如图(a),圆形线圈P静止在水平桌面上,其正上方悬挂一相同的线圈Q、P和Q其轴,Q中通有变化电流,电流随时间变化的
- 下列实验装置或操作与微粒的大小无直接关系的是 ( )



