九年级(初三)数学下学期下册试题
△ABC中,∠C=90°,sinA= , 则tanB的值为( )
, 则tanB的值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
计算:  .
.
 .
.
若两个相似多边形的相似比是2:3,则它们的面积比等于.
关于反比例函数 ,下列说法不正确的是 ( )
,下列说法不正确的是 ( )
 ,下列说法不正确的是 ( )
,下列说法不正确的是 ( )
A . 点(-2,-1)在它的图象上
B . 它的图象在第一、三象限
C . 当x>0时,y随x的增大而减小
D . 当x<0时,y随x的增大而增大
在Rt△ABC中,∠C=90°,∠B=35°,AB=7,则BC的长为( )
A .  B . 7sin55°
C . cos55°
D . tan55°
B . 7sin55°
C . cos55°
D . tan55°
 B . 7sin55°
C . cos55°
D . tan55°
B . 7sin55°
C . cos55°
D . tan55°
下列图形中,不能够折叠成正方体的有 (填序号)

公园新增设了一台滑梯,该滑梯高度AC=2米,滑梯AB的坡比是1:2(即AC:BC=1:2),则滑梯AB的长是米.

已知直线y=kx(k>0)与双曲线y=  交于点A(x1 , y1),B(x2 , y2)两点,则x1y2+x2y1的值为( )
交于点A(x1 , y1),B(x2 , y2)两点,则x1y2+x2y1的值为( )
 交于点A(x1 , y1),B(x2 , y2)两点,则x1y2+x2y1的值为( )
交于点A(x1 , y1),B(x2 , y2)两点,则x1y2+x2y1的值为( )
A .  B .
B .  C . 0
D . 9
C . 0
D . 9
如图,在平面直角坐标系xOy中,一次函数y=﹣x的图象与反比例函数y=  (x<0)的图象相交于点A(﹣4,m).
(x<0)的图象相交于点A(﹣4,m).
 (x<0)的图象相交于点A(﹣4,m).
(x<0)的图象相交于点A(﹣4,m). 
-
(1) 求反比例函数y=
 的解析式;
的解析式;
-
(2) 若点P在x轴上,AP=5,直接写出点P的坐标.
如图,在Rt△ABC中,∠C=90°,AB=10,AC=6,则sinB等于 .

已知圆锥的底面半径为 , 母线长为
, 母线长为 , 则这个圆锥的侧面积是(结果保留
, 则这个圆锥的侧面积是(结果保留 ).
).
 , 母线长为
, 母线长为 , 则这个圆锥的侧面积是(结果保留
, 则这个圆锥的侧面积是(结果保留 ).
).
如图,直线  ,直线AC交
,直线AC交  于点A,B,C,直线DF交
于点A,B,C,直线DF交  于点D,E,F.若
于点D,E,F.若  ,则
,则  的值为( )
的值为( )
 ,直线AC交
,直线AC交  于点A,B,C,直线DF交
于点A,B,C,直线DF交  于点D,E,F.若
于点D,E,F.若  ,则
,则  的值为( )
的值为( ) 
A .  B .
B .  C .
C . 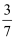 D .
D . 
 B .
B .  C .
C . 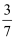 D .
D . 
如图,∠APD=90°,AP=PB=BC=CD,则下列结论成立的是( )

A . ΔPAB∽ΔPDA
B . ΔABC∽ΔDCA
C . ΔPAB∽ΔPCA
D . ΔABC∽ΔDBA
如图,是由一些大小相同的小正方体组合成的简单几同体,请在下面方格纸中分别画出从它的左面和上面看到的形状图.

如图,D为△ABC的边AC上的一点,若要使△ABD与△ACB相似,可添加一个条件:.

对于反比例函数  ,当自变量x的值从3增加到6时,函数值减少了1,则函数的解析式为( )
,当自变量x的值从3增加到6时,函数值减少了1,则函数的解析式为( )
 ,当自变量x的值从3增加到6时,函数值减少了1,则函数的解析式为( )
,当自变量x的值从3增加到6时,函数值减少了1,则函数的解析式为( )
A .  B .
B .  C .
C . 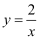 D .
D . 
 B .
B .  C .
C . 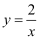 D .
D . 
5个棱长为1的正方体组成如图的几何体.

-
(1) 该几何体的体积是(立方单位),表面积是(平方单位).
-
(2) 给几何体从正面看和从左边看分别能得到什么平面图形,把它们画出来.
如图所示的几何体的俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
计算:
-
(1)

-
(2)

【阅读新知】
三角形中任何一边的平方等于其它两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.
即:如图1,.

在△ABC中,已知AB=c,BC=a,CA=b,则有:
a2=b2+c2﹣2bccosA,b2=a2+c2﹣2accosB,c2=a2+b2﹣2abcosC
利用这个正确结论可求解下列问题:
例在△ABC中,已知a=2  ,b=2
,b=2  ,c=
,c=  ,求∠A.
,求∠A.
解:∵a2=b2+c2﹣2bccosA,
cosA=  =
=  =
=  .
.
∴∠A=60°.
【应用新知】
-
(1) 选择题:在△ABC中,已知b=ccosA,a=csinB,那么△ABC是( ).A . 等边三角形 B . 等腰三角形 C . 等腰直角三角形 D . 直角三角形
-
(2)
如图2,

某客轮在A处看港口D在客轮的北偏东50°,A处看灯塔B在客轮的北偏西30°,距离为2
 海里,客轮由A处向正北方向航行到C处时,再看港口D在客轮的南偏东80°,距离为6海里.求此时C处到灯塔B的距离.
海里,客轮由A处向正北方向航行到C处时,再看港口D在客轮的南偏东80°,距离为6海里.求此时C处到灯塔B的距离.
最近更新
- 题目:我爱我的家 要求:1.不限文体(诗歌除外)。 2.不少于600字。 3.作文中不能
- 第二次中东战争后,中东问题增加了新的复杂因素,这里的“新”是指 A、英法与埃及的矛盾激化 B、英法与
- 碘是一种人体必需的微量元素,有“智力元素”之称。人体内的碘过多和过少都会得“大脖子病”。对此卫生部决定,从2010年起将
- 中美战略与经济对话机制是和奥巴马在2009年4月共同倡导建立的,是双方推动新时期中美关系发展的一项重要举措。在2010年
- 大变革时期,标志社会生产力显著提高的是( )A、铁农具在农业、手工业生产上的使用 B、 铁
- 11.古诗文默写。(5分,每空1分) (1)落日楼头, ,江南游子。(辛弃疾《水龙吟·登建康赏心亭》) (
- 图中①是电子工业区,周围有众多的高等院校,②是石油化工区。读图完成下列各题。(1)影响电子工业区布局的主导因素是____
- 如图所示是某实验小组合作探究“凸透镜成像规律”的实验装置(足够长),实验时应先调节烛焰、凸透镜、光屏,使三者的中心在同一
- 实验室制取氧气大致可分为以下几个步骤: a将高锰酸钾装入试管,用带导管的橡皮塞塞紧试管口,并把它固定在铁架台上; b检查
- Theheadmaster suggested that a good preparation ________ ahe
- 电磁打点计时器是一种使用________(直流或交流)电源的计时仪器,它的工作电压在4~6V.当电源频率为50hz时,它
- 下列句子中,没有活用现象的一项是( ) A.园日涉以成趣。 B.或棹孤舟。 C.臣具以表闻。 D.
- (共5分)分离沸点不同但又互溶的液体混合物,常用的方法是 ;分离固液混合物的常用的方法是 ;分离两种溶解度相差很大的溶质
- 环境条件变差时对植物群落结构的影响是() A.层次不变,层次结构简单 B.层次减少,层次结构不变 C.层次减少,层次结构
- 下列植物依靠风力传播花粉的是( )A、牡丹花 B、桃花 C、玉米花
- 周王将商代贵族分封为诸侯,主要目的是( ) A.保护贵族的世袭血统 B.调和
- 下列词语中加点的字,读音完全正确的一项是 A.越俎(zǔ)代庖忧心忡忡(chōnɡ) 词清讼(sònɡ)简 飒(sà)爽
- 已知力F为两个力F1、F2的合力,如果F1和F2的夹角保持不变(两个力夹角α≤180°),则当F1、F2中的一个力增大时
- (6分)小明利用如图所示的装置探究光在平面表面的反射规律,M是一个小平面镜,E、F是两块硬纸板可以绕ON前后转动.实验时
- 随着珠三角经济的崛起,广州方言“埋单”、“打包”等餐饮用语逐渐风行全国,且发展出其本义以外的涵义。这表明( )



