九年级(初三)数学下学期下册试题
如图1,在  中,
中,  ,
,  ,点P、点Q同时从点B出发,点P以
,点P、点Q同时从点B出发,点P以  的速度沿
的速度沿  运动,终点为C,点Q以
运动,终点为C,点Q以  的速度沿
的速度沿  运动,当点P到达终点时两个点同时停止运动,设点P,Q出发t秒时,
运动,当点P到达终点时两个点同时停止运动,设点P,Q出发t秒时,  的面积为
的面积为  ,已知y与t的函数关系的图象如图
,已知y与t的函数关系的图象如图  曲线OM和MN均为抛物线的一部分
曲线OM和MN均为抛物线的一部分  ,给出以下结论:
,给出以下结论:  ;
;  曲线MN的解析式为
曲线MN的解析式为  ;
;  线段PQ的长度的最大值为
线段PQ的长度的最大值为  ;
;  若
若  与
与  相似,则
相似,则  秒
秒  其中正确的是
其中正确的是  )
)
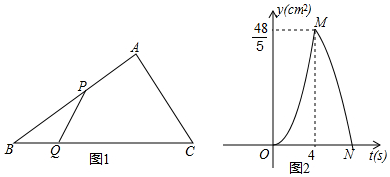
 中,
中,  ,
,  ,点P、点Q同时从点B出发,点P以
,点P、点Q同时从点B出发,点P以  的速度沿
的速度沿  运动,终点为C,点Q以
运动,终点为C,点Q以  的速度沿
的速度沿  运动,当点P到达终点时两个点同时停止运动,设点P,Q出发t秒时,
运动,当点P到达终点时两个点同时停止运动,设点P,Q出发t秒时,  的面积为
的面积为  ,已知y与t的函数关系的图象如图
,已知y与t的函数关系的图象如图  曲线OM和MN均为抛物线的一部分
曲线OM和MN均为抛物线的一部分  ,给出以下结论:
,给出以下结论:  ;
;  曲线MN的解析式为
曲线MN的解析式为  ;
;  线段PQ的长度的最大值为
线段PQ的长度的最大值为  ;
;  若
若  与
与  相似,则
相似,则  秒
秒  其中正确的是
其中正确的是  )
) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
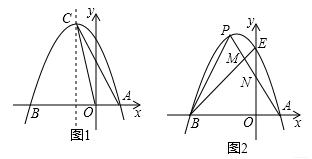
如图1,已知抛物线  过点
过点  .
.
 过点
过点  .
. 
-
(1) 求抛物线的解析式及其顶点C的坐标;
-
(2) 设点D是x轴上一点,当
 时,求点D的坐标;
时,求点D的坐标;
-
(3) 如图2.抛物线与y轴交于点E,点P是该抛物线上位于第二象限的点,线段PA交BE于点M,交y轴于点N,
 和
和  的面积分别为
的面积分别为  ,求
,求  的最大值.
的最大值.
计算:  ﹣sin30°(cos45°﹣sin60°)
﹣sin30°(cos45°﹣sin60°)
 ﹣sin30°(cos45°﹣sin60°)
﹣sin30°(cos45°﹣sin60°)
一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,已知木箱高BE=  m,斜面坡脚为30°,则木箱顶端E距离地面AC的高度EF为m。
m,斜面坡脚为30°,则木箱顶端E距离地面AC的高度EF为m。
 m,斜面坡脚为30°,则木箱顶端E距离地面AC的高度EF为m。
m,斜面坡脚为30°,则木箱顶端E距离地面AC的高度EF为m。 
某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
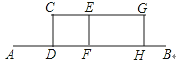
-
(1) 请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法)
-
(2) 求小明原来的速度。
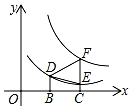
如图,△DEF的三个顶点分别在反比例函数xy=n与xy=m(x>0,m>n>0)的图象上,若DB⊥x轴于B点,FE⊥x轴于C点,若B为OC的中点,△DEF的面积为2,则m,n的关系式是( )
A . m﹣n=8
B . m+n=8
C . 2m﹣n=8
D . 2m+n=3
计算:32﹣20150+tan45°.
美丽的东昌湖是我市的一大旅游胜地.如图,湖岸的一段 长40米,
长40米, 与桥
与桥 所在的路线成
所在的路线成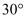 的角,小亮在B点处测得
的角,小亮在B点处测得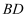 与桥
与桥 的夹角
的夹角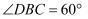 , 在点A处测得
, 在点A处测得 与平行于桥
与平行于桥 的直线之间的夹角为
的直线之间的夹角为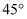 , 桥
, 桥 与湖岸
与湖岸 是垂直的.求湖岸上的路线
是垂直的.求湖岸上的路线 的长.(结果保留根号)
的长.(结果保留根号)
 长40米,
长40米, 与桥
与桥 所在的路线成
所在的路线成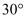 的角,小亮在B点处测得
的角,小亮在B点处测得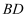 与桥
与桥 的夹角
的夹角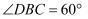 , 在点A处测得
, 在点A处测得 与平行于桥
与平行于桥 的直线之间的夹角为
的直线之间的夹角为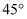 , 桥
, 桥 与湖岸
与湖岸 是垂直的.求湖岸上的路线
是垂直的.求湖岸上的路线 的长.(结果保留根号)
的长.(结果保留根号)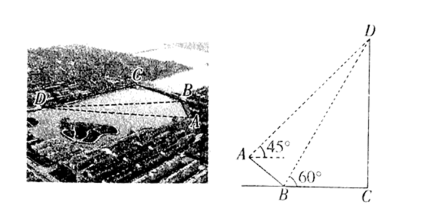
在Rt△ABC中,∠C=90°,tanA= , 则cosB的值是( )
, 则cosB的值是( )
 , 则cosB的值是( )
, 则cosB的值是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若一个圆锥的侧面展开图是一个半径为10cm,圆心角为144°的扇形,则该圆锥的底面半径为 cm.
如图,点E是矩形ABCD的边AD的中点,且BE⊥AC于点F,则下列结论中错误的是( )
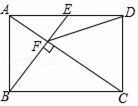
A . AF=  CF
B . ∠DCF=∠DFC
C . 图中与△AEF相似的三角形共有5个
D . tan∠CAD=
CF
B . ∠DCF=∠DFC
C . 图中与△AEF相似的三角形共有5个
D . tan∠CAD= 
 CF
B . ∠DCF=∠DFC
C . 图中与△AEF相似的三角形共有5个
D . tan∠CAD=
CF
B . ∠DCF=∠DFC
C . 图中与△AEF相似的三角形共有5个
D . tan∠CAD= 
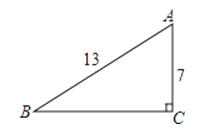
如图,在Rt△ABC中,∠C=90°,AB=13,AC=7,则cosA=
如图,在菱形  中,
中, 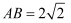 ,
, 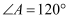 ,点P,Q,K分别为线段
,点P,Q,K分别为线段  ,
,  ,
,  上的任意一点,则
上的任意一点,则  的最小值为.
的最小值为.
 中,
中, 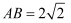 ,
, 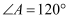 ,点P,Q,K分别为线段
,点P,Q,K分别为线段  ,
,  ,
,  上的任意一点,则
上的任意一点,则  的最小值为.
的最小值为. 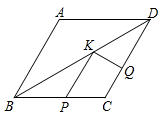
已知sinA=  ,那么锐角
,那么锐角 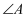 等于( )
等于( )
 ,那么锐角
,那么锐角 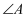 等于( )
等于( )
A . 15°
B . 30°
C . 45°
D . 60°
计算: 

如图,其左视图是矩形的几何体是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,△ABC的各个顶点都在正方形的格点上,则sinA的值为( )

A .  B .
B . 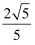 C .
C . 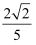 D .
D . 
 B .
B . 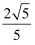 C .
C . 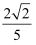 D .
D . 
如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.

-
(1) 判断直线DE与⊙O的位置关系,并说明理由;
-
(2) 若AC=3,BC=4,OA=1,求线段DE的长.
在Rt△ABC中,∠C = 90°,∠A、∠B、∠C所对的边分别为a、b、c , 下列等式中成立的是( )
A . 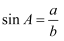 B .
B .  C .
C . 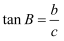 D .
D . 
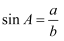 B .
B .  C .
C . 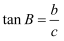 D .
D . 
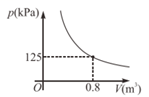
某气球内充满一定质量的气体,温度不变时,气球内气体的压强 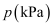 与气体的体积
与气体的体积  的关系是如图所示的反比例函数.当气球内气体的压强大于200kPa,气球就会爆炸.为了不让气球爆炸,则气球内气体的体积
的关系是如图所示的反比例函数.当气球内气体的压强大于200kPa,气球就会爆炸.为了不让气球爆炸,则气球内气体的体积 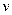 需满足的取值范围是( )
需满足的取值范围是( )
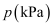 与气体的体积
与气体的体积  的关系是如图所示的反比例函数.当气球内气体的压强大于200kPa,气球就会爆炸.为了不让气球爆炸,则气球内气体的体积
的关系是如图所示的反比例函数.当气球内气体的压强大于200kPa,气球就会爆炸.为了不让气球爆炸,则气球内气体的体积 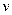 需满足的取值范围是( )
需满足的取值范围是( )
A . 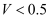 B .
B . 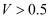 C .
C . 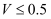 D .
D . 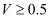
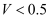 B .
B . 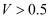 C .
C . 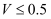 D .
D . 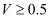
最近更新
- This seemed like money for nothing. There were millions of f
- 生物体内既能储存能量,又能为生命活动直接提供能量的物质是() A. 葡萄糖 B. 糖原 C. 三磷酸腺苷 D. 脂肪
- (09年宜昌一中10月月考文)下列四个函数中,既是上的增函数,又是以π为周期的偶函数是( ) A. B
- ThisMarch is a busy month in Shanghai. There’s a lot to do.
- 设随机变量服从正态分布,若,则实数等于 A. B. C.
- 请在“石墨、氮气、二氧化硫、甲烷、熟石灰”中选择合适的物质填空:填化学式或名称) (1)能形成硫酸型酸雨的空气污染
- 为迎合“抗震救灾”的大形势,安徽卫视2008年第二季度独家播出的励志电视剧《笑着活下去》,取得了省级卫视电视剧收视同时段
- _______differentlife today it is from ______was fifty years
- X、Y、Z为三种金属.X、Y放入稀硫酸中均放出氢气,Z与稀硫酸不反应将X放入Y(NO3)2溶液中,有Y单质析出.X、Y
- With big handbags becoming a key fashion accessory(配件)for wo
- 去南极地区进行科学考察的最佳时间是: A.每年的3月到11月 B.每年的6月到8月 C.每年的11
- 山东省环保厅正在对《山东省2013-2020年大气污染防治规划二期(2016—2017年)行动计划》征求意见。如果你要参
- 18.在下面一段文字横线处补写恰当的语句,使整段文字语意完整连贯,内容贴切,逻辑严密。每处不超过15个字。 据相关医学报
- 九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3 m,标杆与旗杆间的水平距离BD=15 m,人
- 在横线上写出古代诗文的原句。① ,各领风骚数百年。 (赵 翼《论诗》 ) ②白头吊古
- 1815年,法国与英国争夺欧洲和世界霸权地位的失败,标志着伦敦对巴黎的胜利,标志着伦敦将成为世界的经济中心,而巴黎则不再
- 下列实验事实不能作为相应观点的证据是( )选项 实验事实 观点 A 铁丝在氧气中燃烧后质量增大 化学反应前后质量守
- 如图,正方形ABCD的顶点A、D分别在x轴、y轴上,∠ADO=30°,OA=2,反比例函y=经过CD的中点M,那么k=_
- 在某地24时看到北极星的仰角是40°,这时格林尼治时间是18时,那么,这个地点的地理坐标是 ( ) A.90°E
- 下面为四幅等高线分布图,若图中等高线的数值皆由左上方向右下方递减,按要求完成下面试题。若四幅图的等高距皆为50米,比例尺



