九年级(初三)数学下学期下册试题
如图,已知:抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,点D为顶点,连接BD,CD,抛物线的对称轴与x轴交与点E.

-
(1) 求抛物线解析式及点D的坐标;
-
(2) G是抛物线上B,D之间的一点,且S四边形CDGB=4S△DGB , 求出G点坐标;
-
(3) 在抛物线上B,D之间是否存在一点M,过点M作MN⊥CD,交直线CD于点N,使以C,M,N为顶点的三角形与△BDE相似?若存在,求出满足条件的点M的坐标,若不存在,请说明理由.
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(8,n)在边AB上,反比例函数y=  (k≠0)在第一象限内的图象经过点D,E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D,E,且tan∠BOA=  .
.
 (k≠0)在第一象限内的图象经过点D,E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D,E,且tan∠BOA=  .
.
-
(1) 求反比例函数的解析式和n的值;
-
(2) 若反比例函数的图象与矩形的边BC交于点F,将矩 形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求G点的坐标.

下列各组线段中(单位:cm),成比例线段的是( )
A . 1、2、3、4
B . 1、2、2、4
C . 3、5、9、13
D . 1、2、2、3
一个几何体的主视图和左视图如图,该物体的形状是( )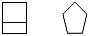
A . 四棱柱
B . 五棱柱
C . 六棱柱
D . 三棱柱
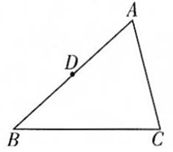
尺规作图:已知点D为△ABC的边AB的中点,用尺规在△ABC的边AC上找一点E,使 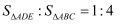 (保留作图痕迹,不写作法).
(保留作图痕迹,不写作法).
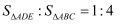 (保留作图痕迹,不写作法).
(保留作图痕迹,不写作法).
沿一张矩形纸较长两边中点将纸一分为二,所得两张矩形纸与原来的矩形纸相似,那么原来那张纸的长和宽的比是( )
A . 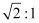 B .
B . 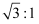 C . 2:1
D . 3:1
C . 2:1
D . 3:1
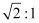 B .
B . 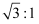 C . 2:1
D . 3:1
C . 2:1
D . 3:1
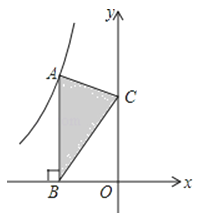
如图,点A是反比例函数y= 的图象上的一点,过点A作AB⊥x轴,垂足为B,点C为y轴上的一点,连接AC、BC,若△ABC的面积为3,则k的值是
的图象上的一点,过点A作AB⊥x轴,垂足为B,点C为y轴上的一点,连接AC、BC,若△ABC的面积为3,则k的值是
圆锥的侧面展开图是一个扇形,扇形的弧长为10π cm,扇形面积为65π cm2 , 则圆锥的高为cm.
-
(1) x2﹣2x﹣3=0
-
(2) cos45°•tan45°+
 tan30°﹣2cos60°2sin45°
tan30°﹣2cos60°2sin45°
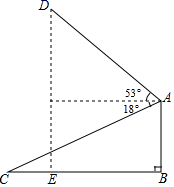
如图,某工地有一辆吊车,  为车身,
为车身,  为吊臂,吊车从水平地面C处吊起货物,此时测得吊臂
为吊臂,吊车从水平地面C处吊起货物,此时测得吊臂  与水平线的夹角为
与水平线的夹角为  .当货物吊至D处时,测得吊臂
.当货物吊至D处时,测得吊臂  与水平线的夹角为
与水平线的夹角为 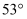 ,且吊臂转动过程中长度始终保持不变,此时D处离水平地面的高度
,且吊臂转动过程中长度始终保持不变,此时D处离水平地面的高度 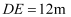 ,求吊臂的长.(结果保留一位小数,参考数据:
,求吊臂的长.(结果保留一位小数,参考数据: 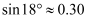 ,
, 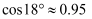 ,
,  ,
, 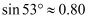 ,
,  ,
,  )
)
 为车身,
为车身,  为吊臂,吊车从水平地面C处吊起货物,此时测得吊臂
为吊臂,吊车从水平地面C处吊起货物,此时测得吊臂  与水平线的夹角为
与水平线的夹角为  .当货物吊至D处时,测得吊臂
.当货物吊至D处时,测得吊臂  与水平线的夹角为
与水平线的夹角为 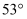 ,且吊臂转动过程中长度始终保持不变,此时D处离水平地面的高度
,且吊臂转动过程中长度始终保持不变,此时D处离水平地面的高度 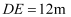 ,求吊臂的长.(结果保留一位小数,参考数据:
,求吊臂的长.(结果保留一位小数,参考数据: 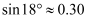 ,
, 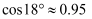 ,
,  ,
, 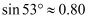 ,
,  ,
,  )
) 
计算:  .
.
 .
.
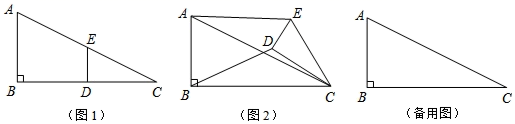
如图1,在  中,∠B=90°,
中,∠B=90°, 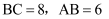 ,点D,E分别是边BC,AC的中点,连接
,点D,E分别是边BC,AC的中点,连接 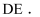 将
将  绕点C按顺时针方向旋转,记旋转角为
绕点C按顺时针方向旋转,记旋转角为  .
.
 中,∠B=90°,
中,∠B=90°, 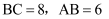 ,点D,E分别是边BC,AC的中点,连接
,点D,E分别是边BC,AC的中点,连接 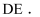 将
将  绕点C按顺时针方向旋转,记旋转角为
绕点C按顺时针方向旋转,记旋转角为  .
. 
-
(1) 问题发现:
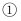 当
当  时,
时,  ;
;  当
当 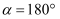 时,
时,  .
. -
(2) 拓展探究:
试判断:当
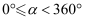 时,
时, 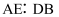 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明. -
(3) 问题解决:
当
 旋转至A、D、E三点共线时,直接写出线段BD的长.
旋转至A、D、E三点共线时,直接写出线段BD的长.
已知反比例函数的图象经过点(m,6)和(﹣2,3),则m的值为.
在比例尺为  的工程图上,南京地铁四号线全长约
的工程图上,南京地铁四号线全长约  ,它的实际长度约为
,它的实际长度约为 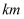
 的工程图上,南京地铁四号线全长约
的工程图上,南京地铁四号线全长约  ,它的实际长度约为
,它的实际长度约为 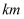
反比例函数 的图象在( )
的图象在( )
 的图象在( )
的图象在( )
A . 第一、三象限
B . 第二、四象限
C . 第一、二象限
D . 第一、四象限
2020年是紫禁城建成600年暨故宫博物院成立95周年,在此之前有多个国家曾发行过紫禁城元素的邮品.图1所示的摩纳哥发行的小型张中的图案,以敞开的紫禁城大门和大门内的石狮和太和殿作为邮票和小型张的边饰.如果标记出图1中大门的门框并画出相关的几何图形(图2),我们发现设计师巧妙地使用了数学元素(忽略误差),图2中的四边形  与四边形
与四边形 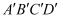 是位似图形,点
是位似图形,点  是位似中心,点
是位似中心,点 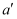 是线段
是线段  的中点,那么以下结论正确的是( )
的中点,那么以下结论正确的是( )
 与四边形
与四边形 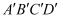 是位似图形,点
是位似图形,点  是位似中心,点
是位似中心,点 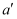 是线段
是线段  的中点,那么以下结论正确的是( )
的中点,那么以下结论正确的是( ) 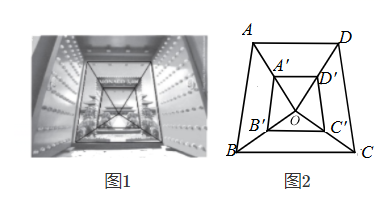
A . 四边形  与四边形
与四边形 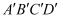 的相似比为1:1
B . 四边形
的相似比为1:1
B . 四边形  与四边形
与四边形 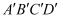 的相似比为1:2
C . 四边形
的相似比为1:2
C . 四边形  与四边形
与四边形 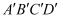 的相似比为3:1
D . 四边形
的相似比为3:1
D . 四边形  与四边形
与四边形 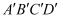 的面积比为4:1
的面积比为4:1
 与四边形
与四边形 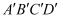 的相似比为1:1
B . 四边形
的相似比为1:1
B . 四边形  与四边形
与四边形 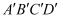 的相似比为1:2
C . 四边形
的相似比为1:2
C . 四边形  与四边形
与四边形 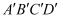 的相似比为3:1
D . 四边形
的相似比为3:1
D . 四边形  与四边形
与四边形 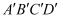 的面积比为4:1
的面积比为4:1
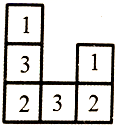
如图,是一个由小正方体所搭成的几何体,从上面看到的平面图形,从正方形中的数字表示该位置小正方体的个数,请你画出它从正面和从左面看到的平面图形.
一个圆锥的底面半径  ,高
,高  ,则这个圆锥的侧面积是(结果取整数).
,则这个圆锥的侧面积是(结果取整数).
 ,高
,高  ,则这个圆锥的侧面积是(结果取整数).
,则这个圆锥的侧面积是(结果取整数).
郑在一次拼图游戏中,发现了一个很神奇的现象:
⑴他先用图形①②③④拼出矩形ABCD.
⑵接着拿出图形⑤ .
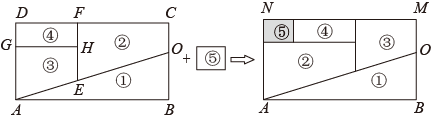
⑶通过平移的方法,用①②③④⑤拼出了矩形ABMN.已知AE:EO = 2:3,图形④的面积为15,则增加的图形⑤的面积为:,当CO= , EH=4时,tan∠BAO=.
, EH=4时,tan∠BAO=.
⑴他先用图形①②③④拼出矩形ABCD.
⑵接着拿出图形⑤ .
⑶通过平移的方法,用①②③④⑤拼出了矩形ABMN.已知AE:EO = 2:3,图形④的面积为15,则增加的图形⑤的面积为:,当CO=
 , EH=4时,tan∠BAO=.
, EH=4时,tan∠BAO=.
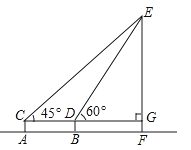
如图,为了测得铁塔的高度,小莹利用自制的测角仪,在C点测得塔顶E的仰角为45°,在D点测得塔顶E的仰角为60°,已知测角仪AC的高为1.6米,CD的长为6米,CD所在的水平线CG⊥EF于点G,铁塔EF的高为米.(结果用带根号的式子表示)
最近更新
- 23请用100字左右叙述相关的情节(任选一题) (1)《子夜》中吴荪甫对工人罢工残酷镇压的故事。 (2)恩格斯指
- For most of the day construction worker Sidney Smith and his
- 下列各式中计算结果是的是()A.B.C.D.
- 全球经济下行压力之下。中小企业发展愈加困难。为此,我国进一步加大结构性减税力度,拓宽减税范围。为中小企业减负,促进其转型
- 如图所示是课本中的几个实验.演示磁场对通电导体有力的作用的是() A. B. C. D.
- 下列哪项不属于生物防治( ) A.以农药治虫; B.以虫治虫; C.以鸟治虫;D.以菌治虫。
- 函数满足时,,求此函数的单调区间。
- 下列词语中加点的字,读音完全相同的一项是 ( ) A.遨游
- 如图是甲、乙两种固体的溶解度曲线,下列说法错误的是()A.10℃时,等质量的甲和乙的饱和溶液中溶质质量相等 B.30℃时
- 2012年8月6日,美国“好奇”号火星车成功登陆火星表面,随后传送回火星表面比较清晰的照片。下面是有关火星与地球的比较数
- 下列历史事件,把世界连成一个整体,并促进了资本主义的产生和发展的是 A.资产阶级革命 B.郑和下西洋 C
- 2.下列选项中加横线字的解释不正确的一项是 A.天下莫不与也 与:亲附。 B.骄其妻妾
- 下列物质中由于发生化学反应而能使溴水褪色,又能使KMnO4酸性溶液褪色的是( )A.SO2
- 分式方程的解是…………………………………(▲)A.B.C.D.或
- They promise that the work would all be finished _____ next
- 右图表示某些物质间转化关系。其中A、E、G为固体,且A、G均为单质,E为红棕色固体,G为常见金属; C、F、D、H为无色
- 下表是四地一年中昼长最大差值(R)和正午太阳高度最大差值(H)资料。据此回答问题。① ② ③ ④ R 2小时26分 24
- At home, ordering food from a menu is anormal, everyday rout
- 李贺《李凭箜篌引》中直接摹写乐声激越动听的诗句是:“_______________,_______________。”
- 下图一、二、三是酶促反应的相关曲线,已知图一是H2O2酶催化H2O2实验,曲线1是在土豆片为4 温度为35 ℃的条件下测



