九年级(初三)数学下学期下册试题
下列几何体中从正面、左面和上面看到的图形完全相同的是( )
A . 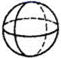 B .
B .  C .
C . 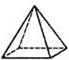 D .
D . 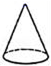
 B .
B .  D .
D . 
已知k1<0<k2 , 则函数 和
和 的图象大致是( )
的图象大致是( )
 和
和 的图象大致是( )
的图象大致是( )
A . 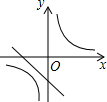 B .
B . 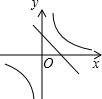 C .
C . 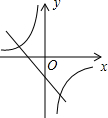 D .
D . 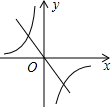
 B .
B .  C .
C .  D .
D . 
在△ABC中,∠C=90°,BC=3,AB=5,则sinA的值是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
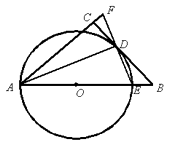
如图,在△ABC中,∠ACB=90°,O是AB上一点,以OA为半径的⊙O与BC相交于点D,与AB交于点E,AD平分∠FAB,连接ED并延长交AC的延长线于点F.
-
(1) 求证:BC为⊙O的切线.
-
(2) 求证:AE=AF;
-
(3) 若DE=3,sin∠BDE=
 ,求AC的长.
,求AC的长.
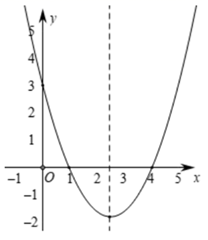
如图,抛物线y=ax2+bx+3经过A (1,0)、B(4,0)两点,与y轴交于点C.
-
(1) 求该抛物线的解析式;
-
(2) 如图,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;不存在,请说明理由.
-
(3) 在(2)的条件下,点Q是线段OB上一动点,当△BPQ与△BAC相似时,求点Q的坐标.
已知一块蓄电池的电压为定值,以此蓄电池为电源时,电流I(A)与电阻R(Ω)之间的函数关系如图,则电流I关于电阻R的函数解析式为( )
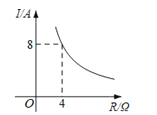
A . I=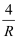 B . I=
B . I=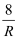 C . I=
C . I=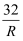 D . I=-
D . I=-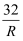
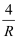 B . I=
B . I=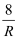 C . I=
C . I=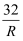 D . I=-
D . I=-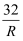
反比例函数 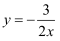 的比例系数是.
的比例系数是.
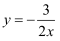 的比例系数是.
的比例系数是.
下列各式正确的是( )
A . cos60°<sin45°<tan45°
B . sin45°<cos60°<tan45°
C . sin45°<tan45°<cos60
D . cos60°<tan45°<sin45°
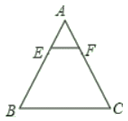
如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.
(1)求EC的值;
(2)求证:AD•AG=AF•AB.

已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.
-
(1) k的值是;
-
(2) 如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数y=
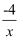 图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若
图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若 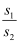 =
= 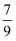 ,则b的值是.
,则b的值是. 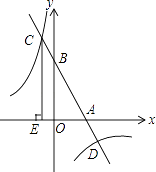
在抗击“新冠病毒”期间,某路口利用探测仪对过往的物体进行检查,探测仪A测得某物体的仰角∠BAD  30°,俯角∠DAC
30°,俯角∠DAC  45°,探测仪到货物表面的距离AD
45°,探测仪到货物表面的距离AD  3米,求货物高BC的长.(
3米,求货物高BC的长.(  ≈1.73,结果精确到0.1)
≈1.73,结果精确到0.1)
 30°,俯角∠DAC
30°,俯角∠DAC  45°,探测仪到货物表面的距离AD
45°,探测仪到货物表面的距离AD  3米,求货物高BC的长.(
3米,求货物高BC的长.(  ≈1.73,结果精确到0.1)
≈1.73,结果精确到0.1) 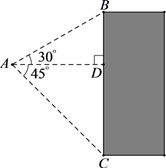
已知,如图Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,点P为AC的中点,Q从点A运动到B,点Q运动到点B停止,连接PQ,取PQ的中点O,连接OC,OB.

-
(1) 若△ABC∽△APQ,求BQ的长;
-
(2) 在整个运动过程中,点O的运动路径长;
-
(3) 以O为圆心,OQ长为半径作⊙O,当⊙O与AB相切时,求△COB的面积.
已知圆锥的母线长为6cm,侧面积为12πcm2 , 那么它的底面圆半径为 cm.
如图,在  中,
中,  ,则
,则  四边形
四边形  =( )
=( )
 中,
中,  ,则
,则  四边形
四边形  =( )
=( )
A . 7
B . 8
C . 9
D . 10
在某次海上军事学习期间,我军为确保△OBC海域内的安全,特派遣三艘军舰分别在O、B、C处监控△OBC海域,在雷达显示图上,军舰B在军舰O的正东方向80海里处,军舰C在军舰B的正北方向60海里处,三艘军舰上装载有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域.(只考虑在海平面上的探测)

-
(1) 若三艘军舰要对△OBC海域进行无盲点监控,则雷达的有效探测半径r至少为多少海里?
-
(2) 现有一艘敌舰A从东部接近△OBC海域,在某一时刻军舰B测得A位于北偏东60°方向上,同时军舰C测得A位于南偏东30°方向上,求此时敌舰A离△OBC海域的最短距离为多少海里?
-
(3) 若敌舰A沿最短距离的路线以20
 海里/小时的速度靠近△OBC海域,我军军舰B沿北偏东15°的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?
海里/小时的速度靠近△OBC海域,我军军舰B沿北偏东15°的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?
如图是一正方体展开图,则有、志、者三面的对面分别是( )
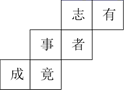
A . 事竟成
B . 事成竟
C . 成竟事
D . 竟成事
△ABC∽△DEF且它们的面积比为 , 则周长比是( )
, 则周长比是( )
 , 则周长比是( )
, 则周长比是( )
A . 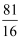 B .
B .  C .
C .  D .
D . 
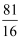 B .
B .  C .
C .  D .
D . 
计算:

图1所示的是一个上下两个面都为正方形的长方体,现将图1的一个角切掉,得到图2所示的几何体,则图2的俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在梯形  中,
中,  ,
, 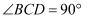 ,
,  ,对角线
,对角线  和
和  相交于点
相交于点  ,等腰直角
,等腰直角  的直角顶点
的直角顶点  与梯形的顶点
与梯形的顶点  重合,将
重合,将  绕点
绕点  旋转
旋转
 中,
中,  ,
, 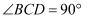 ,
,  ,对角线
,对角线  和
和  相交于点
相交于点  ,等腰直角
,等腰直角  的直角顶点
的直角顶点  与梯形的顶点
与梯形的顶点  重合,将
重合,将  绕点
绕点  旋转
旋转 
-
(1) 如图1,当
 的一边
的一边 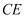 落在
落在  边上,另一边
边上,另一边 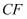 落在
落在 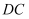 边的延长线上时,求证:
边的延长线上时,求证: 
-
(2) 继续旋转
 ,旋转角为
,旋转角为  ,请你在图2中画出图形,并判断(1)中的结论是否成立?若成立加以证明:若不成立,说明理由;
,请你在图2中画出图形,并判断(1)中的结论是否成立?若成立加以证明:若不成立,说明理由;
-
(3) 如图3,继续旋转
 ,当三角形的一边
,当三角形的一边 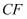 与梯形对角线
与梯形对角线  重合,
重合,  与
与  相交于点
相交于点  时,若
时,若 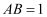 ,
,  ,
, 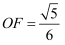 ,分别求出线段
,分别求出线段  、
、  、
、  的长.
的长.
最近更新
- 方程2x+3x-7=0的近似解(精确到0.1)是x=__________.
- 假定去年某国待售商品价格总额为2000亿元,货币流通次数为4次。今年该国待售商品价格总额增加了10%,而实际纸币发行量为
- 生物分类单位由小到大是:界、门、纲、目、科、属、种。 ( )
- 从学校乘汽车到火车站的途中有3个交通岗,假设在各个交通岗遇到红灯的事件是相互独立的,并且概率都是,设ξ为途中遇到红灯的次
- 随着科技的发展,人们有可能通过操纵单个原子来制造分子,若用这种方法制造葡萄糖[C6H12O6],则不需要的原子是 A、碳
- Ⅰ.用纯净的碳酸钙与稀盐酸反应制取二氧化碳气体,请回答:(1)实验过程如图所示,分析判断:段化学反应速率最快,段收集的二
- 阅读下面短文,根据文章内容,将文中划线句子(1—2小题)翻译成汉语,并回答3~5小题所提问题。 (1)In northe
- 二)古代诗歌阅读(10分) 阅读下面一首唐诗,完成14~15题。 晚次湖口有怀(节选) 刘长卿 帝乡劳想望,万里心来去。
- 下列各组转化关系中的反应为初中化学常见的反应,其中的“→”表示某种物质可一步反应生成另一种物质。甲、乙、丙三种物质不符合
- 在地球五带中,北温带与热带的分界线是 ( ) A、南回归线 B、北
- 下列各项中,没有语病的一项是 A.首赴亚丁湾、索马里海域执行护航任务的中国海军的三艘军舰和几十名特种兵,将进行登舰检查、
- 读我国甘蔗、甜菜和某种工业产品生产厂分布图(图7),回答16~17题。 16.造成甘蔗、甜菜产区空间分布差异的主要因素
- 赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上
- (10分)830K时,在密闭容器中发生下列可逆反应:CO(g)+H2O(g)CO2(g)+H2(g) △H<0 试回
- 下列反应中,既不是化合反应,又不是分解反应的是 A.铁丝在氧气中燃烧
- 将紫色萝卜的块根切成小块放入清水中,水的颜色无明显变化。若对其进行加温,随着水温的升高,水的颜色会逐渐变红。其原因是(
- 物质的性质决定物质的用途.按要求从氧气、氢气、盐酸、氯化钠、浓硫酸、水、氢氧化钠中选择合适的物质,将其化学式填写在下列空
- Things of_____ kind come together;people of ____kind fall in
- (2006·湖南益阳中考)在一个枝芽中,位于幼叶叶腋里的突起是( )。A.叶原基B.芽原基C.生长点D.芽轴
- 补出下列名句名篇的空缺部分 (1)谁言寸草心, 。



