九年级(初三)数学下学期下册试题
如图,在△ABC中,DE∥AB,且 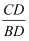 =
=  ,则
,则 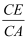 的值为( )
的值为( )
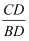 =
=  ,则
,则 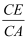 的值为( )
的值为( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
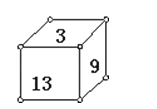
如图,立方体的每一个面上都有一个自然数,已知相对的两个面上二数之和相等.如果13,9,3的对面的数分别是a,b,c,试求a2+b2+c2﹣ab﹣bc﹣ca之值.
如图是由几个相同的小正方体分别从上面、左面看到的形状图,这样的几何体最多需要个小立方体块,最少需要个小立方体块.
如图,平面直角坐标系xOy中,点A、B的坐标分别为(9,0)、(6,﹣9),△AB'O'是△ABO关于点A的位似图形,且O'的坐标为(﹣3,0),则点B'的坐标为( )

A . (8,﹣12)
B . (﹣8,12)
C . (8,﹣12)或(﹣8,12)
D . (5,﹣12)
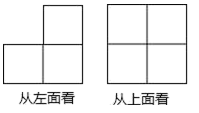
如图,是由若干个相同的小立方体搭成的几何体的俯视图和左视图.则小立方体的个数可能是( )

A . 5或6
B . 5或7
C . 4或5或6
D . 5或6或7
构建几何图形解决代数问题是“数形结合”思想的重要性,在计算  时,如图.在
时,如图.在  中,
中,  ,
,  ,延长
,延长 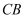 使
使  ,连接
,连接  ,得
,得 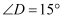 ,所以
,所以  .类比这种方法,计算
.类比这种方法,计算  的值为.
的值为.
 时,如图.在
时,如图.在  中,
中,  ,
,  ,延长
,延长 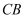 使
使  ,连接
,连接  ,得
,得 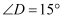 ,所以
,所以  .类比这种方法,计算
.类比这种方法,计算  的值为.
的值为. 
如图,已知 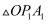 、
、  、
、  、…均为等腰直角三角形,直角顶点
、…均为等腰直角三角形,直角顶点  、
、  、
、  、…在函数
、…在函数 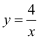
 图象上,点
图象上,点  、
、  、
、  、
、  在
在  轴的正半轴上,则点
轴的正半轴上,则点  的横坐标为.
的横坐标为.
 、
、  、
、  、…均为等腰直角三角形,直角顶点
、…均为等腰直角三角形,直角顶点  、
、  、
、  、…在函数
、…在函数 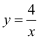
 图象上,点
图象上,点  、
、  、
、  、
、  在
在  轴的正半轴上,则点
轴的正半轴上,则点  的横坐标为.
的横坐标为. 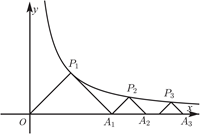
如图,在A点有一个热气球,由于受西风的影响,以20米/分的速度沿与地面成 角的方向飞行,10分钟后到达C处,此时热气球上的人测得地面上的B点俯角为
角的方向飞行,10分钟后到达C处,此时热气球上的人测得地面上的B点俯角为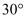 , 则A、B两点间的距离为米.
, 则A、B两点间的距离为米.
 角的方向飞行,10分钟后到达C处,此时热气球上的人测得地面上的B点俯角为
角的方向飞行,10分钟后到达C处,此时热气球上的人测得地面上的B点俯角为 , 则A、B两点间的距离为米.
, 则A、B两点间的距离为米.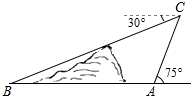
已知,如图,直线AB经过点B(0,6),且tan∠ABO=  ,与抛物线y=ax2+2在第一象限内相交于点P,又知△AOP的面积为6.
,与抛物线y=ax2+2在第一象限内相交于点P,又知△AOP的面积为6.
 ,与抛物线y=ax2+2在第一象限内相交于点P,又知△AOP的面积为6.
,与抛物线y=ax2+2在第一象限内相交于点P,又知△AOP的面积为6. 
-
(1) 求a的值;
-
(2) 能否将抛物线y=ax2+2平移使得平移后的抛物线经过点A?
对于双曲线y=  ,当x>0时,y随x的增大而减小,则m的取值范围为( )
,当x>0时,y随x的增大而减小,则m的取值范围为( )
 ,当x>0时,y随x的增大而减小,则m的取值范围为( )
,当x>0时,y随x的增大而减小,则m的取值范围为( )
A . m>0
B . m>1
C . m<0
D . m<1
如图,身高是1.6m的某同学直立于旗杆影子的顶端处,测得同一时刻该项同学和旗杆的影子长分别为1.2m和9m,则旗杆的高度为 m.

在△ABC中,∠B、∠C 均为锐角,其对边分别为b、c,求证:

在平面直角坐标系中,抛物线L:y=﹣x2+x+2与y轴交于点C,与x轴交于A、B两点(点A在点B的左侧).

-
(1) 求A、B、C三点的坐标;
-
(2) 连接AC、BC,以点C为位似中心,将△ABC扩大到原来的2倍得到△A1B1C,其中点A1、B1分别是点A、B的对应点,如何平移抛物线L才能使其同时经过点A1、B1 , 求出所有的平移方式.
某斜坡的坡度 , 则该斜坡的坡角为.
, 则该斜坡的坡角为.
 , 则该斜坡的坡角为.
, 则该斜坡的坡角为.
如图,O为坐标原点,点C的坐标为(1,0),∠ACB=90°,∠B=30°,当点A在反比例函数y=  的图象上运动时,点B在函数(填函数解析式)的图象上运动.
的图象上运动时,点B在函数(填函数解析式)的图象上运动.
 的图象上运动时,点B在函数(填函数解析式)的图象上运动.
的图象上运动时,点B在函数(填函数解析式)的图象上运动. 
已知点(x1 ,-1),(x2 ,  ),(x3 ,3)都在反比例函数
),(x3 ,3)都在反比例函数  的图象上,则x1 ,x2,x3的大小关系是( )
的图象上,则x1 ,x2,x3的大小关系是( )
 ),(x3 ,3)都在反比例函数
),(x3 ,3)都在反比例函数  的图象上,则x1 ,x2,x3的大小关系是( )
的图象上,则x1 ,x2,x3的大小关系是( )
A . x1> x2>x3
B . x1>x3>x2
C . x2>x1 >x3
D . x3 >x1>x2
某一时刻,树AB在阳光下的影子一部分在地面上,另一部分在建筑物的墙面上.设树AB在地面上的影长BC为5.2m,墙面上的影长CD为1.5m;同一时刻测得竖立于地面长1m的木杆的影长为0.8m,求树高.

一个几何体的三视图如图所示(单位:mm),你能画出这个几何体的图形吗?并求出其表面积和体积.

如图, 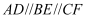 ,直线
,直线  ,
,  与这三条平行线分别交于点
与这三条平行线分别交于点  ,
,  ,
,  和点
和点  ,
,  ,
,  ,已知
,已知 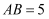 ,
,  ,
, 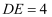 ,则
,则  的长为?
的长为?
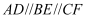 ,直线
,直线  ,
,  与这三条平行线分别交于点
与这三条平行线分别交于点  ,
,  ,
,  和点
和点  ,
,  ,
,  ,已知
,已知 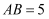 ,
,  ,
, 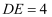 ,则
,则  的长为?
的长为? 
已知 <cosA<sin80°,则锐角A的取值范围是( )
<cosA<sin80°,则锐角A的取值范围是( )
 <cosA<sin80°,则锐角A的取值范围是( )
<cosA<sin80°,则锐角A的取值范围是( )
A . 60°<A<80°
B . 30°<A<80°
C . 10°<A<60°
D . 10°<A<30°
最近更新
- 当今时代,“被”字句广为流行,“被自杀”、“被统计”、“被就业”、“被小康”、“被代表”、“被自愿”......“被时代
- 设函数f(x)=2在处取最小值. (1) 求.的值; (2) 在ABC中,分别是角A,B,C的对边,已知,求角
- 细胞膜上与细胞的识别、免疫反应、信息传递和血型决定有密切关系的化学物质是 A.糖蛋白 B.磷脂 C.脂肪
- 下列各组物质中,能相互反应且反应前后溶液总质量保持不变的是() A.铝和硫酸铜溶液 B.稀硫酸和烧碱
- 医院里检验病人患某种疾病的方法是将病人的尿液滴加在硫酸铜和氢氧化钠的混合液中,加热后有红色沉淀生成,说明病人尿液里含(
- —Why haven’t you brought my English dictionaryback? —I______
- 二战后,拉丁美洲和加勒比地区曾是全世界城镇化速度最快的地区。过度的城镇化进程使城镇人口数量大大超过工业化所能吸纳的程度,
- 用焦距10cm的凸透镜做“探究凸透镜成像规律”的实验,如题17图所示。(凸透镜的位置固定不动) ⑴为了便于观察实验现
- 在钠的焰色反应实验中,不需要的仪器或药品是A、铂丝棒 B.酒精灯 C.蓝色钴玻璃 D.稀盐酸
- “路漫漫其修远兮,吾将上下而求索”、“行路难,行路难,多歧路,今安在”、“没有比人更高的山,没有比脚更长的路”、“走自己
- (13分)请认真阅读下列三个反应:利用这些反应,按以下步骤可从某烃A合成一种染料中间体DSD酸:请写出A、B、C、D的结
- 美国国务卿马歇尔曾提出的“欧洲复兴计划”宣称:“我们的政策的目的是恢复世界上行 之有效的经济制度,从而使自由制度赖以存在
- 在△ABC中,已知AB=,AC边上的中线BD=,求sinA的值.
- 氢化钙(CaH2)固体可用于登山队员的能源提供剂,与氢气做能源相比它的优点是
- Daredevil climber Alain Robert, known as the French Spiderma
- 读表,回答8-9题。 8. 表中①②③④所对应的地区分别是( ) A. 东南、西南、华北、西北
- 10.对下面的这首唐诗理解不正确的一项是( )(2分) 凉州词 王之涣 黄河远上白云间,一片
- 若=1,则cos2θ的值为………………………………( )(A)
- 已知口袋中有大小相同的m个红球和n个白球,m≥n≥2,从袋中任意取出两个球.(1)若m=4,n=3,求取出的两个球中至少
- 运用溶解度表与溶解度曲线回答下列问题:(1)氯化钠的溶解度曲线是 (填“A”或“B”)。 (2)60



