九年级(初三)数学下学期下册试题
若一个几何体的三种视图如图所示,则该几何体是( )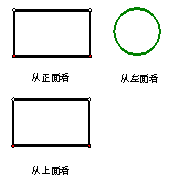
A . 正方体
B . 圆柱体
C . 圆锥体
D . 球体
如图是某几何体的三视图,该几何体是( )
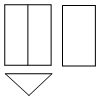
A . 三棱柱
B . 三棱锥
C . 圆柱
D . 圆锥
已知:如图,是一几何体的三视图,则该几何体的名称为( )
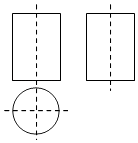
A . 长方体
B . 正三棱柱
C . 圆锥
D . 圆柱
下列说法对吗?
(1)分别在△ABC的边AB,AC上取点D,E,使DE∥BC,那么△ADE是△ABC缩小后的图形.
(2)分别在△ABC的边AB,AC的延长线上取点D,E,使DE∥BC,那么△ADE是△ABC放大后的图形.
(3)分别在△ABC的边AB,AC的反向延长线上取D,E,使DE∥BC,那么△ADE是△ABC放大后的图形.
已知圆柱的侧面积是10πcm2 , 若圆柱底面半径为rcm,高为hcm,则h与r的函数关系式是
在Rt△ABC中,∠ACB=90°,点D在边AC上,DE⊥B于点E,连CE.
-
(1)
如图1,已知AC=BC,AD=2CD,

①△ADE与△ABC面积之比;
②求tan∠ECB的值;
-
(2)
如图2,已知
 =
=  =k,求tan∠ECB的值(用含k的代数式表示).
=k,求tan∠ECB的值(用含k的代数式表示).
如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,CD⊥AB于D,设∠ACD=α,则cosα的值为( )
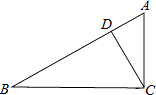
A . 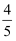 B .
B . 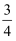 C .
C . 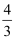 D .
D . 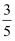
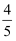 B .
B . 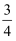 C .
C . 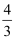 D .
D . 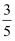
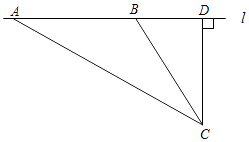
某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于24米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.
-
(1) 求AB的长(结果保留根号);
-
(2) 已知本路段对校车限速为45千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.
如图,小明在A时测得某树的影长为  ,B时又测得该树的影长为
,B时又测得该树的影长为  ,若两次日照的光线互相垂直,则树的高度为m.
,若两次日照的光线互相垂直,则树的高度为m.
 ,B时又测得该树的影长为
,B时又测得该树的影长为  ,若两次日照的光线互相垂直,则树的高度为m.
,若两次日照的光线互相垂直,则树的高度为m. 
在某一时刻,操场上有三根测杆,如图所示,其中测杆AB的影子为BC,你能画出测杆MN的影子NP吗?若测杆XY的影子的顶端恰好落在点B处,且XY=MN,你能找出XY所在的位置吗?请将上述问题画在下面的示意图中,并简述画法.

如图1,等腰△ABC中,AC=BC,点O在AB边上,以O为圆心的圆经过点C,交AB边于点D,EF为⊙O的直径,EF⊥BC于点G,且D是  的中点.
的中点.
 的中点.
的中点. 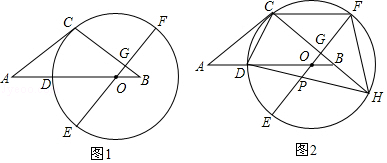
-
(1) 求证:AC是⊙O的切线;
-
(2) 如图2,延长CB交⊙O于点H,连接HD交OE于点P,连接CF,求证:CF=DO+OP;
-
(3) 在(2)的条件下,连接CD,若tan∠HDC=
 ,CG=4,求OP的长.
,CG=4,求OP的长.
小虎同学在计算a+2cos60°时,因为粗心把“+”看成“﹣”,结果得2006,那么计算a+2cos60°的正确结果应为
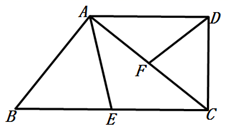
已知:如图,直角梯形  中,
中,  ,点E在边
,点E在边  上,点F在对角线
上,点F在对角线  上,且
上,且  .
.
 中,
中,  ,点E在边
,点E在边  上,点F在对角线
上,点F在对角线  上,且
上,且  .
. 
-
(1) 求证:
 ;
;
-
(2) 当点E、F分别是边
 的中点时,求证:
的中点时,求证:  .
.
如图①,是一个每条棱长均相等的三棱锥,图②是它的主视图、左视图与俯视图.若边AB的长度为a,则在这三种视图的所有线段中,长度为a的线段条数是( )

A . 12条
B . 9条
C . 6条
D . 5条
如图,反比例函数y1= 的图象与正比例函数y2=k2x的图象交于点(2,1),则使y1>y2的x的取值范围是( )
的图象与正比例函数y2=k2x的图象交于点(2,1),则使y1>y2的x的取值范围是( )

A . 0<x<2
B . x>2
C . x>2或-2<x<0
D . x<-2或0<x<2
如图,在矩形ABCD中,以点A为圆心,AD的长为半径画弧,交AB于点E,取BC的中点F,过点F作一直线与AB平行,且交弧DE于点G,则∠AGF的度数为 ( )
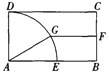

A . 110°
B . 120°
C . 135°
D . 150°
我们知道良好的坐姿有利于青少年骨骼生长,有利于身体健康,那么首先要有正确的写字坐姿,身子上半部坐直,头部端正、目视前方,两手放在桌面上,两腿平放,胸膛挺起,理想状态下,如图1所示,将图1中的眼睛记为点A,腹记为点B,笔尖记为点D,且BD与桌沿的交点记为点C
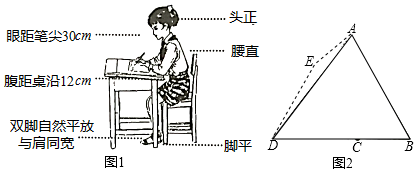
参考数据:sin53°≈0.80,cos53°≈0.60,.tan53°≈1.33, ≈1.41,
≈1.41, ≈1.73)
≈1.73)
-
(1) 若∠ADB=53°,∠B=60°,求A到BD的距离及C、D两点间的距离(结果精确到1cm).
-
(2) 老师发现小红同学写字姿势不正确,眼睛倾斜至图2的点E,点E正好在CD的垂直平分线上,且∠BDE=60°,于是要求其纠正为正确的姿势.求眼睛所在的位置应上升的距离.(结果精确到1cm)
如图,该几何体的主视图是( )
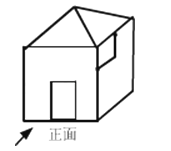
A . 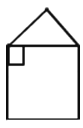 B .
B . 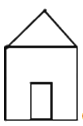 C .
C . 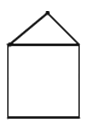 D .
D . 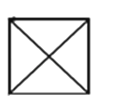
 B .
B .  C .
C .  D .
D . 
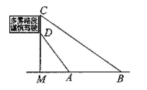
如图,是矗立在高速公路水平地面上的交通牌,经测量得到如下数据: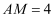 米,
米,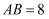 米,
米,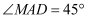 ,
, 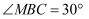 , 则警示牌的高CD为米.(结果精确到0.1.参考数据:
, 则警示牌的高CD为米.(结果精确到0.1.参考数据: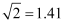 ,
, 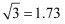 )
)
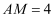 米,
米,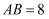 米,
米,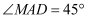 ,
, 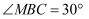 , 则警示牌的高CD为米.(结果精确到0.1.参考数据:
, 则警示牌的高CD为米.(结果精确到0.1.参考数据: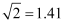 ,
, 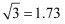 )
) 
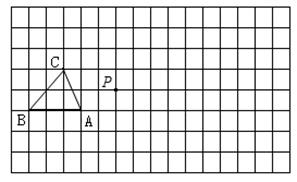
在下面的正方形网格中,每个小正方形的边长为1个单位,△ABC是格点三角形(顶点在网格交点处),请你画出:
-
(1) △ABC的中心对称图形△A1B1C1 , A点为对称中心;
-
(2) △ABC关于点P的位似△A'B'C',且位似比为1:2;
-
(3) 找出以A、B、C、D为顶点的所有格点平行四边形ABCD的顶点D。
最近更新
- 关于药品的取用有下列说法不正确的是( ) ①实验中剩余的药品要放回原试剂瓶,以免浪费②实验中剩余的药品随手扔掉
- 如图表示人小肠结构中的两种细胞。关于这两种细胞的叙述,不正确的是()A.所含遗传信息相同 B.所含蛋白质种类相同 C.细
- 吞咽食物和呼吸空气时都经过的器官是 ( ) A.咽
- 已知向量 =(1,1),向量与向量的夹角为,且. (1)求向量; (2)设向量=(1,0),向量=(cosx,2cos2
- (1) ,秋水共长天一色。(王勃《滕王阁序》)(2)惟有绿荷红菡萏, 。(李
- 物理知识在平时的生产、生活中有着广泛的应用,下列说法中正确的是( ) A.鞋底刻有不同的花纹,主要是为了增大鞋底
- 假如在某一年里,全社会用现金支付的销售商品总量为5 000亿件,平均每件价格水平为8元,在这一年里货币平均周转5次。那么
- .中华民国南京临时政府成立时实行总统制,《临时约法》改总统制为责任内阁制,袁世凯正式就任大总统后,又改责任内阁制为总统制
- 在集气瓶内使O2和CH4混合,点燃进行爆炸性实验,下列CH4与O2体积比(同温、同压)中使爆炸响声最大的是( )
- 一个物体位移与时间的关系为s=5t+5t2(s以m为单位,t以s为单位),下列说法中正确的是( ) A.这个物体的
- (16分)某实验小组用下列装置进行乙醇催化氧化的实验。⑴实验过程中铜网出现红色和黑色交替的现象,请写出相应的化学方程式
- 按要求作文。 生活中,许多人和事的意义不是单一的。比如,成长,不只是年龄的增长,更是心智的成熟;出发,不只是为了
- 假定英语课上老师要求同桌之间交换修改作文,请你修改你同桌写的以下作文。文中共有10处语言错误,每句中最多有两处。每处错误
- 下列各组划线字解释中有错误的一项是(2分)( ) A.普明日复奏其人(第二天) B.我以日始出时去人近(离开) C.
- 短周期元素X、Y可以形成化合物XY2,下列有关叙述不正确的是( )A.若XY2是共价化合物,则X与Y的原子序数可能相
- 若展开式的二项式系数之和为64,则展开式的常数项为 ( ) A.10 B.
- Frank lives a simple life______ he has lots of money. A. a
- 读我国夏季平均气温图(图6-5),完成下列要求: (1)下列地区中,气温最低且原因表述正确的是 (单项
- 海洋水体运动的主要动力是() A.大气运动和近地面风带 B.地球自转偏向力 C.海水密
- 有关世界各地牧场退化情况,叙述不正确的是A. 欧洲情况较好,载畜量最高 B. 北美和澳大利亚情况最好C.



