九年级(初三)数学下学期下册试题
下列几何体中,侧面展开图是矩形的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )

A . 288°
B . 144°
C . 216°
D . 120°
如图,是一个正方体的展开图,若在其中的三个正方形  、
、  、
、  内分别填入适当的数,使得折叠成正方体后,相对面上的两个数互为相反数,则填入正方形中
内分别填入适当的数,使得折叠成正方体后,相对面上的两个数互为相反数,则填入正方形中  、
、  、
、  内的三个数依次是( )
内的三个数依次是( )
 、
、  、
、  内分别填入适当的数,使得折叠成正方体后,相对面上的两个数互为相反数,则填入正方形中
内分别填入适当的数,使得折叠成正方体后,相对面上的两个数互为相反数,则填入正方形中  、
、  、
、  内的三个数依次是( )
内的三个数依次是( ) 
A . 0,-1,2
B . 0,2,-1
C . 2,-1,0
D . -1,0,2
如图

-
(1) 如图,锐角的正弦和余弦都随着锐角的确定而确定,也随着其变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值的变化规律;
-
(2) 根据你探索到的规律,试比较18°,34°,52°,65°,88°,这些角的正弦值的大小和余弦值的大小;
-
(3) 比较大小:(在空格处填写“<”或“>”或“=”)
若∠α=45°,则sinαcosα;若∠α<45°,则sinαcosα;若∠α>45°,则sinαcosα;
-
(4) 利用互余的两个角的正弦和余弦的关系,比较下列正弦值和余弦值的大小:
sin10°,cos30°,sin50°,cos70°.
圆锥的母线长为6cm,底面圆半径为2cm,则圆锥的侧面积为.
如图, 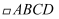 的顶点A , C在反比例函数
的顶点A , C在反比例函数 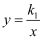 的图象上,顶点B , D在反比例函数
的图象上,顶点B , D在反比例函数  的图象上,
的图象上, 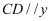 轴,对角线
轴,对角线 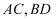 的交点恰好是坐标原点O . 若
的交点恰好是坐标原点O . 若 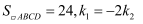 ,则
,则  的值为( )
的值为( )
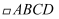 的顶点A , C在反比例函数
的顶点A , C在反比例函数 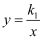 的图象上,顶点B , D在反比例函数
的图象上,顶点B , D在反比例函数  的图象上,
的图象上, 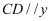 轴,对角线
轴,对角线 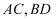 的交点恰好是坐标原点O . 若
的交点恰好是坐标原点O . 若 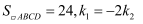 ,则
,则  的值为( )
的值为( ) 
A . 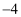 B .
B . 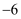 C .
C .  D .
D . 
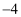 B .
B . 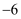 C .
C .  D .
D . 
如图,在▱ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( )

A . 1:3
B . 1:5
C . 1:6
D . 1:11
如图,在距某居民楼AB楼底B点左侧水平距离60m的C点处有一个山坡,山坡CD的坡度(或坡比)i=1:0.75,山坡坡底C点到坡顶D点的距离CD=45m,在坡顶D点处测得居民楼楼顶A点的仰角为28°,居民楼AB与山坡CD的剖面在同一平面内,则居民楼AB的高度约为(参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)( )

A . 76.9m
B . 82.1m
C . 94.8m
D . 112.6m
如图所示几何体是由一个球体和一个圆柱组成的,它的俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,电线杆CD的高度为h,两根拉线AC与BC互相垂直(A、D、B在同一条直线上),设∠CAB=α,那么拉线BC的长度为( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为18cm,那么它在暗盒中所成的像CD的高度应为cm .

如图,在一座山的前方有一栋住宅,已知山高 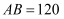 m,楼高
m,楼高 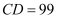 m,某天上午9时太阳光线从山顶点
m,某天上午9时太阳光线从山顶点  处照射到住宅的点
处照射到住宅的点  外.在点
外.在点  处测得点
处测得点  的俯角
的俯角 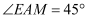 ,上午10时太阳光线从山顶点
,上午10时太阳光线从山顶点  处照射到住宅点
处照射到住宅点  处,在点
处,在点  处测得点
处测得点  的俯角
的俯角 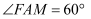 ,已知每层楼的高度为3m,
,已知每层楼的高度为3m, 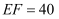 m,问:以当天测量数据为依据,不考虑季节天气变化,至少要买该住宅的第几层楼,才能使上午10时太阳光线照射到该层楼的外墙?(
m,问:以当天测量数据为依据,不考虑季节天气变化,至少要买该住宅的第几层楼,才能使上午10时太阳光线照射到该层楼的外墙?( 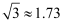 )
)
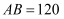 m,楼高
m,楼高 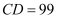 m,某天上午9时太阳光线从山顶点
m,某天上午9时太阳光线从山顶点  处照射到住宅的点
处照射到住宅的点  外.在点
外.在点  处测得点
处测得点  的俯角
的俯角 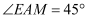 ,上午10时太阳光线从山顶点
,上午10时太阳光线从山顶点  处照射到住宅点
处照射到住宅点  处,在点
处,在点  处测得点
处测得点  的俯角
的俯角 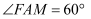 ,已知每层楼的高度为3m,
,已知每层楼的高度为3m, 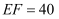 m,问:以当天测量数据为依据,不考虑季节天气变化,至少要买该住宅的第几层楼,才能使上午10时太阳光线照射到该层楼的外墙?(
m,问:以当天测量数据为依据,不考虑季节天气变化,至少要买该住宅的第几层楼,才能使上午10时太阳光线照射到该层楼的外墙?( 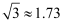 )
) 
函数的自变量x满足  ≤x≤2时,函数值y满足
≤x≤2时,函数值y满足  ≤y≤1,则这个函数可以是( )
≤y≤1,则这个函数可以是( )
 ≤x≤2时,函数值y满足
≤x≤2时,函数值y满足  ≤y≤1,则这个函数可以是( )
≤y≤1,则这个函数可以是( )
A . y=  B . y=
B . y=  C . y=
C . y=  D . y=
D . y= 
 B . y=
B . y=  C . y=
C . y=  D . y=
D . y= 
下面是一天中四个不同时刻两座建筑物的影子,将它们按时间先后顺序正确的是( )
A . (3)(1)(4)(2)
B . (3)(2)(1)(4)
C . (3)(4)(1)(2)
D . (2)(4)(1)(3)
△ABC中,DE∥BC,EF∥AB,已知△ADE和△EFC的面积分别为4和9,则△ABC的面积为 .

如图,一座小山的山顶上有一根竖直的电线杆MN,水平直线AC与MN在同一平面,点B在AC上.用测倾器在点A处测得∠MAC=45°,∠NAC=30°,向前走10米到达点B,在点B处测得∠MBC=60°,∠NBC=45°.求:

-
(1) 电线杆MN的长度;
-
(2) 小山相对于水平直线AC的高度(结果保留根式).
如图,在等腰三角形中,AB=AC,BC=4,D为BC的中点,点E、F在线段AD上,tan∠ABC=3,则阴影部分的面积是

球和圆柱在水平面上紧靠在一起,组成如图所示的几何体,则它的三视图中俯视图应该是( )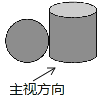
A . 两个相交的圆
B . 两个外切的圆
C . 两个内切的圆
D . 两个外离的圆
如图所示,某河堤的横断面是梯形ABCD,BC∥AD,迎水坡AB长为10米,斜坡AB的坡度i=1: ,则河堤高BE等于( )米
,则河堤高BE等于( )米
A . 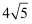 B .
B .  C . 4
D . 5
C . 4
D . 5
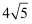 B .
B .  C . 4
D . 5
C . 4
D . 5
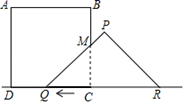
正方形ABCD边长5cm,等腰三角形PQR,PQ=PR=5cm,QR=8cm,点D、C、Q、R在同一直线1上,当C、Q两点重合时,等腰△PQR以1cm/s的速度沿直线1向左方向开始匀速运动,ts后正方形与等腰三角形重合部分面积为Scm2 , 解答下列问题:
-
(1) 当t=3s时,求S的值;
-
(2) 当5s≤t≤8s时,求S与t的函数关系式.
最近更新
- 世界着名的“低地国”是
- 据《史记·吴王濞列传》记载:“上(汉高祖)患吴、会稽轻悍,无壮王以填(镇)之,诸子少,乃立濞于沛为吴王,王三郡五十二城。
- “民间查账人”李德涛依法申请政府信息公开 ,促成了广州市财政局“晒账本”:将114个部门的预算公开放到网上。这说明
- 对于反应CaH2+2H2O=Ca(OH)2+2H2↑,有下列判断:①H2只是氧化产物;②H2只是还原产物;③H2O是氧化
- 心脏结构中,与主动脉相通的是 A.左心房 B.右心房 C.左心室 D.
- (09年江苏模拟)有一种波,其波形为函数的图象,若在区间[0,t]上至少有2个波峰(图象的最高点),则正整数t的最小值是
- For several years, Americans have enjoyed teleshopping—watch
- 1.下列加点词语的读音全都不同的一项是 A.徘徊/低徊 烘焙/赔笑脸 匍匐/果脯 艾草/自怨自艾 B.
- 中国近代早期维新派的形成是在 A.第二次鸦片战争开始后 B.洋务运动开始之时 C.洋务运动开展过程中 D.中日甲
- 恒温动物比变温动物更有生存优势的原因在于( ) A.恒温动物耗氧少 B.恒温动物需要的食物少 C.恒温动物更适应
- 珠穆朗玛峰海拔8844米,死海海拔-400米,两地相对高度是 ( ) A、8844米 B、
- 陕西省北部白于山区39.2万人因干旱缺水和水质差而陷入贫困。2011年陕西省政府决定将他们搬迁到城镇周边、中心村附近或其
- 利用斜二测画法得到的: ①三角形的直观图一定是三角形; ②正方形的直观图一定是菱形; ③等腰梯形的直观图可以是平行四边形
- When the earthquake, a destructive natural disaster, happene
- 若正整数满足:,证明,存在,使以下三式:同时成立.
- 如果要除去CO2气体中混有的少量CO,应该采用的方法是 A、点燃 B、倾倒到另一个容器里 C
- 城市化过程包含了人口城市化和土地城市化等过程。下图示意我国四个省(市、自治区)2000年土地城市化质量的差异。读图完成7
- 两个完全相同的容器中,分别盛有甲、乙两种液体,将完全相同的两个小球分别放入容器中,当小球静止时,液面相平,球所处的位置如
- 下列关于中共七大的表述,正确的有 ( ) ①作了《论联合政府》的报告②大会制定了
- 电磁炮是利用电磁发射技术制成的一种先进的武器,具有速度快、命中率高等优点.它的主要原理如图所示,通电导体在磁场力的作用下



