回归分析 知识点题库
 ,使函数Q(a,b)最小,Q函数指( )
,使函数Q(a,b)最小,Q函数指( ) B .
B .  C .
C .  D .
D . 
(1)若r>0,则x增大时,y也相应增大;
(2)若|r|越趋近于1,则x, y线性相关程度越强;
(3)若r=1或r=-1,则x与y的关系完全对应(有函数关系),在散点图上各个散点均在一条直线上.
其中正确的有( )
 :,且x1+x2+x3+…+x8=2(y1+y2+y3+…+y8)=6,则实数a的值是( )
:,且x1+x2+x3+…+x8=2(y1+y2+y3+…+y8)=6,则实数a的值是( )
 B .
B . 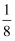 C .
C .  D .
D . 
 =﹣2x+3,则当变量x增加一个单位时,下面结论正确的是( )
=﹣2x+3,则当变量x增加一个单位时,下面结论正确的是( )
x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 74 | 81 | 89 | 90 | 91 |
(1)求纯利y与每天销售件数x之间的回归方程;
(2)若该周内某天销售服装13件,估计可获纯利多少元?
 必过样本点的中心
必过样本点的中心  B . 残差平方和越小的模型,拟合的效果越好
C . 用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好
D . 两个随机变量的线性相关性越强,相关系数的绝对值越接近于1.
B . 残差平方和越小的模型,拟合的效果越好
C . 用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好
D . 两个随机变量的线性相关性越强,相关系数的绝对值越接近于1.
 (数据来源于网络,仅供参考).为了解高三学生对“管理学”的兴趣程度,某校学生社团在高校高三文科班进行了问卷调查,问卷共100道选择题,每题1分,总分100分,社团随机抽取了100名学生的问卷成绩(单位:分)进行统计,得到频率分布表如下:
(数据来源于网络,仅供参考).为了解高三学生对“管理学”的兴趣程度,某校学生社团在高校高三文科班进行了问卷调查,问卷共100道选择题,每题1分,总分100分,社团随机抽取了100名学生的问卷成绩(单位:分)进行统计,得到频率分布表如下:组号 | 分组 | 男生 | 女生 | 频数 | 频率 |
第一组 |
| 3 | 2 | 5 | 0.05 |
第二组 |
| 17 |
|
|
|
第三组 |
| 20 | 10 | 30 | 0.3 |
第四组 |
| 6 | 18 | 24 | 0.24 |
第五组 |
| 4 | 12 | 16 | 0.16 |
合计 | 50 | 50 | 100 | 1 | |

参考公式:  ,其中
,其中  .
.
参考临界值:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
-
(1) 求频率分布表中
 ,
,  ,
,  的值;
的值;
-
(2) 若将得分不低于60分的称为“管理学意向”学生,将低于60分的称为“非管理学意向”学生,根据条件完成下面
 列联表,并据此判断是否有
列联表,并据此判断是否有  的把握认为是否为“管理学意向”与性别有关?
的把握认为是否为“管理学意向”与性别有关?非管理学意向
管理学意向
合计
男生


女生


合计
-
(3) 心理咨询师认为得分低于20分的学生可能“选择困难”,要从“选择困难”的5名学生中随机抽取2名学生进行心理辅导,求恰好有1名男生,1名女生被选中的概率.
 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( ) C . 若该大学某女生身高增加1 cm,则其体重约增加0.85 kg
D . 若该大学某女生身高为170 cm,则可断定其体重必为58.79 kg
C . 若该大学某女生身高增加1 cm,则其体重约增加0.85 kg
D . 若该大学某女生身高为170 cm,则可断定其体重必为58.79 kg
 (单位:吨)对价格
(单位:吨)对价格  (单位:千元/吨)和利润
(单位:千元/吨)和利润  的影响,对近五年该农产品的年产量和价格统计如下表:
的影响,对近五年该农产品的年产量和价格统计如下表:
| 1 | 2 | 3 | 4 | 5 |
| 8 | 6 | 5 | 4 | 2 |
已知  和
和  具有线性相关关系.
具有线性相关关系.
-
(1) 求
 关于
关于  的线性回归方程
的线性回归方程  ;
;
-
(2) 若每吨该农产品的成本为2.2千元,假设该农产品可全部卖出,预测当年产量为多少吨时,年利润
 取到最大值?
取到最大值?参考公式:
 .
.
 与物理成绩
与物理成绩  如下表:
如下表:
数据表明  与
与  之间有较强的线性关系.
之间有较强的线性关系.
参考数据:回归直线的系数  ,
,  .
.
 ,
,  .
.
-
(1) 求
 关于
关于  的线性回归方程;
的线性回归方程;
-
(2) 该班一名同学的数学成绩为110分,利用(1)中的回归方程,估计该同学的物理成绩;
-
(3) 本次考试中,规定数学成绩达到125分为优秀,物理成绩达到100分为优秀.若该班数学优秀率与物理优秀率分别为
 和
和  ,且除去抽走的5名同学外,剩下的同学中数学优秀但物理不优秀的同学共有5人.能否在犯错误概率不超过0.01的前提下认为数学优秀与物理优秀有关?
,且除去抽走的5名同学外,剩下的同学中数学优秀但物理不优秀的同学共有5人.能否在犯错误概率不超过0.01的前提下认为数学优秀与物理优秀有关?
 (单位:
(单位:  )与孵化天数
)与孵化天数  之间的关系,某课外兴趣小组通过试验得到如下6组数据:
之间的关系,某课外兴趣小组通过试验得到如下6组数据:组号 | 1 | 2 | 3 | 4 | 5 | 6 |
平均温度 | 15.3 | 16.8 | 17.4 | 18 | 19.5 | 21 |
孵化天数 | 16.7 | 14.8 | 13.9 | 13.5 | 8.4 | 6.2 |
他们分别用两种模型①  ,②
,②  分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图:

经计算得  ,
,
-
(1) 根据残差图,比较模型①,②的拟合效果,应选择哪个模型?(给出判断即可,不必说明理由)
-
(2) 残差绝对值大于1的数据被认为是异常数据,需要剔除,剔除后应用最小二乘法建立
 关于
关于  的线性回归方程.(精确到0.1)
的线性回归方程.(精确到0.1) ,.
,.
 (单位:万元)的数据如下表,已知
(单位:万元)的数据如下表,已知  与
与  具有较好的线性关系.
具有较好的线性关系.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
 ,
,  .
.
-
(1) 求
 关于
关于  的线性回归方程;
的线性回归方程;
-
(2) 分析该淘宝商城2017年前7个月的销售额的变化情况,并预测该商城8月份的销售额.
 与
与  之间的数据如下表:
之间的数据如下表:
|
|
|
|
|
|
|
|
|
|
|
|
附: 
 ,
,  ,
,  ,
,  .
.
-
(1) 求
 关于
关于  的线性回归方程;
的线性回归方程;
-
(2) 完成下面的残差表:







并判断(1)中线性回归方程的回归效果是否良好(若
 ,则认为回归效果良好).
,则认为回归效果良好).
①从匀速传递的产品生产流水线上,每20分钟从中抽取一件产品进行检测,这样的抽样是分层抽样。②两个随机变量的线性相关性越强,则相关系数的绝对值越接近于1。
③在线性回归方程  中,当解释变量
中,当解释变量  每增加一个单位时,预报变量
每增加一个单位时,预报变量  平均增加0.2个单位。④分类变量
平均增加0.2个单位。④分类变量  与
与  ,它们的随机变量
,它们的随机变量  的观测值为
的观测值为  ,当
,当  越小,“
越小,“  与
与  有关系”的把握程度越大。
有关系”的把握程度越大。
①相关系数  用来衡量两个变量之间线性关系的强弱,
用来衡量两个变量之间线性关系的强弱,  越接近于1,相关性越弱;
越接近于1,相关性越弱;
②回归直线  过样本点中心
过样本点中心  ;
;
③相关指数  用来刻画回归的效果,
用来刻画回归的效果,  越小,说明模型的拟合效果越不好.
越小,说明模型的拟合效果越不好.
 的值不能由解释变量
的值不能由解释变量  唯一确定
B . 若变量
唯一确定
B . 若变量  ,
,  满足关系
满足关系  ,且变量
,且变量  与
与  正相关,则
正相关,则  与
与  也正相关
C . 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D . 以模型
也正相关
C . 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D . 以模型  去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设  ,将其变换后得到线性方程
,将其变换后得到线性方程  ,则
,则  ,
, 
 和温度
和温度  有关.现收集了7组观测数据如下表:
有关.现收集了7组观测数据如下表: | 温度 | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
| 产卵数 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
为了预报一只红玲虫在  时的产卵数,根据表中的数据建立了
时的产卵数,根据表中的数据建立了  与
与  的两个回归模型.模型①:先建立
的两个回归模型.模型①:先建立  与
与  的指数回归方程
的指数回归方程  ,然后通过对数变换
,然后通过对数变换  ,把指数关系变为
,把指数关系变为 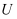 与
与  的线性回归方程:
的线性回归方程:  ;模型②:先建立
;模型②:先建立  与
与  的二次回归方程
的二次回归方程  ,然后通过变换
,然后通过变换  ,把二次关系变为
,把二次关系变为  与
与  的线性回归方程:
的线性回归方程:  .
.
-
(1) 分别利用这两个模型,求一只红玲虫在
 时产卵数的预测值;
时产卵数的预测值;
-
(2) 你认为用哪个模型得到的预测值更可靠?并说明理由.(参考数据:模型①的残差平方和
 ,模型①的相关指数
,模型①的相关指数  ;模型②的残差平方和
;模型②的残差平方和  ,模型②的相关指数
,模型②的相关指数  ;
;  ,
,  ,
,  ;
;  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  )
)
|
单价 | 14 | 16 | 18 | 20 | 22 |
| 销量 | 12 | 10 | 7 | 5 | 3 |
-
(1) 求回归直线方程
 .
.
-
(2) 利用
 刻画回归效果.
刻画回归效果.
 与一定范围内的温度
与一定范围内的温度  有关,于是科研人员在3月份的31天中随机挑选了5天进行研究,现收集了该种药用昆虫的5组观测数据如下表:
有关,于是科研人员在3月份的31天中随机挑选了5天进行研究,现收集了该种药用昆虫的5组观测数据如下表: | 日期 | 2日 | 7日 | 15日 | 22日 | 30日 |
| 温度 | 10 | 11 | 13 | 12 | 8 |
| 产卵数 | 23 | 25 | 30 | 26 | 16 |
附:回归直线的斜率和截距的最小二乘估计公式分别为  ,
,  .
.
-
(1) 从这5天中任选2天,记这两天药用昆虫的产卵分别为
 ,
,  ,求事件“
,求事件“  ,
,  均不小于25”的概率;
均不小于25”的概率;
-
(2) 科研人员确定的研究方案是:先从这五组数据中任选2组,用剩下的3组数据建立
 关于
关于  的线性回归方程,再对被选取的2组数据进行检验.
的线性回归方程,再对被选取的2组数据进行检验. (ⅰ)若选取的是3月2日与30日的两组数据,请根据3月7日、15日和22日这三天的数据,求出
 关于
关于  的线性回归方程;
的线性回归方程;(ⅱ)若由线性回归方程得到的估计数据与选出的检验数据的误差均不超过2个,则认为得到的线性回归方程是可靠的,试问(ⅰ)中所得的线性回归方程是否可靠?
- 小雨阅读课外资料得知,双氧水分解除了用二
- 角α的终边落在区间(-3π,-π)内,则角α所
- 人的体细胞含有23对染色体,在减数第二次分
- 杜甫《望岳》“会当凌绝顶,一览众山小&r
- A_____girl named Dong Xinyi looked after her disabled fath
- 一位同学参加中央电视台“开心辞典”网上
- 阅读还原: When I was about 12, I had an enemy, a girl
- 为了防止水的污染,我国许多地区对洗衣粉生
- 如图,△ABC中,∠BAC=90°,正方形的一边GF在BC
- 2013年12月11日深圳光明批发市场发生重大火灾
- 如图为家鸽的呼吸系统和气囊结构示意图,能
- 如图所示,理想变压器的原、副线圈匝数比为
- CCTV“人与自然”节目报道,1998年8月湖北省麋
- 根据对话内容,从方框里选出五个合适的句子
- 为了预防、控制艾滋病的发生与流行,保障人
- My sister started ice skating ____she was four.A. because �
- 我们打篮球的时间到了。 (time)
- 青青草原上,灰太狼每天都想着如何抓羊,而
- 完形填空On the afternoon of March 11th, 2011, Japan, Da
- 12.下列各组句子中,加点词语的意义与现代
















