回归分析 知识点题库
①最小二乘法指的是把各个离差加起来作为总离差,并使之达到最小值的方法;
②最小二乘法是指把各离差的平方和作为总离差,并使之达到最小值的方法;
③线性回归就是由样本点去寻找一条直线,贴近这些样本点的数学方法;
④因为由任何一观测值都可以求得一个回归直线方程,所以没有必要进行相关性检验.
 必过定点( )
必过定点( )
 C .
C .  D .
D . 
①函数关系是一种确定性关系;②相关关系是一种非确定性关系;③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法
①x1+x2+x3+x4=18,y1+y2+y3+y4=14;
②广告费用x和销售额y之间具有较强的线性相关关系;
③回归直线方程 =bx+a中的b=0.8(用最小二乘法求得);
=bx+a中的b=0.8(用最小二乘法求得);
那么,当广告费用为6千元时,可预测销售额约为( )
 =0.9x+0.2(单位:亿元),预计今年该城市居民年收入为20亿元,则年支出估计是 亿元.
=0.9x+0.2(单位:亿元),预计今年该城市居民年收入为20亿元,则年支出估计是 亿元.
x | 0 | 1 | 3 | 4 |
y | 2.2 | 4.3 | 4.8 | 6.7 |
从散点图分析,y与x线性相关,则回归方程为 =bx+a必过点
=bx+a必过点
①某校高三一班和高三二班的人数分别是m,n,某次测试数学平均分分别是a,b,则这两个班的数学平均分为 ;
;
②10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有c>a>b;
③从总体中抽取的样本(x1 , y1),(x2 , y2),…,(xn , yn),若记 =
=
 xi ,
xi ,  =
=
 yi则回归直线y=bx+a必过点(
yi则回归直线y=bx+a必过点( ,
, );
);
④已知ξ服从正态分布N(0,σ2),且p(﹣2≤ξ≤0)=0.3,则p(ξ>2)=0.2;
其中正确的个数有( )
比分 | 易建联技术统计 | |||
投篮命中 | 罚球命中 | 全场得分 | 真实得分率 | |
中国91﹣42新加坡 | 3/7 | 6/7 | 12 | 59.52% |
中国76﹣73韩国 | 7/13 | 6/8 | 20 | 60.53% |
中国84﹣67约旦 | 12/20 | 2/5 | 26 | 58.56% |
中国75﹣62哈萨克期坦 | 5/7 | 5/5 | 15 | 81.52% |
中国90﹣72黎巴嫩 | 7/11 | 5/5 | 19 | 71.97% |
中国85﹣69卡塔尔 | 4/10 | 4/4 | 13 | 55.27% |
中国104﹣58印度 | 8/12 | 5/5 | 21 | 73.94% |
中国70﹣57伊朗 | 5/10 | 2/4 | 13 | 55.27% |
中国78﹣67菲律宾 | 4/14 | 3/6 | 11 | 33.05% |
注:(1)表中a/b表示出手b次命中a次;
(2)TS%(真实得分率)是衡量球员进攻的效率,其计算公式为:
TS%=.全场得分/2x(投篮出手次数+0.44x罚球出手次数)
(Ⅰ)从上述9场比赛中随机选择一场,求易建联在该场比赛中TS%超过50%的概率;
(Ⅱ)从上述9场比赛中随机选择两场,求易建联在这两场比赛中TS%至少有一场超过60%的概率;
(Ⅲ)用x来表示易建联某场的得分,用y来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断y与x之间是否具有线性相关关系?结合实际简单说明理由.

 =0.95x+a,则a=( )
=0.95x+a,则a=( )x | 0 | 1 | 3 | 4 |
y | 2.2 | 4.3 | 4.8 | 6.7 |
 的经营状况,对该公司最近六个月内的市场占有率进行了统计,并绘制了相应的折线图.
的经营状况,对该公司最近六个月内的市场占有率进行了统计,并绘制了相应的折线图. 
(Ⅰ)由折线图得,可用线性回归模型拟合月度市场占有率  与月份代码
与月份代码  之间的关系.求
之间的关系.求  关于
关于  的线性回归方程,并预测
的线性回归方程,并预测  公司2017年5月份(即
公司2017年5月份(即  时)的市场占有率;
时)的市场占有率;

(Ⅱ)为进一步扩大市场,公司拟再采购一批单车.现有采购成本分别为1000元/辆和1200元/辆的  两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不形同,考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表见上表.
两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不形同,考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表见上表.
经测算,平均每辆单车每年可以带来收入500元,不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整年,且以频率作为每辆单车使用寿命的概率,如果你是  公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
(参考公式:回归直线方程为  ,其中
,其中  )
)
 (单位:
(单位: 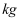 )与身高
)与身高  (单位:
(单位: 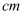 )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据  ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为  ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
 与
与  具有正的线性相关关系
B . 回归直线过样本点的中心
具有正的线性相关关系
B . 回归直线过样本点的中心  C . 若该大学某女生身高增加
C . 若该大学某女生身高增加  ,则其体重约增加
,则其体重约增加  D . 若该大学某女生身高为
D . 若该大学某女生身高为  ,则可断定其体重必为
,则可断定其体重必为 
|
日期 |
1月10号 |
2月10号 |
3月10号 |
4月10号 |
5月10号 |
6月10号 |
|
昼夜温差x(℃) |
10 |
11 |
13 |
12 |
8 |
6 |
|
就诊人数y(人) |
22 |
25 |
29 |
26 |
16 |
12 |
该兴趣小组确定的研究方案是先从这6组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选出的2组数据进行检验.
附; 
-
(1) 若选取的是1月和6月的两组数据,请根据2月至5月的数据求出
 关
关  于的线性回归方程;
于的线性回归方程;
-
(2) 若由线性回归方程得到的估计数,与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的.试问:该小组所得的线性回归方程是否理想?
 ,模型②:
,模型②:  ,对以上两个回归方程进行残差分析,得到下表:
,对以上两个回归方程进行残差分析,得到下表: | 种植面积 | 2 | 3 | 4 | 5 | 7 | 9 | |
| 每亩种植管理成本 | 25 | 24 | 21 | 22 | 16 | 14 | |
| 模型① | 估计值 | 25.27 | 23.62 | 21.97 | 17.02 | 13.72 | |
| 残差 | -0.27 | 0.38 | -0.97 | -1.02 | 0.28 | ||
| 模型② | | 26.84 | 20.17 | 18.83 | 17.31 | 16.46 | |
| | -1.84 | 0.83 | 3.17 | -1.31 | -2.46 | ||
-
(1) 将以上表格补充完整,并根据残差平方和判断哪个模型拟合效果更好;
-
(2) 视残差
 的绝对值超过1.5的数据视为异常数据,针对(1)中拟合效果较好的模型,剔除异常数据后,重新求回归方程.
的绝对值超过1.5的数据视为异常数据,针对(1)中拟合效果较好的模型,剔除异常数据后,重新求回归方程. 附:
 ,
,  ;
; 
 (单位:万元)与纯利润
(单位:万元)与纯利润  (单位:万元)的数据进行整理后,得到如下表格:
(单位:万元)的数据进行整理后,得到如下表格: | 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 销售收入 | 13 | 13.5 | 13.8 | 14 | 14.2 | 14.5 | 15 |
| 纯利润 | 3.2 | 3.8 | 4 | 4.2 | 4.5 | 5 | 5.5 |
该公司先从这7组数据中选取5组数据求纯利润  关于销售收入
关于销售收入  的线性回归方程,再用剩下的2组数据进行检验.假设选取的是2月至6月的数据.
的线性回归方程,再用剩下的2组数据进行检验.假设选取的是2月至6月的数据.
参考公式:  ,
,  ,
,  ,
,  ;参考数据:
;参考数据:  .
.
-
(1) 求纯利润
 关于销售收入
关于销售收入  的线性回归方程(精确到0.01);
的线性回归方程(精确到0.01);
-
(2) 若由线性回归方程得到的估计数据与检验数据的误差均不超过0.1万元,则认为得到的线性回归方程是理想的.试问该公司所得线性回归方程是否理想?
|
年份 |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
|
年份代码x |
1 |
2 |
3 |
4 |
5 |
6 |
|
新能源乘用车年销售y(万辆) |
50 |
78 |
126 |
121 |
137 |
352 |
参考数据:设u=lny,其中ui=lnyi .
|
|
|
|
|
e3.63 |
e5.94 |
e6.27 |
|
144 |
4.78 |
841 |
5.70 |
37.71 |
380 |
528 |
参考公式:对于一组具有线性相关关系的数据(xi , yi)(i=1,2,3,⋅⋅⋅,n),其回归直线  的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为  ,
,  .
.
-
(1) 根据表中数据,求出y关于x的线性回归方程;(结果保留整数)
-
(2) 若用y=menx模型拟合y与x的关系,可得回归方程为
 ,请分别利用(1)与(2)中两个模型,求2022年我国新能源乘用车的年销售量的预测值;
,请分别利用(1)与(2)中两个模型,求2022年我国新能源乘用车的年销售量的预测值;
- 关于化学能与热能的叙述,正确的是A.1mol酸
- Right now the government is trying to control the number of
- 下列各组中的三种微粒,所含质子数与电子数
- 生物多样性是共同进化的结果。下列事实不属
- 下列各种生物中,属于生产者的是 �
- 以下表示氦原子结构的化学用语中,对电子运
- 下列运算正确的是( ) A.x3•x3=2x6
- 1791年的一天,法国巴黎60多万人迎送一位哲人
- 如图所示,带箭头的曲线表示一个带负电粒子
- 下列四种病毒中,遗传信息贮存在DNA分子中的
- 一般情况下,胶体粒子不易聚集而稳定,主要
- ______ are you doing this evening? A.How B
- 水是人类宝贵的自然资源。下列有关水的说法
- 某人在如图3所示的直角边长为4米的三角形地
- (12分) 在常温下,Fe与水并不起反应,但在
- 有3人排成一排,甲、乙两人不相邻的概率是(
- 日本帝国主义制造“九一八”事变的直接原因
- __________,长河落日圆。
- 对于把人或哺乳动物的成熟红细胞作为获取细
- 《水调歌头·明月几时有》中从“隔千里兮并











