回归分析知识点题库

在建立两个变量Y与x的回归模型中，分别选择了4个不同模型，它们的相关指数R²如下，其中拟合得最好的模型是 ( )

A . 模型1的相关指数R²为0.98 B . 模型2的相关指数R²为0.80 C . 模型3的相关指数R²为0.50 D . 模型4的相关指数R²为0.25

下列结论中正确的个数是（）
（1）在回归分析中，可用指数系数 $\text{[math]}$ 的值判断模型的拟合效果， $\text{[math]}$ 越大，模型的拟合效果越好；
（2）在回归分析中，可用残差平方和判断模型的拟合效果，残差平方和越大，模型的拟合效果越好；
（3）在回归分析中，可用相关系数r的值判断模型的拟合效果，r越小，模型的拟合效果越好；
（4）在回归分析中，可用残差图判断模型的拟合效果，残差点比较均匀地落在水平的带状区域中，说明这样的模型比较合适．带状区域的宽度越窄，说明模型的拟合精度越高．

A . 1 B . 2 C . 3 D . 4

有下列说法：①在残差图中，残差点比较均匀地落在水平的带状区域内，说明选用的模型比较合适．②相关指数 $\text{[math]}$ 来刻画回归的效果， $\text{[math]}$ 值越小，说明模型的拟合效果越好．③比较两个模型的拟合效果，可以比较残差平方和的大小，残差平方和越小的模型，拟合效果越好．其中正确命题的个数是（　　）

A . 0 B . 1 C . 2 D . 3

某车间加工零件的数量x与加工时间y的统计数据如下表：

零件数x（个）	11	20	29
加工时间y（分钟）	20	31	39

现已求得上表数据的回归方程 $\text{[math]}$ =bx+a中的b的值为0.9，则据此回归模型可以预测，加工90个零件所需要的加工时间约为（）

A . 93分钟 B . 94分钟 C . 95分钟 D . 96分钟

对两个变量y与x进行回归分析，分别选择不同的模型，它们的相关系数r如下，其中拟合效果最好的模型是（　　）

①模型Ⅰ的相关系数r为﹣0.98；

②模型Ⅱ的相关系数r为0.80；

③模型Ⅲ的相关系数r为﹣0.50；

④模型Ⅳ的相关系数r为0.25．

A . ① B . ② C . ③ D . ④

对于回归分析，下列说法错误的是（　　）

A . 在回归分析中，变量间的关系若是非确定关系，那么因变量不能由自变量唯一确定 B . 样本相关系数r∈（﹣1，1） C . 回归分析中，如果r²=1，说明x与y之间完全相关 D . 线性相关系数可以是正的，也可以是负的

给出下列四个命题：

①由样本数据得到的回归方程 $\text{[math]}$ 必过样本点的中心（ $\text{[math]}$ ， $\text{[math]}$ ）；

②用相关指数R²来刻画回归效果，R²的值越小，说明模型的拟合效果越好；

③若线性回归方程为 $\text{[math]}$ =3﹣2.5x，则变量x每增加1个单位时，y平均减少2.5个单位；

④在残差图中，残差点分布的带状区域的宽度越窄，残差平方和越小．

上述四个命题中，正确命题的个数为（）

A . 1 B . 2 C . 3 D . 4

两个变量y与x的回归模型中，分别选择了4个不同模型，它们对应的回归系数r如下，其中变量之间线性相关程度最高的模型是（）

A . 模型1对应的r为﹣0.98 B . 模型2对应的r为0.80 C . 模型3对应的r为0.50 D . 模型4对应的r为﹣0.25

已知某商品的价格 $\text{[math]}$ （元）与需求量 $\text{[math]}$ （件）之间的关系有如下一组数据：

x	14	16	18	20	22
y	12	10	7	5	3

（参考公式： $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ ）

参考数据： $\text{[math]}$

当n-2=3， $\text{[math]}$ ,

（1）求 $\text{[math]}$ , $\text{[math]}$ ;
（2）求出回归直线方程
（3）计算相关系数r的值，并说明回归模型拟合程度的好坏。

在对具有线性相关的两个变量 $\text{[math]}$ 和 $\text{[math]}$ 进行统计分析时，得到如下数据：

$\text{[math]}$	4	$\text{[math]}$	8	10	12
$\text{[math]}$	1	2	3	5	6

由表中数据求得 $\text{[math]}$ 关于 $\text{[math]}$ 的回归方程为 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 这三个样本点中落在回归直线下方的有( )个

A . 1 B . 2 C . 3 D . 0

张三同学从每年生日时对自己的身高测量后记录如表：

$\text{[math]}$

（附：回归直线的斜率和截距的最小二乘法估计公式分别为： $\text{[math]}$ ， $\text{[math]}$ ）

（1）求身高 $\text{[math]}$ 关于年龄 $\text{[math]}$ 的线性回归方程；(可能会用到的数据： $\text{[math]}$ （cm）)
（2）利用（1）中的线性回归方程，分析张三同学 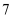$\text{[math]}$ 岁起到 $\text{[math]}$ 岁身高的变化情况，如 $\text{[math]}$ 岁之前都符合这一变化，请预测张三同学 $\text{[math]}$ 岁时的身高。

一只药用昆虫的产卵数 $\text{[math]}$ 与一定范围内的温度 $\text{[math]}$ 有关，现收集了该种药用昆虫的6组观测数据如下表：

温度 $\text{[math]}$	21	23	24	27	29	32
产卵数 $\text{[math]}$ /个	6	11	20	27	57	77

附：一组数据 $\text{[math]}$ ，其回归直线 $\text{[math]}$ 的斜率和截距的最小二乘估计为 $\text{[math]}$ ；相关指数 $\text{[math]}$ .

$\text{[math]}$

（1）若用线性回归模型，求 $\text{[math]}$ 关于 $\text{[math]}$ 的回归方程 $\text{[math]}$ （精确到0.1）；
（2）若用非线性回归模型求 $\text{[math]}$ 关 $\text{[math]}$ 的回归方程为 $\text{[math]}$ ，且相关指数 $\text{[math]}$
①试与（1）中的线性回归模型相比，用 $\text{[math]}$ 说明哪种模型的拟合效果更好.
②用拟合效果好的模型预测温度为 $\text{[math]}$ 时该种药用昆虫的产卵数（结果取整数）.

变量X与Y相对应的5组数据和变量U与V相对应的5组数据统计如下表：

X	10	11.3	11.8	12.5	13		U	10	11.3	11.8	12.5	13
Y	1	2	3	4	5		V	5	4	3	2	1

用b₁表示变量Y与X之间的回归系数，b₂表示变量V与U之间的回归系数，则b₁与b₂的大小关系是。

下列关于残差图的描述错误的是（）

A . 残差图的横坐标可以是编号 B . 残差图的横坐标可以是解释变量和预报变量 C . 残差点分布的带状区域的宽度越窄相关指数越小 D . 残差点分布的带状区域的宽度越窄残差平方和越小

下列说法中正确的是（）

A . 在频率分布直方图中，中位数左边和右边的直方图的面积相等. B . 若A、B为互斥事件，则A的对立事件与B的对立事件一定互斥. C . 某个班级内有40名学生，抽10名同学去参加某项活动，则每4人中必有1人抽中. D . 若回归直线 $\text{[math]}$ 的斜率 $\text{[math]}$ ，则变量 $\text{[math]}$ 与 $\text{[math]}$ 正相关.

①回归分析中，相关指数 $\text{[math]}$ 的值越大，说明残差平方和越大；

②对于相关系数 $\text{[math]}$ ， $\text{[math]}$ 越接近1，相关程度越大， $\text{[math]}$ 越接近0，相关程度越小；

③有一组样本数据 $\text{[math]}$ 得到的回归直线方程为 $\text{[math]}$ ，那么直线 $\text{[math]}$ 必经过点 $\text{[math]}$ ；

④ $\text{[math]}$ 是用来判断两个分类变量是否有关系的随机变量，只对于两个分类变量适合；

以上几种说法正确的序号是．

近日，为进一步做好新冠肺炎疫情防控工作，某社区以网上调查问卷形式对辖区内部分居民做了新冠疫苗免费接种的宣传和调查．调查数据如下：共95份有效问卷，40名男性中有10名不愿意接种疫苗，55名女性中有5名不愿意接种疫苗．

（1）根据所给数据，完成下面的2×2列联表，并根据列联表，判断是否有95%的把握认为是否愿意接种疫苗与性别有关？

	愿意接种	不愿意接种	合计
男
女
合计

（2）从不愿意接种的15份调查问卷中得到拒绝接种新冠疫苗的原因：有3份身体原因不能接种；有2份认为新冠肺炎已得到控制，无需接种；有4份担心疫苗的有效性；有6份担心疫苗的安全性．求从这15份问卷中随机选出2份，在已知至少有一份担心疫苗安全性的条件下，另一份是担心疫苗有效性的概率．
附： $\text{[math]}$

P（K²≥k）

0.050 0.010 0.005

k

3.841 6.635 7.879

下列关于回归分析的说法中错误的是（）

A . 回归直线一定过样本中心 $\text{[math]}$ B . 残差图中残差点比较均匀地落在水平的带状区域中，说明选用的模型比较合适 C . 甲、乙两个模型的 $\text{[math]}$ 分别约为 $\text{[math]}$ 和 $\text{[math]}$ ，则模型乙的拟合效果更好 D . 两个模型中残差平方和越小的模型拟合的效果越好