回归分析 知识点题库
①将一组数据中的每一个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程
 , 变量x增加一个单位时,y平均增加5个单位;
, 变量x增加一个单位时,y平均增加5个单位;③相关系数r越接近1,说明模型的拟和效果越好;
其中错误的个数是( )
x | 1 | 2 | 3 | 4 | 10 |
y | 2 | 4 | 10 | 8 | 12 |
去掉其中一组后,剩下的4组数据的线性相关性最强,则应去掉的一组数据所对应的点是( )
单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
由表中数据,求得线性回归方程为  =﹣4x+a.若在这些样本点中任取一点,则它在回归直线左下方的概率为 ( )
=﹣4x+a.若在这些样本点中任取一点,则它在回归直线左下方的概率为 ( )
 B .
B .  C .
C .  D .
D . 
印刷册数 (千册) | 2 | 3 | 4 | 5 | 8 |
单册成本 (元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:  =
=  ,方程乙:
,方程乙:  =
=  .
.
-
(1) 为了评价两种模型的拟合效果,完成以下任务.
完成下表(计算结果精确到0.1);
印刷册数x(千册)
2
3
4
5
8
单册成本y(元)
3.2
2.4
2
1.9
1.7
模型甲
估计值

2.4
2.1
1.6
残差

0
﹣0.1
0.1
模型乙
估计值

2.3
2
1.9
残差

0.1
0
0
-
(2) 分别计算模型甲与模型乙的残差平方和Q1及Q2 , 并通过比较Q1 , Q2的大小,判断哪个模型拟合效果更好.
-
(3) 该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷.根据市场调查,新需求量为8千册(概率0.8)或10千册(概率0.2),若印刷厂以每册5元的价格将书籍出售给订货商,问印刷厂二次印刷8千册还是10千册能获得更多利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本)
连锁店 | A店 | B店 | C店 | |||
售价x(元) | 80 | 86 | 82 | 88 | 84 | 90 |
销量y(件) | 88 | 78 | 85 | 75 | 82 | 66 |
-
(1) 分别以三家连锁店的平均售价与平均销量为散点,求出售价与销量的回归直线方程
 ;
;
-
(2) 在大量投入市场后,销量与单价仍然服从(1)中的关系,且该夏装成本价为40元/件,为使该新夏装在销售上获得最大利润,该款夏装的单价应定为多少元?(保留整数)
附:

价格x/元 | 14 | 16 | 18 | 20 | 22 |
需求量y/件 | 56 | 50 | 43 | 41 | 37 |
求出y关于x的线性回归方程,并说明拟合效果的好坏.
(参考数据:  )
)
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
不“礼让斑马线”驾驶员人数 | 120 | 105 | 100 | 85 | 90 | 80 |
(Ⅰ)请根据表中所给前5个月的数据,求不“礼让斑马线”的驾驶员人数  与月份
与月份  之间的回归直线方程
之间的回归直线方程  ;
;
(Ⅱ)若该十字路口某月不“礼让斑马线”驾驶员人数的实际人数与预测人数之差小于5,则称该十字路口“礼让斑马线”情况达到“理想状态”.试根据(Ⅰ)中的回归直线方程,判断6月份该十字路口“礼让斑马线”情况是否达到“理想状态”?
(Ⅲ)若从表中3、4月份分别选取4人和2人,再从所选取的6人中任意抽取2人进行交规调查,求抽取的两人恰好来自同一月份的概率.
参考公式: 
 ,
,  .
.
 与销售额
与销售额  进行了统计,发现其呈线性正相关,统计数据如下表:
进行了统计,发现其呈线性正相关,统计数据如下表:广告费用 | 2 | 3 | 4 | 5 |
销售额 | 26 | 39 | 49 | 54 |
根据上表可得回归方程  ,据此模型可预测广告费为6万元的销售额为( )
,据此模型可预测广告费为6万元的销售额为( )
 80,90
80,90  、
、  90,100
90,100  、
、  100,110
100,110  、
、  110,120
110,120  、
、  120,130
120,130  ,由此得到两个班测试成绩的频率分布直方图:
,由此得到两个班测试成绩的频率分布直方图:
附:
 ,其中
,其中 
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5. 024 | 6.635 | 7.879 | 10.828 |
-
(1) 完成下面2×2列联表,你能有97.5
 的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;成绩小于100分
成绩不小于100分
合计
甲班


50
乙班


50
合计


100
-
(2) 根据所给数据可估计在这次测试中,甲班的平均分是105.8,请你估计乙班的平均分,并计算两班平均分相差几分?
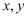 得到一组样本数据,进行回归分析,有以下结论
得到一组样本数据,进行回归分析,有以下结论 ①残差平方和越小的模型,拟合的效果越好;②用相关指数  来刻画回归效果,
来刻画回归效果,  越小说明拟合效果越好;③在回归直线方程
越小说明拟合效果越好;③在回归直线方程  中,当解释变量
中,当解释变量  每增加1个单位时,预报变量
每增加1个单位时,预报变量  平均增加0.2个单位④若变量
平均增加0.2个单位④若变量  和
和  之间的相关系数为
之间的相关系数为  ,则变量
,则变量  和
和  之间的负相关很强,以上正确说法的个数是( )
之间的负相关很强,以上正确说法的个数是( )
 与乘客等候人数
与乘客等候人数  之间的关系,经过调查得到如下数据:
之间的关系,经过调查得到如下数据: | 间隔时间/分 | 10 | 11 | 12 | 13 | 14 | 15 |
| 等候人数y/人 | 23 | 25 | 26 | 29 | 28 | 31 |
调查小组先从这  组数据中选取
组数据中选取  组数据求线性回归方程,再用剩下的
组数据求线性回归方程,再用剩下的  组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数
组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数  ,再求
,再求  与实际等候人数
与实际等候人数  的差,若差值的绝对值都不超过
的差,若差值的绝对值都不超过  ,则称所求方程是“恰当回归方程”.
,则称所求方程是“恰当回归方程”.
-
(1) 从这
 组数据中随机选取2组数据,求选取的这
组数据中随机选取2组数据,求选取的这  组数据的间隔时间不相邻的概率;
组数据的间隔时间不相邻的概率;
-
(2) 若选取的是后面
 组数据,求
组数据,求  关于
关于  的线性回归方程
的线性回归方程  ,并判断此方程是否是“恰当回归方程”;
,并判断此方程是否是“恰当回归方程”; 附:对于一组数据
 ,
,  ,……,
,……,  ,其回归直线
,其回归直线  的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: 
 ,
,  .
.
①若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差不变;②在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;③若两个变量间的线性相关关系越强,则相关系数  的值越接近于1;④对分类变量
的值越接近于1;④对分类变量  与
与  的随机变量
的随机变量  的观测值
的观测值  来说,
来说,  越小,判断“
越小,判断“  与
与  有关系”的把握越大.其中正确的命题序号是( )
有关系”的把握越大.其中正确的命题序号是( )

①.残差图中残差点所在的水平带状区域越宽,则回归方程的预报精确度越高.②.回归直线一定过样本中心(  ,
,  ).③.两个模型中残差平方和越小的模型拟合的效果越好.④.甲、乙两个模型的R2分别约为0.88和0.80,则模型乙的拟合效果更好.
).③.两个模型中残差平方和越小的模型拟合的效果越好.④.甲、乙两个模型的R2分别约为0.88和0.80,则模型乙的拟合效果更好.
 的绝对值越小,说明拟合效果越好;
的绝对值越小,说明拟合效果越好; ②以模型  去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设  ,将其变换后得到线性方程
,将其变换后得到线性方程  ,则
,则  ,
,  的值分别是
的值分别是  和
和 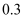 ;
;
③已知随机变量  ,若
,若  ,则
,则  的值为
的值为  ;
;
④通过回归直线  及回归系数
及回归系数  ,可以精确反映变量的取值和变化趋势.
,可以精确反映变量的取值和变化趋势.
其中正确的选项是( )
 的斜率
的斜率  ,则变量
,则变量  与
与  正相关
正相关
 ,
,  , 则
, 则 B . 设随机变量X服从正态分布
B . 设随机变量X服从正态分布 , 则
, 则 C . 在回归分析中,对一组给定的样本数据
C . 在回归分析中,对一组给定的样本数据 而言,当样本相关系数
而言,当样本相关系数 越接近1时,样本数据的线性相关程度越强
D . 在回归分析中,对一组给定的样本数据
越接近1时,样本数据的线性相关程度越强
D . 在回归分析中,对一组给定的样本数据 而言,若残差平方和越大,则模型的拟合效果越差;反之,则模型的拟合效果越好
而言,若残差平方和越大,则模型的拟合效果越差;反之,则模型的拟合效果越好
 越大,说明回归效果越好
B . 已知
越大,说明回归效果越好
B . 已知 , 若根据2×2列联表得到
, 若根据2×2列联表得到 的观测值为4.1,则有95%的把握认为两个分类变量有关
C . 已知由一组样本数据
的观测值为4.1,则有95%的把握认为两个分类变量有关
C . 已知由一组样本数据 得到的回归直线方程为
得到的回归直线方程为 , 且
, 且 , 则这组样本数据中一定有
, 则这组样本数据中一定有 D . 若随机变量
D . 若随机变量 , 则不论
, 则不论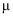 取何值,
取何值, 为定值
为定值
- 目前我国自主研发的抗癌新药西达本胺即将全
- 2009年7月5日晚,乌鲁木齐市发生打砸抢烧严重
- 下列反应的离子方程式不正确的是() A
- 下列各句中,没有语病的―句是 A.学
- 在制作下列食品时,与细菌、真菌无关的是
- 浙江临安钱氏族谱贯穿“念其根、睦其族、尊
- 下列各种物质的用途中,主要利用了其化学性
- 目前“低碳减排”备受关注,CO2的产生及有效
- 在如图所示的电路中,电池的电动势为E,内
- 某兴趣小组为验证日常生活用的火柴头上含有
- 苏丹红是一种人工合成的红色染料.最新研究
- 下列句式与其它三项不同的是( ) A.何
- 若观察到一个动物细胞中正处于染色体两两配
- 今年秋季新学期开学,全国2.2亿中小学生将继
- 下图一架飞机从a城出发途径b岛附近海域后飞
- 下列分子中所有原子不可能共处在同一平面上
- 宇宙飞船运动中需要多次“轨道维持”。所谓
- 下列句子中划线的近义词选用恰当的一项是(
- 下列现象由地球的自转产生( ) A、
- 如图所示,在一直立的光滑管内放置一轻质弹





