回归分析 知识点题库
 =0.577x-0.448,如果某人36岁,那么这个人的脂肪含量( )
=0.577x-0.448,如果某人36岁,那么这个人的脂肪含量( )
 =2.5x+
=2.5x+ , 则某同学每周学习20小时,估计数学成绩约为多少分?
, 则某同学每周学习20小时,估计数学成绩约为多少分?
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)根据上表提供的数据,用最小二乘法求得y关于x的线性回归方程为 =0.7x+a,求a的值;
=0.7x+a,求a的值;
(Ⅲ)请你估计该同学第8年的年收入约是多少?
印刷册数 (千册) | 2 | 3 | 4 | 5 | 8 |
单册成本 (元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:  =
=  ,方程乙:
,方程乙:  =
=  .
.
-
(1) 为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到0.1);
印刷册数x(千册)
2
3
4
5
8
单册成本y(元)
3.2
2.4
2
1.9
1.7
模型甲
估计值

2.4
2.1
1.6
残差

0
﹣0.1
0.1
模型乙
估计值

2.3
2
1.9
残差

0.1
0
0
②分别计算模型甲与模型乙的残差平方和Q1及Q2 , 并通过比较Q1 , Q2的大小,判断哪个模型拟合效果更好.
-
(2) 该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷.根据市场调查,新需求量为8千册(概率0.8)或10千册(概率0.2),若印刷厂以每册5元的价格将书籍出售给订货商,问印刷厂二次印刷8千册还是10千册能获得更多利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本)
年龄x | 21 | 24 | 34 | 41 |
脂肪y | 9.5 | 17.5 | 24.9 | 28.1 |
由表中数据求得y关于x的线性回归方程为  =0.6x
=0.6x  ,若年龄x的值为45,则脂肪含量y的估计值为.
,若年龄x的值为45,则脂肪含量y的估计值为.
 市的普及情况,
市的普及情况,  市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到表格(单位:人).
市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到表格(单位:人).
参考公式:  ,其中
,其中  .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
-
(1) 根据表中数据,能否在犯错误的概率不超过0.15的前提下认为
 市使用网络外卖的情况与性别有关?
市使用网络外卖的情况与性别有关?
-
(2) ①现从所抽取的女网民中利用分层抽样的方法再抽取5人,再从这5人中随机选出了3人赠送外卖优惠券,求选出的3人中至少有2人经常使用网络外卖的概率;
②将频率视为概率,从
 市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为
市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为  ,求
,求  的数学期望和方差.
的数学期望和方差.

参考公式: 
-
(1) 请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
 ,预测记忆力为9的同学的判断力.
,预测记忆力为9的同学的判断力.
-
(2) 若记忆力增加5个单位,预测判断力增加多少个单位?

-
(1) 请利用所给数据求违章人数
 与月份
与月份  之间的回归直线方程
之间的回归直线方程  ,并预测该路口9月份的不“礼让斑马线”违章驾驶员人数;
,并预测该路口9月份的不“礼让斑马线”违章驾驶员人数;
-
(2) 若从表中1月份和4月份的违章驾驶员中,采用分层抽样方法抽取一个容量为7的样本,再从这7人中任选2人进行交规调查,求抽到的两人恰好来自同一月份的概率.
参考公式:
 ,
,  .
.
 (张)与旅游单价
(张)与旅游单价  (元/张)负相关,则其回归方程可能是( )
(元/张)负相关,则其回归方程可能是( ) B .
B .  C .
C .  D .
D . 
y(微克)
 x(千克)
x(千克)
|
|
|
|
|
|
|
3 | 38 | 11 | 10 | 374 | -121 | -751 |
其中 
(I)根据散点图判断,  与
与  ,哪一个适宜作为蔬菜农药残量
,哪一个适宜作为蔬菜农药残量  与用水量
与用水量  的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(Ⅱ)若用解析式  作为蔬菜农药残量
作为蔬菜农药残量  与用水量
与用水量  的回归方程,求出
的回归方程,求出  与
与  的回归方程.(c,d精确到0.1)
的回归方程.(c,d精确到0.1)
(Ⅲ)对于某种残留在蔬菜上的农药,当它的残留量低于20微克时对人体无害,为了放心食用该蔬菜,请估计需要用多少千克的清水清洗一千克蔬菜?(精确到0.1,参考数据  )
)
附:参考公式:回归方程  中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:

| x | | 3 | 4 | | |
| y | | | | 12 | |
对于表中数据,现给出以下拟合曲线,其中拟合程度最好的是 

 B .
B .  C .
C .  D .
D . 
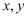 之间是线性相关关系,则由数据表得到的回归直线必过定点( )
之间是线性相关关系,则由数据表得到的回归直线必过定点( ) 
 B .
B .  C .
C .  D .
D . 
 )
B . 若两个具有线性相关关系的变量的相关性越强,则线性相关系数r的值越接近于0
C . 在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高
D . 在线性回归模型中,相关指数R2越接近于1,说明回归的效果越好
)
B . 若两个具有线性相关关系的变量的相关性越强,则线性相关系数r的值越接近于0
C . 在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高
D . 在线性回归模型中,相关指数R2越接近于1,说明回归的效果越好
 进行回归分析,得到一组样本数据:
进行回归分析,得到一组样本数据:  ,则下列说法中不正确的是( )
,则下列说法中不正确的是( )
 必过样本中心
必过样本中心  B . 残差平方和越小的模型,拟合的效果越好
C . 用相关指数
B . 残差平方和越小的模型,拟合的效果越好
C . 用相关指数  来刻画回归效果,
来刻画回归效果,  越小,说明模型的拟合效果越好
D . 若变量
越小,说明模型的拟合效果越好
D . 若变量  之间的相关系数为
之间的相关系数为  ,则变量
,则变量  之间具有线性相关关系
之间具有线性相关关系
 的值判断模型的拟合效果,
的值判断模型的拟合效果,  越大,模型的拟合效果越好;③在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;④若“
越大,模型的拟合效果越好;③在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;④若“  是假命题,
是假命题,  是真命题,则命题p,q一真一假”.其中真命题的个数是( )
是真命题,则命题p,q一真一假”.其中真命题的个数是( )
|
月份 |
1 |
2 |
3 |
4 |
5 |
|
违章驾驶员人数 |
120 |
105 |
100 |
95 |
80 |
-
(1) 请利用所给数据求违章人数
 与月份
与月份  之间的回归直线方程
之间的回归直线方程  ;
;
-
(2) 预测该路口9月份的不“礼让行人”违章驾驶员人数;
-
(3) 交警从这5个月内通过该路口的驾驶员中随机抽查70人,调查驾驶员不“礼让行人”行为与驾龄的关系,得到下表:
不礼让行人
礼让行人
驾龄不超过1年
24
16
驾龄1年以上
16
14
能否据此判断有97.5%的把握认为“礼让行人行为与驾龄有关?
参考公式:
 ,
,  .
. (其中
(其中  )
)P(x2≥k)
0.15
0.10
0.05
0.025
0.010
k
2.072
2.706
3.841
5.024
6.635
①若平面  平面
平面 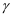 ,平面
,平面  平面
平面 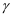 ,则平面
,则平面  平面
平面  ;
;
②“若  ,则
,则  ”的逆否命题为真命题;
”的逆否命题为真命题;
③在线性回归模型中,相关指数  表示解释变量
表示解释变量  对于预报变量
对于预报变量  的贡献率,
的贡献率,  越接近于0,表示回归效果越好;
越接近于0,表示回归效果越好;
④两个模型中残差平方和越小的模型拟合的效果越好;
| 月份x | 2 | 4 | 6 | 8 | 10 |
| 销售金额y(单位:万元) | 64 | 132 | a | 286 | 368 |
若用最小二乘法求得回归直线方程为  ,则
,则  ( )
( )
- — Have you seen my email about our TESL project? — Yes.
- 物体做平抛运动时,从抛出点开始,物体在时
- 某面积较小的岛国为改变淡水供给不足
- 右图是马星驰先生所作的漫画《民气—致之效
- 将2 mol X和2 mol Y充入2 L密闭容器中发生如下反
- Have you heard about Leap year? Leap year is a year that ha
- 李磊在厨房帮妈妈做饭时观察到下列一些现象
- 由于新疆2011年春季较短,伊犁河谷气温回升
- 按要求填表(类别填单质、化合物、氧化物)
- 今年央视“3·15”特别节目曝光,某品牌肉制
- 将氯水分别滴入下列各选项所述的溶液中,由
- 下列关于生物工程中常见的几种酶的叙述,正
- 下图为对流层大气某要素等值面垂直分布图。
- 如图所示,电源电动势E=10V,内阻r=0.5Ω,“8V
- 在化学电源中,转化为电能的是( )A
- 为探究燃烧的条件,某同学查阅资料得知:白
- 下列物质属于酯类的是①豆油 ②甘油 ③牛油
- (12分)材料一:今年是雷锋同志逝世50周年
- 图表资料可以为我们提供很多信息。下面是某
- 下列反应中不属于水解反应的是( ) A.纤维素