回归分析 知识点题库
 =bx+a必过( )
=bx+a必过( )
 ,0)点
C . (0,
,0)点
C . (0, )点
D . (
)点
D . ( ,
, )点
)点
 , 则变量x增加1个单位时( )
, 则变量x增加1个单位时( ) 的值分别为
的值分别为 , 则y关于x的线性回归方程必过点( )
, 则y关于x的线性回归方程必过点( )
①函数关系是一种确定性关系;
②在回归分析中,残差图中的纵坐标为残差;
③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;
④复数﹣1+i的共轭复数是﹣1﹣i.
 ,
,  , …,
, …, 来判断模型拟合的效果,判断原始数据中是否存在可疑数据,这方面的分析工作称为 分析.
来判断模型拟合的效果,判断原始数据中是否存在可疑数据,这方面的分析工作称为 分析.
2015男篮亚锦赛决赛阶段,中国男篮以9连胜的不败战绩赢得第28届亚锦赛冠军,同时拿到亚洲唯一1张直通里约奥运会的入场券.赛后,中国男篮主力易建联荣膺本届亚锦赛MVP(最有价值球员),如表是易建联在这9场比赛中投篮的统计数据.
比分 | 易建联技术统计 | |||
投篮命中 | 罚球命中 | 全场得分 | 真实得分率 | |
中国91﹣42新加坡 | 3/7 | 6/7 | 12 | 59.52% |
中国76﹣73韩国 | 7/13 | 6/8 | 20 | 60.53% |
中国84﹣67约旦 | 12/20 | 2/5 | 26 | 58.56% |
中国75﹣62哈萨克期坦 | 5/7 | 5/5 | 15 | 81.52% |
中国90﹣72黎巴嫩 | 7/11 | 5/5 | 19 | 71.97% |
中国85﹣69卡塔尔 | 4/10 | 4/4 | 13 | 55.27% |
中国104﹣58印度 | 8/12 | 5/5 | 21 | 73.94% |
中国70﹣57伊朗 | 5/10 | 2/4 | 13 | 55.27% |
中国78﹣67菲律宾 | 4/14 | 3/6 | 11 | 33.05% |
注:①表中a/b表示出手b次命中a次;
②TS%(真实得分率)是衡量球员进攻的效率,其计算公式为:
TS%=  .
.

(Ⅰ)从上述9场比赛中随机选择一场,求易建联在该场比赛中TS%超过50%的概率;
(Ⅱ)从上述9场比赛中随机选择两场,求易建联在这两场比赛中TS%至少有一场超过60%的概率;
(Ⅲ)用x来表示易建联某场的得分,用y来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断y与x之间是否具有线性相关关系?结合实际简单说明理由.
 (单位厘米)和身高
(单位厘米)和身高  (单位厘米)的关系,从该班随机抽取10名学生,根据测量数据的散点图可以看出
(单位厘米)的关系,从该班随机抽取10名学生,根据测量数据的散点图可以看出  与
与  之间有线性相关关系,设其回归直线方程为
之间有线性相关关系,设其回归直线方程为  .已知
.已知  ,
,  ,
,  .该班某学生的脚长为24,据此估计其身高为( )
.该班某学生的脚长为24,据此估计其身高为( )
 ,需要研究它和原料有效成分含量
,需要研究它和原料有效成分含量  之间的相关关系,现收集了4组对照数据。
之间的相关关系,现收集了4组对照数据。
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
(Ⅰ)请根据相关系数  的大小判断回收率
的大小判断回收率  与
与  之间是否存在高度线性相关关系;
之间是否存在高度线性相关关系;
(Ⅱ)请根据上表提供的数据,用最小二乘法求出  关于
关于  的线性回归方程
的线性回归方程  ,并预测当
,并预测当  时回收率
时回收率  的值.
的值.
参考数据: 
| 1 | 0 |
|
| 其他 |
| 完全相关 | 不相关 | 高度相关 | 低度相关 | 中度相关 |
 ,
, 
x | 1 | 2 | 3 |
y | 3 | 5.99 | 12.01 |
下列四个函数中,模拟效果最好的为( )
 B .
B .  C .
C .  D .
D . 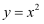

-
(1) 若将被污损的数字视为0-9中10 个数字的随机一个,求北方观众平均人数超过南方观众平均人数的概率.
-
(2) 该节目的播出极大激发了观众学习中国历史知识的热情,现在随机统计了4位观众每周学习中国历史知识的平均时间
 (单位:小时)与年龄
(单位:小时)与年龄  (单位:岁),并制作了对照表(如下表所示):
(单位:岁),并制作了对照表(如下表所示):年龄

20
30
40
50
每周学习中国历史知识平均时间

2.5
3
4
4.5
由表中数据分析,
 呈线性相关关系,试求线性同归方程
呈线性相关关系,试求线性同归方程  ,并预测年龄为60岁观众每周学习中国历史知识的平均时间.
,并预测年龄为60岁观众每周学习中国历史知识的平均时间.参考公式:
 .
.
⑴已知变量  和
和  满足关系
满足关系 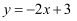 ,则
,则  与
与  正相关;(2)线性回归直线必过点
正相关;(2)线性回归直线必过点  ;(3)对于分类变量
;(3)对于分类变量  与
与  的随机变量
的随机变量  ,
,  越大说明“
越大说明“  与
与  有关系”的可信度越大 (4)在刻画回归模型的拟合效果时,残差平方和越小,相关指数
有关系”的可信度越大 (4)在刻画回归模型的拟合效果时,残差平方和越小,相关指数  的值越大,说明拟合的效果越好.
的值越大,说明拟合的效果越好.
|
时间 |
周一 |
周二 |
周三 |
周四 |
周五 |
周六 |
周日 |
|
车流量(x万辆) |
10 |
9 |
9.5 |
10.5 |
11 |
8 |
8.5 |
|
空气质量指数y |
78 |
76 |
77 |
79 |
80 |
73 |
75 |
-
(1) 根据表中周一到周五的数据,求
 关于
关于  的线性回归方程;
的线性回归方程;
-
(2) 若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2,则认为得到的线性回归方程是可靠的.请根据周六和周日数据,判定所得的线性回归方程是否可靠?
附:回归方程
 中斜率和截距最小二乘估计公式分别为:
中斜率和截距最小二乘估计公式分别为: 其中:
其中: 

 ,
,  ,
,  ,
,  ,下列函数模型中拟合较好的是( )
,下列函数模型中拟合较好的是( )
 B .
B .  C .
C .  D .
D . 
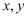 得到一组样本数据,进行回归分析,以下说法正确的是( )
得到一组样本数据,进行回归分析,以下说法正确的是( )
 来刻画回归效果,
来刻画回归效果,  越小说明拟合效果越好;
C . 在回归直线方程
越小说明拟合效果越好;
C . 在回归直线方程  中,当解释变量
中,当解释变量  每增加1个单位时,预报变量
每增加1个单位时,预报变量  平均增加0.2个单位;
D . 若变量
平均增加0.2个单位;
D . 若变量  和
和  之间的相关系数为
之间的相关系数为  ,则变量
,则变量  和
和  之间的负相关很强.
之间的负相关很强.
①由样本数据得到的线性回归方程  必过样本点的中心
必过样本点的中心  ;
;
②由样本点  ,
,  ,…,
,…,  得到回归直线,则这些样本点都在回归直线上;
得到回归直线,则这些样本点都在回归直线上;
③利用  来刻画回归的效果,
来刻画回归的效果,  比
比  的模型回归效果好;
的模型回归效果好;
④残差图中的残差点比较均匀地落在水平的带状区域中,宽度越窄,则说明模型拟合精度越低;
其中正确的结论是( )
 ,
,  ,
,  ,
,  ,
,  ,其频率分布直方图如图1所示.今年某医药研究所研发了一种疫苗,对提高该免疫力有显著效果.经临床检测,将自身免疫力指标比较低的成年人分为五组,各组分别按不同剂量注射疫苗后,其免疫力指标y与疫苗注射量x个单位具有相关关系,样本数据的散点图如图2所示.
,其频率分布直方图如图1所示.今年某医药研究所研发了一种疫苗,对提高该免疫力有显著效果.经临床检测,将自身免疫力指标比较低的成年人分为五组,各组分别按不同剂量注射疫苗后,其免疫力指标y与疫苗注射量x个单位具有相关关系,样本数据的散点图如图2所示. 
附:对于一组样本数据  ,
,  ,…
,…  ,其回归直线
,其回归直线  的斜率和截距的最小二乘估计值分别为
的斜率和截距的最小二乘估计值分别为  ,
,  .
.
-
(1) 设去年七月该医院体检中心共接待5000名成年人体检,试估计这些体检人群中免疫力指标不低于30的人数,并说明理由;
-
(2) 求体检中心抽取的100个人的免疫力指标平均值;
-
(3) 由于大剂量注射疫苗会对身体产生一定的副作用,医学部门设定:自身免疫力指标较低的成年人注射疫苗后,其免疫力指标不应超过普通成年人群自身免疫力指标平均值的3倍.以体检中心抽取的100人作为普通人群的样本,据此估计,疫苗注射量不应超过多少个单位?
 中的L和W具有相关关系
B . 回归直线
中的L和W具有相关关系
B . 回归直线 恒过样本点的中心
恒过样本点的中心 C . 相关系数r的绝对值越接近1,则两个变量的相关性越强
D . 对分类变量x与y的随机变量
C . 相关系数r的绝对值越接近1,则两个变量的相关性越强
D . 对分类变量x与y的随机变量 来说,
来说, 越小,判断“x与y有关系”的把握越大
越小,判断“x与y有关系”的把握越大
- 在生产实践中,利用植物生长素类似物促进扦
- —Look,here comes your dream girl. Invite her to dance.
- 下列关于中国近代“半殖民地半封建社会”的
- S. H. E. is going to sing at the CCTV annual Spring Festiva
- 下列对《晚清政府财政收入结构表》(数额单
- 下列因素中哪个不是诱变剂? A γ射线 B
- 孔子曾提出过“君子和而不同”的思想,意思
- 美国南北战争的导火线是( ) A.奴隶制
- We ______ the difficulty together, but why didn’t you t
- Standing on the top of a church tower not far from our home
- 下列说法正确的是( ) A.形状规则质量分
- 某商场扶梯的高度是5m,扶梯长是7m,小明体
- Elizabeth Clay decided to go home and spend the holiday with
- 若直线y=2x+m-4按向量a=(-1,2)平移后得到的直线
- 下列加点词语使用正确的是() (2分) A
- (Reuters)—A Malaysia Airlines flight carrying 227 pas
- AB是的直径,点C是上一点,连接AC、BC,直线MN
- 室温下,将1.000 mol·L-1盐酸滴入20.00 mL 1.000 mo
- 联合国教科文组织对世界文化与自然遗产的确
- 在平面直角坐标系xOy中,第Ⅰ象限存在沿y轴






