回归分析 知识点题库
①回归方程适用于一切样本和总体。
②回归方程一般都有时间性。
③样本取值的范围会影响回归方程的适用范围。
④回归方程得到的预报值是预报变量的精确值。
 B .
B .  C .
C .  D .
D . 
 =2-x的说法中,不正确的是( )
=2-x的说法中,不正确的是( ) )
C . 当x=l时,y的预报值为l
D . 当残差平方和
)
C . 当x=l时,y的预报值为l
D . 当残差平方和 越小时模型拟合的效果越好
越小时模型拟合的效果越好
给出下列五个命题:
①某班级一共有52名学生,现将该班学生随机编号,用系统抽样的方法抽取一个容量为4的样本,已知7号、33号、46号同学在样本中,那么样本中另一位同学的编号为23;
②一组数据1,2,3,3,4,5的平均数、众数、中位数都相同;
③一组数据为a,0,1,2,3,若该组数据的平均值为1,则样本标准差为2;
④根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为y=a+bx中, 则a=1;
则a=1;
⑤如图是根据抽样检测后得出的产品样本净重(单位:克)数据绘制的频率分布直方图,已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是90.
其中真命题为( )
①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;
②用相关指数 ![]() 来刻画回归效果,
来刻画回归效果, ![]() 的值越大,说明模型的拟合效果越好;
的值越大,说明模型的拟合效果越好;
③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小,拟合效果越好.
其中正确命题的个数是( )

现已求得上表数据的回归方程 =
= x+
x+ 中的
中的 的值为0.9,则据此回归模型可以预测,加工90个零件所需要的加工时间约为( )
的值为0.9,则据此回归模型可以预测,加工90个零件所需要的加工时间约为( )
 =bx+a( b=﹣20,a=
=bx+a( b=﹣20,a= ﹣b
﹣b )的关系,且该产品的成本是4元/件,为使工厂获得最大利润(利润=销售收入﹣成本),该产品的单价应定为( )元.
)的关系,且该产品的成本是4元/件,为使工厂获得最大利润(利润=销售收入﹣成本),该产品的单价应定为( )元.单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
 B . 8
C .
B . 8
C .  D .
D . 
①函数关系是一种确定性关系;
②相关关系是一种非确定性关系;
③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;
④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.
 与
与  的回归模型中,分别选择了
的回归模型中,分别选择了  个不同模型,它们对应的
个不同模型,它们对应的  的值如下,其中拟合效果最好的模型是( )
的值如下,其中拟合效果最好的模型是( )
 对应的
对应的  B . 模型
B . 模型  对应的
对应的  C . 模型
C . 模型  对应的
对应的  D . 模型
D . 模型  对应的
对应的 
 (元)与印刷数
(元)与印刷数  (千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.
(千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.

表中  ,
,  .
.
(附:对于一组数据  ,其回归直线
,其回归直线  的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为  ,
,  )
)
-
(1) 根据散点图判断:
 与
与  哪一个更适宜作为每册成本费
哪一个更适宜作为每册成本费  (元)与印刷数
(元)与印刷数  (千册)的回归方程类型?(只要求给出判断,不必说明理由)
(千册)的回归方程类型?(只要求给出判断,不必说明理由)
-
(2) 根据(1)的判断结果及表中数据,建立
 关于
关于  的回归方程(回归系数的结果精确到0.01);
的回归方程(回归系数的结果精确到0.01);
-
(3) 若每册书定价为10元,则至少应该印刷多少千册才能使销售利润不低于78840元?(假设能够全部售出,结果精确到1)
 与尺寸
与尺寸  之间近似满足关系式
之间近似满足关系式  (
(  为大于0的常数).现随机抽取6件合格产品,测得数据如下:
为大于0的常数).现随机抽取6件合格产品,测得数据如下:
对数据作了初步处理,相关统计位的值如下表:

-
(1) 根据所给数据,求
 关于
关于  的回归方程;
的回归方程;
-
(2) 按照某项指标测定,当产品质量与尺寸的比在区间
 内时为优等品.现从抽取的6件合格产品中再任选3件,记
内时为优等品.现从抽取的6件合格产品中再任选3件,记  为取到优等品的件数,试求随机变量
为取到优等品的件数,试求随机变量  的分布列和期望.
的分布列和期望.附:对于一组数据
 ,其回归直线
,其回归直线  的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为  ,
,  .
.
日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差 | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数 | 22 | 25 | 29 | 26 | 16 | 12 |
该综合实践研究小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
参考数据:  ;
;
 .
.
参考公式:回归直线  ,其中
,其中  .
.
-
(1) 若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出
 关于
关于  的线性回归方程
的线性回归方程  .
.
-
(2) 若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
 中去掉
中去掉  后,下列说法错误的是( )
后,下列说法错误的是( ) 
 变大
C . 相关指数
变大
C . 相关指数  变大
D . 解释变量x与预报变量y的相关性变强
变大
D . 解释变量x与预报变量y的相关性变强
 的说法正确的是( )
的说法正确的是( )
 越接近
越接近  ,表示回归效果越差
B .
,表示回归效果越差
B .  的值越大,说明残差平方和越小
C .
的值越大,说明残差平方和越小
C .  越接近
越接近 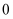 ,表示回归效果越好
D .
,表示回归效果越好
D .  的值越小,说明残差平方和越小
的值越小,说明残差平方和越小
|
零件数x(个) |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
加工时间y(分) |
62 |
68 |
75 |
81 |
89 |
95 |
102 |
108 |
115 |
122 |
-
(1) y与x是否具有线性相关关系?
-
(2) 如果y与x具有线性相关关系,求回归直线方程;
-
(3) 根据求出的回归直线方程,预测加工200个零件所用的时间为多少?
附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线
 =
=  x+
x+  的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为  =
=  ,
,  =
=  -
-  .
.
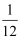 B . 以模型
B . 以模型  去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设  ,将其变换后得到线性方程
,将其变换后得到线性方程  ,则
,则  ,
,  的值分别是
的值分别是  和
和 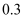 C . 随机变量
C . 随机变量  服从正态分布
服从正态分布  ,
,  ,则
,则  D . 某选手射击三次,每次击中目标的概率均为
D . 某选手射击三次,每次击中目标的概率均为  ,且每次射击都是相互独立的,则该选手至少击中2次的概率为
,且每次射击都是相互独立的,则该选手至少击中2次的概率为 
 和电动自行车驾乘人员交通事故死亡率
和电动自行车驾乘人员交通事故死亡率  ,并整理得到下面的散点图.
,并整理得到下面的散点图. 
参考数据:  ,
,  ,
,  ,
,  .参考公式:相关系数
.参考公式:相关系数  ,回归方程
,回归方程  中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:  ,
,  .
.
-
(1) 求这20个城市的电动自行车头盔佩戴率大于50%的概率;
-
(2) 通过散点图分析
 与
与  的相关关系,说明佩戴安全头盔的必要性;
的相关关系,说明佩戴安全头盔的必要性;
-
(3) 有四名同学通过计算得到
 与
与  的相关系数分别为0.97,0.62,
的相关系数分别为0.97,0.62,  ,
,  ,请你从中选出最有可能正确的结果,并以此求出
,请你从中选出最有可能正确的结果,并以此求出  关于
关于  的线性回归方程.
的线性回归方程.
 拟合比较合适.令
拟合比较合适.令 , 得到
, 得到 , 经计算发现
, 经计算发现 ,
,  满足下表,则
满足下表,则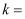 ,
, .
.天数 | 2 | 3 | 4 | 5 | 6 |
| 1.5 | 4.5 | 5.5 | 6.5 | 7 |
- 人生之中,最好的不一定是最合适的,最合适
- 下列物质能在pH=1的溶液中共存且形成无色溶
- 驱蚊草(又名蚊净香草)含有香茅醛,能散发
- 下列命题中正确的是 ( ) A.
- 在下列所述的四种情景中,人对物体做功的是
- 下图所示的岩石分布状态图中,黑色代表的是
- 关于减数分裂的描述,下面哪一种是正确的(
- 下列有关物质制取及性质的叙述正确的是A.
- 一元酯A在酸性条件下水解得到一元饱和羧酸M
- 十五夜望月 (4分)王建中庭地白树栖鸦,
- 如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12
- Are there ______ erasers in the pencil-box?
- 对命题p:“1是集合{x|x2<a}中的元素”,q:“2
- A、B、C、D四种金属,① A+B2+ = B+A2+ ②
- 写作 阅读下面文字,按要求作文。 不管是生
- 有化合物X、Y、Z、W,其焰色反应均为紫色。
- 如图所示,D是一只二极管,它的作用是只允
- 漫画是我们学习历史过程中一种比较生动形象
- 2.下列各句中,没有语病的一句是 A.韩国疾
- 下图是探究绿色植物光合作用速率的实验示意



