分层抽样方法 知识点题库
某林场有树苗30000棵,其中松树苗4000棵.为调查树苗的生长情况,采用分层抽样的方法抽取一个容量为150的样本,则样本中松树苗的数量为( )
A . 30
B . 25
C . 20
D . 15
某中学的高一、高二、高三共有学生1350人,其中高一500人,高三比高二少50人,为了解该校学生健康状况,现采用分层抽样方法进行调查,在抽取的样本中有高一学生120人,则该样本中的高二学生人数为( )
A . 80
B . 96
C . 108
D . 110
某高级中学共有900名学生,现用分层抽样的方法从该校学 生中抽取1个容量为45的样本,其中高一年级抽20人,高三年级抽10人,则该校高二年级学生人数为.
一个单位共有职工  人,其中男职工
人,其中男职工  人,女职工
人,女职工  人.用分层抽样的方法从全体职工中抽取一个容量为
人.用分层抽样的方法从全体职工中抽取一个容量为 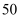 的样本,应抽取女职工人。
的样本,应抽取女职工人。
 人,其中男职工
人,其中男职工  人,女职工
人,女职工  人.用分层抽样的方法从全体职工中抽取一个容量为
人.用分层抽样的方法从全体职工中抽取一个容量为 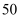 的样本,应抽取女职工人。
的样本,应抽取女职工人。
完成下列两项调查: 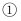 从某社区
从某社区  户高收入家庭、
户高收入家庭、  户中等收入家庭、
户中等收入家庭、  户低收入家庭中选出
户低收入家庭中选出 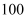 户,调查社会购买能力的某项指标;
户,调查社会购买能力的某项指标;  从某中学的
从某中学的  名艺术特长生中选出
名艺术特长生中选出  名调查学习负担情况.这两项调查宜采用的抽样方法依次是( )
名调查学习负担情况.这两项调查宜采用的抽样方法依次是( )
 从某社区
从某社区  户高收入家庭、
户高收入家庭、  户中等收入家庭、
户中等收入家庭、  户低收入家庭中选出
户低收入家庭中选出 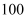 户,调查社会购买能力的某项指标;
户,调查社会购买能力的某项指标;  从某中学的
从某中学的  名艺术特长生中选出
名艺术特长生中选出  名调查学习负担情况.这两项调查宜采用的抽样方法依次是( )
名调查学习负担情况.这两项调查宜采用的抽样方法依次是( )
A .  简单随机抽样,
简单随机抽样,  系统抽样
B .
系统抽样
B .  分层抽样,
分层抽样,  简单随机抽样
C .
简单随机抽样
C .  系统抽样,
系统抽样,  分层抽样
D .
分层抽样
D . 
 都用分层抽样
都用分层抽样
 简单随机抽样,
简单随机抽样,  系统抽样
B .
系统抽样
B .  分层抽样,
分层抽样,  简单随机抽样
C .
简单随机抽样
C .  系统抽样,
系统抽样,  分层抽样
D .
分层抽样
D . 
 都用分层抽样
都用分层抽样
某市政府为减轻汽车尾气对大气的污染,保卫蓝天,鼓励广大市民使用电动交通工具出行,决定为电动车(含电动自行车和电动汽车)免费提供电池检测服务.现从全市已挂牌照的  电动车中随机抽取100辆委托专业机构免费为它们进行电池性能检测,电池性能分为需要更换、尚能使用、较好、良好四个等级,并分成电动自行车和电动汽车两个群体分别进行统计,样本分布如图.
电动车中随机抽取100辆委托专业机构免费为它们进行电池性能检测,电池性能分为需要更换、尚能使用、较好、良好四个等级,并分成电动自行车和电动汽车两个群体分别进行统计,样本分布如图.
 电动车中随机抽取100辆委托专业机构免费为它们进行电池性能检测,电池性能分为需要更换、尚能使用、较好、良好四个等级,并分成电动自行车和电动汽车两个群体分别进行统计,样本分布如图.
电动车中随机抽取100辆委托专业机构免费为它们进行电池性能检测,电池性能分为需要更换、尚能使用、较好、良好四个等级,并分成电动自行车和电动汽车两个群体分别进行统计,样本分布如图. 
-
(1) 采用分层抽样的方法从电池性能较好的电动车中随机抽取9辆,再从这9辆中随机抽取2辆,求至少有一辆为电动汽车的概率;
-
(2) 为进一步提高市民对电动车的使用热情,市政府准备为电动车车主一次性发放补助,标准如下:①电动自行车每辆补助300元;②电动汽车每辆补助500元;③对电池需要更换的电动车每辆额外补助400元.试求抽取的100辆电动车执行此方案的预算;并利用样本估计总体,试估计市政府执行此方案的预算.
“互联网+”时代,全民阅读的内涵已然多元化,倡导读书成为一种生活方式.某校为了解高中学生的阅读情况,从该校1800名高一学生中,采用分层抽样方法抽取一个容量为200的样本进行调查,其中女生有88人.则该校高一男生共有( )
A . 1098人
B . 1008人
C . 1000人
D . 918人
某学校进行体验,现得到所有男生的身高数据,从中随机抽取50人进行统计(已知这50个身高介于  到
到  之间),现将抽取结果按如下方式分成八组:第一组
之间),现将抽取结果按如下方式分成八组:第一组  ,第二组
,第二组  ,
,  ,第八组
,第八组  ,并按此分组绘制如图所示的频率分布直方图,其中第六组
,并按此分组绘制如图所示的频率分布直方图,其中第六组  和第七组
和第七组  还没有绘制完成,已知第一组与第八组人数相同,第六组和第七组人数的比为
还没有绘制完成,已知第一组与第八组人数相同,第六组和第七组人数的比为  .
.
 到
到  之间),现将抽取结果按如下方式分成八组:第一组
之间),现将抽取结果按如下方式分成八组:第一组  ,第二组
,第二组  ,
,  ,第八组
,第八组  ,并按此分组绘制如图所示的频率分布直方图,其中第六组
,并按此分组绘制如图所示的频率分布直方图,其中第六组  和第七组
和第七组  还没有绘制完成,已知第一组与第八组人数相同,第六组和第七组人数的比为
还没有绘制完成,已知第一组与第八组人数相同,第六组和第七组人数的比为  .
. 
(  )补全频率分布直方图;
)补全频率分布直方图;
某电商为了解消费者的下一部手机是否会选购某一品牌手机,随机抽取了200位以前的客户进行调查,得到如下数据:准备购买该品牌手机的男性有80人,不准备买该品牌手机的男性有40人,准备买该品牌手机的女性有40人.
附:  ,
,  .
.
| | 0.50 | 0.25 | 0.05 | 0.025 | 0.010 |
| | 0.455 | 1.321 | 3.840 | 5.024 | 6.635 |
-
(1) 完成下列2×2列联表,并根据列联表判断是否有97.5%的把握认为这200位参与调查者是否准备购买该品牌手机与性别有关.
准备买该品牌手机
不准备买该品牌手机
合计
男性
女性
合计
-
(2) 该电商将这200个样本中准备购买该品牌手机的被调查者按照性别分组,用分层抽样的方法抽取6人,再从这6人中随机抽取3人给予500元优惠券的奖励,另外3人给予200元优惠券的奖励,求获得500元优惠券与获得200元优惠券的被调查者中都有女性的概率.
因新冠疫情的影响,2020年春季开学延迟,老师采用线上教学.某校高中二年级年级组规定:学生每天线上学习时间3小时及以上为合格,3小时以下为不合格.现从1班,2班,3班随机抽取一些学生进行网上学习时间调查,3个班的人数分别为40人,32人,32人,再采用分层抽样的方法从这104人中抽取13人.
-
(1) 应从这3个班中分别抽取多少人?
-
(2) 若抽出的13人中有10人学习时间合格,3人学习时间不合格,现从这13人中随机抽取3人.
(i)设X表示事件“抽取的3人中既有学习时间合格的学生,又有学习时间不合格的学生”,求事件X发生的概率.
(ii)设Y表示抽取的3人中学习时间合格的人数,求随机变量Y的分布列和数学期望.
为了解使用手机是否对学生的学习有影响,某校随机抽取100名学生,对学习成绩和使用手机情况进行了调查,统计数据如表所示(不完整):
|
使用手机 |
不使用手机 |
总计 |
|
|
学习成绩优秀 |
10 |
40 |
|
|
学习成绩一般 |
30 |
||
|
总计 |
100 |
-
(1) 补充完整所给表格,并根据表格数据计算是否有99.9%的把握认为学生的学习成绩与使用手机有关;
-
(2) 现从上表中不使用手机的学生中按学习成绩是否优秀分层抽样选出6人,再从这6人中随机抽取3人,求其中学习成绩优秀的学生恰有2人的概率.
参考公式:
 ,其中
,其中  .
.参考数据:

0.050
0.010
0.001

3.841
6.635
10.828
某饭店共有36名厨师,其中特级厨师6名,一级厨师12名,二级厨师18名.该饭店用分层抽样的方法从这36名厨师中选派  人参加饮食行业的比武大会.但是,即将参加比武大会时,被选出的厨师中恰有一名因病退出,如果再采用系统抽样(等距)方法选派,则选派的人数减少1,且需要从这36名厨师中剔除2人,求
人参加饮食行业的比武大会.但是,即将参加比武大会时,被选出的厨师中恰有一名因病退出,如果再采用系统抽样(等距)方法选派,则选派的人数减少1,且需要从这36名厨师中剔除2人,求  的值.
的值.
 人参加饮食行业的比武大会.但是,即将参加比武大会时,被选出的厨师中恰有一名因病退出,如果再采用系统抽样(等距)方法选派,则选派的人数减少1,且需要从这36名厨师中剔除2人,求
人参加饮食行业的比武大会.但是,即将参加比武大会时,被选出的厨师中恰有一名因病退出,如果再采用系统抽样(等距)方法选派,则选派的人数减少1,且需要从这36名厨师中剔除2人,求  的值.
的值.
在一次跳绳比赛中,35名运动员在一分钟内跳绳个数的茎叶图,如图所示,若将运动员按跳绳个数由少到多编为1~35号,再用系统抽样方法从中抽取7人,把7人跳绳个数由少到多排成一列,第一个人跳绳个数是133,则第5个人跳绳个数是.

2020年4月21日, 总书记向孩子们发出了“文明其精神,野蛮其体魄”的期许,某校为了了解全校学生体育锻炼的情况,随机抽取200名学生进行调查,统计其每天参加锻炼时长(该校学生每天的锻炼时长都落在20~80分钟之间),得到见表:
总书记向孩子们发出了“文明其精神,野蛮其体魄”的期许,某校为了了解全校学生体育锻炼的情况,随机抽取200名学生进行调查,统计其每天参加锻炼时长(该校学生每天的锻炼时长都落在20~80分钟之间),得到见表:
 总书记向孩子们发出了“文明其精神,野蛮其体魄”的期许,某校为了了解全校学生体育锻炼的情况,随机抽取200名学生进行调查,统计其每天参加锻炼时长(该校学生每天的锻炼时长都落在20~80分钟之间),得到见表:
总书记向孩子们发出了“文明其精神,野蛮其体魄”的期许,某校为了了解全校学生体育锻炼的情况,随机抽取200名学生进行调查,统计其每天参加锻炼时长(该校学生每天的锻炼时长都落在20~80分钟之间),得到见表:
|
每天锻炼的时长(分钟) |
| | | | | |
| 人数 | 7 | 12 | 34 | 27 | 80 | 40 |
将每天锻炼时长落在  的学生称为“运动达人”.
的学生称为“运动达人”.
参考公式:  ,其中
,其中  .
.
参考数据:
| | 0.05 | 0.025 | 0.010 |
| | 3.841 | 5.024 | 6.635 |
-
(1) 请根据上述表格的统计数据,填写下面列联表,并根据列联表判断是否有95%的把握认为“运动达人”与性别有关:
运动达人
非运动达人
合计
男生
100
女生
55
合计
200
-
(2) 用分层抽样的方法从“运动达人”中抽取6名学生参加经验分享会,再从中随机抽取2名学生发言.求发言的学生中至少有1名锻炼时长不低于70分钟的概率.
“每天锻炼一小时,健康工作五十年,幸福生活一辈子.”一科研单位为了解员工爱好运动是否与性别有关,从单位随机抽取30名员工进行了同卷调查,得到了如下列联表:
|
男性 |
女性 |
合计 |
|
|
爱好 |
6 |
||
|
不爱好 |
6 |
||
|
合计 |
16 |
30 |
-
(1) 请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程);
-
(2) 能否有95%的把握认为爱好运动与性别有关?
-
(3) 若在接受调查的所有男生中按照“爱好与不爱好运动”进行分层抽样,现随机抽取8人,再从8人中抽取3人,求至少有2人“爱好运动”的概率.
附:


0.05
0.010
0.005

3.841
6.635
7.879
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在  ).
).
 ).
). 
-
(1) 求居民收入在
 的频率;
的频率;
-
(2) 根据频率分布直方图算出样本数据的中位数;
-
(3) 为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10000人中按分层抽样方法抽出100人作进一步分析,则月收入在
 的这段应抽取多少人?
的这段应抽取多少人?
某校为了解学生学习的情况,采用分层抽样的方法从高一2400人、高二20000人、高三 人中,抽取180人进行问卷调查.已知高二被抽取的人数为60人,那么高三被抽取的人数为( )
人中,抽取180人进行问卷调查.已知高二被抽取的人数为60人,那么高三被抽取的人数为( )
 人中,抽取180人进行问卷调查.已知高二被抽取的人数为60人,那么高三被抽取的人数为( )
人中,抽取180人进行问卷调查.已知高二被抽取的人数为60人,那么高三被抽取的人数为( )
A . 72
B . 60
C . 48
D . 84
某高中学校为了促进学生个体的全面发展,针对学生发展要求,开设了富有地方特色的“泥塑”与“剪纸”两个社团,已知报名参加这两个社团的学生共有800人,按照要求每人只能参加一个社团,各年级参加社团的人数情况如下表:
|
高一年级 |
高二年级 |
高三年级 |
|
|
泥塑 |
| | |
| 剪纸 | | | |
其中  ,且“泥塑”社团的人数占两个社团总人数的
,且“泥塑”社团的人数占两个社团总人数的  ,为了了解学生对两个社团活动的满意程度,从中抽取一个50人的样本进行调查,则从高二年级“剪纸”社团的学生中应抽取的人数.
,为了了解学生对两个社团活动的满意程度,从中抽取一个50人的样本进行调查,则从高二年级“剪纸”社团的学生中应抽取的人数.
北京2022年冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”一亮相,好评不断,这是一次中国文化与奥林匹克精神的完美结合,现工厂决定从20只相同的“冰墩墩”,15只相同的“雪容融”和10个相同的北京2022年冬奥会徽章中,采取分层抽样的方法,抽取一个容量为n的样本进行质量检测,若“冰墩墩”抽取4只,则n为( )
A . 8
B . 9
C . 10
D . 12
近日某校组织了一次高二年级数学竞赛,共有 名同学参加了此次竞赛,现将得分情况按
名同学参加了此次竞赛,现将得分情况按 ,
,  ,
,  ,
,  ,
,  ,
,  分组,得到的频率分布直方图如图所示:
分组,得到的频率分布直方图如图所示:
 名同学参加了此次竞赛,现将得分情况按
名同学参加了此次竞赛,现将得分情况按 ,
,  ,
,  ,
,  ,
,  ,
,  分组,得到的频率分布直方图如图所示:
分组,得到的频率分布直方图如图所示:
-
(1) 求频率分布直方图中
 的值,并估计学生成绩的中位数;
的值,并估计学生成绩的中位数;
-
(2) 用分层抽样的方法在区间
 中抽取6人,再从中抽取2名学生的数学成绩,求这2名学生的数学成绩都在区间
中抽取6人,再从中抽取2名学生的数学成绩,求这2名学生的数学成绩都在区间 的概率.
的概率.
最近更新
- 每年高考前后,都有一些学生及家长用敬神、拜佛等迷信方式,祈祷神灵保佑自己或子女金榜题名。对于封建迷信,我们必须坚决予以抵
- ,则f′(﹣2)等于() A.4 B. C.﹣4 D.
- ___ difficult the task may be, we must fulfil it this month.
- 单词拼写 根据下列各句句意及所给单词的首字母或汉语提示,写出所缺单词的正确形式。 1. The theory put f
- 下图为“我国某地某月两日太阳高度日变化示意图”。该月是A.3月 B.6月 C.9月 D.12月
- (08年宁波效实中学期中物理文)空调机、电冰箱和消毒柜都使用了A.温度传感器 B.红外线传感器 C.生物传感
- 如图13-2-4所示,变压器初级线圈接电压一定的交流电,在下列措施中能使电流表示数变小的是( ) A.只将S1
- 我国的根本政治制度是 A.民族区域自治制度 B.社会主义
- 等腰三角形的两边长分别为5和10,则它的周长为 .
- 由同种某物质构成的大小不同的实心物块的体积、质量如下表,以体积V为横坐标,以质量m为纵坐标,在图的方格纸一上描点,再把这
- After investigation, thepolice found out one clue ________
- 罪恶的“三角贸易”的出发点和终点( ) A非洲 B亚洲 C美洲 D
- 下列现象与物质的化学性质无关的是( ) A. 铜丝的导热导电现象 B. 稀硫酸滴入石蕊溶液后溶液变
- 下列自然现象,与太阳辐射无关的是 A.生物的生长 B.大气和水体的运动 C.煤、石油的形成
- 化学方程式是学习化学重要工具之一。写出下列反应的化学方程式并指明反应类型(“化合、分解、氧化”之一): (1)用氢气做燃
- 下列句子中,加横线的词语使用恰当的一项是 A、从新年伊始,中央一再号召各级党组织务真求实,让广大人民的生活安居乐业。 B
- l8.图7为DNA分子结构示意图,下列有关叙述正确的是 ( ) A.若该DNA分子中G—C碱基对比例较高,则
- 设NA为阿伏伽德罗常数的值。下列说法正确的是() A.1.6 g由氧气和臭氧组成的混合物中含有氧原子的数目为0.1N
- 阅读下面三则材料,按要求回答问题。(5分) 材料一 2012年网络流行语大盘点:月光族、围脖、你幸福吗、正能量、切糕、
- I am a good mother to threechildren. I have tried nev













