分层抽样方法知识点题库

某连队身高符合建国60周年国庆阅兵标准的士兵共有45人，其中18岁-19岁的士兵有15人，20岁-22岁的士兵有20人，23岁以上的士兵有10人，若该连队有9个参加阅后的名额，如果按年龄分层选派士兵，那么，该连队年龄在23岁以上的士兵参加阅兵的人数为（）

A . 5 B . 4 C . 3 D . 2

我校高中生共有2700人，其中高一年级900人，高二年级1200人，高三年级600人，现采取分层抽样法抽取容量为135的样本，那么高一、高二、高三各年级抽取的人数分别为( )

A . 45，75，15 B . 45，45，45 C . 30，90，15 D . 45，60，30

某学校高一年级有35个班，每个班的56名同学都是从1到56编的号码，为了交流学习经验，要求每班号码为14的同学留下进行交流，这里运用的是(　　)

A . 分层抽样 B . 抽签抽样 C . 随机抽样 D . 系统抽样

为了了解某工厂开展群众体育活动的情况，拟采用分层抽样的方法从A，B，C三个区中抽取7个工厂进行调查，已知A，B，C区中分别有18，27，18个工厂.

（Ⅰ）求从A，B，C区中分别抽取的工厂个数；

（Ⅱ）若从抽取的7个工厂中随机抽取2个进行调查结果的对比，用列举法计算这2个工厂中至少有1个来自A区的概率．

某校为了解学生学习的情况，采用分层抽样的方法从高一1000人、高二1200人、高三n人中，抽取81人进行问卷调查．已知高二被抽取的人数为30，那么n=（）

A . 860 B . 720 C . 1020 D . 1040

某校一模考试数学测试成绩的茎叶图和频率分布直方图都受到不同程序的破坏，可见部分如下

试根据图表中的信息解答下列问题：

（1）求全班的学生人数及分数在 $\text{[math]}$ 之间的频数；
（2）为快速了解学生的答题情况，老师按分层抽样的方法从位于 $\text{[math]}$ ， $\text{[math]}$ ，和 $\text{[math]}$ 分数段的试卷中抽取8份进行分析，再从中任选2人进行交流，求交流的2名学生中，恰有一名成绩位于 $\text{[math]}$ 分数段的概率.

某班级有50名学生，其中有30名男生和20名女生．随机询问了该班五名男生和五名女生在某次数学测验中的成绩，五名男生的成绩分别为86,94,88,92,90，五名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是( )

A . 这种抽样方法是一种分层抽样 B . 这种抽样方法是一种系统抽样 C . 这五名男生成绩的方差大于这五名女生成绩的方差 D . 该班男生成绩的平均数小于该班女生成绩的平均数

某工厂生产A ， B ， C三种不同型号的产品，产品数量之比依次为2：3：5，现用分层抽样方法抽出一个容量为n的样本，样本中A种型号产品有16件，那么此样本的容量n＝.

某公司有1000名员工，其中：高收入者有50人，中等收入者有150人，低收入者有800人，要对这个公司员工的收入进行调查，欲抽取100名员工，应当采用（）方法

A . 简单呢随机抽样 B . 抽签法 C . 分层抽样 D . 系统抽样

某中学有高中生960人，初中生480人，为了了解学生的身体状况，采用分层抽样的方法，从该校学生中抽取容量为 $\text{[math]}$ 的样本，其中高中生有24人，那么 $\text{[math]}$ 等于（）

A . 12 B . 18 C . 24 D . 36

一支田径队有男运动员 $\text{[math]}$ 人，女运动员 $\text{[math]}$ 人，现按性别用分层抽样的方法从中抽取 $\text{[math]}$ 位运动员进行健康检查，则男运动员应抽取人．

南充高中扎实推进阳光体育运动，积极引导学生走向操场，走进大自然，参加体育锻炼，每天上午第三节课后全校大课间活动时长35分钟．现为了了解学生的体育锻炼时间，采用简单随机抽样法抽取了100名学生，对其平均每日参加体育锻炼的时间（单位：分钟）进行调查，按平均每日体育锻炼时间分组统计如下表：

分组	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
男生人数	2	16	19	18	5	3
女生人数	3	20	10	2	1	1

若将平均每日参加体育锻炼的时间不低于120分钟的学生称为“锻炼达人”.

（1）将频率视为概率，估计我校7000名学生中“锻炼达人”有多少?
（2）从这100名学生的“锻炼达人”中按性别分层抽取5人参加某项体育活动.
①求男生和女生各抽取了多少人；

②若从这5人中随机抽取2人作为组长候选人，求抽取的2人中男生和女生各1人的概率.

2021年，广东省将实施新高考，2018年暑期入学的高一学生是新高考首批考生，新高考不再分文理科，采用 $\text{[math]}$ 模式，其中“3”是指语文、数学、外语；“1”是指在物理和历史中必选一科（且只能选一科）；“2”是指在化学，生物，政治，地理四科中任选两科.为积极推进新高考，某中学将选科分为两个环节，第一环节：学生在物理和历史两科中选择一科；第二环节：学生在化学，生物，政治，地理四科中任选两科.若一个学生两个环节的选科都确定，则称该学生的选考方案确定；否则，称该学生选考方案待确定.该学校为了解高一年级1000名学生选考科目的意向，随机选取50名学生进行了一次调查，这50人第一环节的选考科目都确定，有32人选物理，18人选历史；第二环节的选考科目已确定的有30人，待确定的有20人，具体调查结果如下表：

	选考方案确定情况	化学	生物	政治	地理
物理	选考方案确定的有18人	16	11	5	4
物理	选考方案待确定的有14人	5	5	0	0
历史	选考方案确定的有12人	3	5	4	12
历史	选考方案待确定的有6人	0	0	3	2

（1）估计该学校高一年级选考方案确定的学生中选考政治的学生有多少人？
（2）从选考方案确定的12名历史选考生中随机选出2名学生，设随机变量 $\text{[math]}$ ，求 $\text{[math]}$ 的分布列及数学期望 $\text{[math]}$ .
（3）在选考方案确定的18名物理选考生中，有11名学生选考方案为物理、化学、生物，试问剩余7人中选考方案为物理、政治、地理的人数.（只需写出结果）

《朗读者》是一档文化情感类节目，以个人成长、情感体验、背景故事与传世佳作相结合的方式，选用精美的文字，用最平实的情感读出文字背后的价值，深受人们的喜爱.为了了解人们对该节目的喜爱程度，某调查机构随机调查了A，B两个城市各100名观众，得到下面列联表.

	非常喜爱	喜爱	合计
A城市	60		100
B城市		30
合计			200

附： $\text{[math]}$ 其中（ $\text{[math]}$ ）

$\text{[math]}$	0.15	0.10	0.05	0.025	0.010
$\text{[math]}$	2.072	2.706	3.841	5.024	6.635

（1）完成列联表，并根据以上数据，判断是否有90%的把握认为观众的喜爱程度与所处的城市有关?
（2）现从喜爱的观众中利用分层抽样的方法抽取7人做进一步调查并抽取3人进行奖励，求A，B两城各至少有一人获奖的概率.

某校从参加某次知识竞赛的1000同学中，随机抽取60名同学将其成绩（百分制，均为整数）分成 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 六组后，得到部分频率分布直方图（如图），观察图形中的信息，回答下列问题：

（1）补全频率分布直方图，并估计本次知识竞赛的均分；
（2）如果确定不低于85分的同学进入复赛，问这1000名参赛同学中估计有多少人进人复赛；
（3）若从第一组，第二组和第六组三组学生中分层抽取6人，再从这6人中随机抽取2人，求所抽取的2人成绩之差的绝对值大于20的概率.

已知某工厂生产Ⅰ，Ⅱ，Ⅲ三种型号的螺帽，且这三种型号螺帽的周产量之比为 $\text{[math]}$ ，现在用分层抽样的方法从某周生产的螺帽中抽取若干个进行质量检查，若抽取Ⅲ型号螺帽25个，则这三种型号螺帽共抽取的个数为.

2020年开始，国家逐步推行全新的高考制度．新高考不再分文理科，采用3+3模式，其中语文、数学、外语三科为必考科目，满分各150分，另外考生还要依据想考取的高校及专业的要求，结合自己的兴趣爱好等因素，在政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试（6选3），每科目满分100分．为了应对新高考，某高中从高一年级1000名学生（其中男生550人，女生450人）中，根据性别采用分层抽样的方法从中抽取100名学生进行调查．

附参考公式及数据： $\text{[math]}$ ，其中 $\text{[math]}$

$\text{[math]}$	0.05	0.01
$\text{[math]}$	3.841	6.635

（1）学校计划在高二上学期开设选修中的“物理”和“政治”两个科目，为了了解学生对这两个科目的选课情况，对抽取到的100名学生进行问卷调查（假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目），下表是根据调查结果得到的2×2列联表．请将列联表补充完整，并判断是否有95%的把握认为选择科目与性别有关？说明你的理由；

选择“物理”
选择“政治”
总计
男生
10
女生
30
总计
（2）在（1）的条件下，从选择“政治”的学生中抽取5人，再从这5人中随机抽取2 人，设这2人中男生的人数为 $\text{[math]}$ ，求 $\text{[math]}$ 的分布列及数学期望．

下列叙述中，正确的是（）

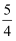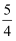A . 某班有40名学生，若采用简单随机抽样从中抽取4人代表木班参加社区活动，那么学号为04的学生被抽到的可能性为40% B . 某大学为了解在校本科生对参加某项社会实践活动的意向，采用分层抽样的方法从该校四个年级的科生中抽取一个容量为500的样木进行调查.已知该校一、二、三、四年级木科生人数之比为 $\text{[math]}$ ，若从四年级中抽取75名学生，则 $\text{[math]}$ C . 四名同学各掷骰子5次，分别记录每次骰子出现的点数，得到四组数据，若某组数据的平均数为2，方差为2.4，则这组数据一定没有出现6 D . 一组数据按从小到大的顺序排列为1，4，4， $\text{[math]}$ ， 7，8（其中 $\text{[math]}$ ），若该组数据的中位数是众数的 $\text{[math]}$ 倍，则该组数据的平均数是6

《中国诗词大会》是央视科教频道推出的一档以“赏中华诗词，寻文化基因，品生活之美”为宗旨的文化类演播室益智竞赛节目，邀请全国各个年龄段、各个领域的诗词爱好者共同参与诗词知识比拼．“百人团”由一百多位来自全国各地的不同年龄段的选手组成，按照年龄分组统计如下表：

分组/岁	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
频数	18	54	36

若用分层抽样的方法从“百人团”中抽取6人参加挑战，则从年龄组 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中抽取的挑战者的人数分别为．

今年上海疫情牵动人心，大量医务人员驰援上海．现从这些医务人员中随机选取了年龄（单位：岁）在 $\text{[math]}$ 内的男、女医务人员各100人，以他们的年龄作为样本，得出女医务人员的年龄频率分布直方图和男医务人员的年龄频数分布表如下：

年龄（单位：岁）	频数
$\text{[math]}$	30
$\text{[math]}$	20
$\text{[math]}$	25
$\text{[math]}$	15
$\text{[math]}$	10

（1）求频率分布直方图中a的值：
（2）在上述样本中用分层抽样的方法从年龄在 $\text{[math]}$ 内的女医务人员中抽取8人，从年龄在 $\text{[math]}$ 内的男医务人员中抽取5人．记这13人中年龄在 $\text{[math]}$ 内的医务人员有m人，再从这m人中随机抽取2人，求这2人是异性的概率：
（3）将上述样本频率视为概率，从所有驰援上海的年龄在 $\text{[math]}$ 内的男医务人员中随机抽取8人，用 $\text{[math]}$ 表示抽到年龄在 $\text{[math]}$ 内的人数，求 $\text{[math]}$ 的数学期望及方差．

	选择“物理”	选择“政治”	总计
男生		10
女生	30
总计

分层抽样方法 知识点题库

分层抽样方法知识点题库