分层抽样方法知识点题库

某全日制大学共有学生5400人，其中专科生有1500人，本科生有3000人，研究生有900人．现采用分层抽样的方法调查学生利用因特网查找学习资料的情况，抽取的样本为180人，则应在专科生、本科生与研究生这三类学生中分别抽取（　　）

A . 55人，80人，45人 B . 40人，100人，40人 C . 60人，60人，60人 D . 50人，100人，30人

某校高三年级共1500人，在某次数学测验后分析学生试卷情况，需从中抽取一个容量为500的样本，按分层抽样，120分以上抽取100人，90～120分抽取250人，则该次测验中90分以下的人数是（　　）

A . 600 B . 450 C . 300 D . 150

某中学高中一年级、二年级、三年级的学生人数比为5：4：3，现要用分层抽样的方法抽取一个容量为240的样本，则所抽取的二年级学生的人数是

某企业有职工450人，其中高级职工45人，中级职工135人，一般职工270人，现抽30人进行分层抽样，则各职称人数分别为（）

A . 5，10，15 B . 3，9，18 C . 3，10，17 D . 5，9，16

某学校有男学生400名，女学生600名，为了解男女学生在学习兴趣与业余爱好方面是否存在显著差异，拟从全体学生中抽取男学生40名，女学生60名进行调查，则这种抽样方法是．

在100个零件中，有一级品20个，二级品30个，三级品50个，从中抽取20个作为样本：①采用随机抽样法，将零件编号为00，01，02，…，99，抽出20个；②采用系统抽样法，将所有零件分成20组，每组5个，然后每组中随机抽取1个；③采用分层抽样法，随机从一级品中抽取4个，二级品中抽取6个，三级品中抽取10个；则（）

A . 不论采取哪种抽样方法，这100个零件中每个被抽到的概率都是 $\text{[math]}$ B . ①②两种抽样方法，这100个零件中每个被抽到的概率都是 $\text{[math]}$ ，③并非如此 C . ①③两种抽样方法，这100个零件中每个被抽到的概率都是 $\text{[math]}$ ，②并非如此 D . 采用不同的抽样方法，这100个零件中每个被抽到的概率各不相同

某校高一年级有男生400人，女生300人，为了调查高一学生对于高二时文理分科的意向，拟随机抽取35人的样本，则应抽取的男生人数为（）

A . 25 B . 20 C . 15 D . 10

每年的12月4日为我国“法制宣传日”.天津市某高中团委在2019年12月4日开展了以“学法、遵法、守法”为主题的学习活动.已知该学校高一、高二、高三的学生人数分别是480人、360人、360人.为检查该学校组织学生学习的效果，现采用分层抽样的方法从该校全体学生中选取10名学生进行问卷测试.具体要求：每位被选中的学生要从10个有关法律、法规的问题中随机抽出4个问题进行作答，所抽取的4个问题全部答对的学生将在全校给予表彰.

（1）求各个年级应选取的学生人数；
（2）若从被选取的10名学生中任选3人，求这3名学生分别来自三个年级的概率；
（3）若被选取的10人中的某学生能答对10道题中的7道题，另外3道题回答不对，记 $\text{[math]}$ 表示该名学生答对问题的个数，求随机变量 $\text{[math]}$ 的分布列及数学期望.

为了响应国家号召，某校组织部分学生参与了“垃圾分类，从我做起”的知识问卷作答，并将学生的作答结果分为“合格”与“不合格”两类与“问卷的结果”有关？

	不合格	合格
男生	14	16
女生	10	20

附： $\text{[math]}$

P（k²≥k）	0.100	0.050	0.010	0.001
$\text{[math]}$	2.703	3.841	6.635	10.828

（1）是否有90%以上的把握认为“性别”与“问卷的结果”有关？
（2）在成绩合格的学生中，利用性别进行分层抽样，共选取9人进行座谈，再从这9人中随机抽取5人发送奖品，记拿到奖品的男生人数为X ，求X的分布列及数学期望 $\text{[math]}$ ．

对一个容量为N的总体抽取容量为n的样本，当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时，总体中每个个体被抽中的概率分别为 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

某车间甲组有10名工人，其中有4名女工人；乙组有5名工人，其中有3名女工人，现采用分层抽样方法（层内采用不放回简单随机抽样）从甲、乙两组中共抽取3名工人进行技术考核.

（I）求从甲、乙两组各抽取的人数；

（II）求从甲组抽取的工人中恰有1名女工人的概率；

（III）记 $\text{[math]}$ 表示抽取的3名工人中男工人数，求 $\text{[math]}$ 的分布列及数学期望.

下列结论正确的有（）

A . 从装有2个红球和2个黑球的口袋内任取2个球，恰有一个黑球与至少有一个红球不是互斥事件 B . 在标准大气压下，水在 $\text{[math]}$ 时结冰为随机事件 C . 若一组数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的众数是 $\text{[math]}$ ，则这组数据的平均数为 $\text{[math]}$ D . 某大学为了解在校本科生对参加某项社会实践活动的意向，拟采用分层抽样的方法从该校四个年级的本科生中抽取一个容量为 $\text{[math]}$ 的样本进行调查.若该校一、二、三、四年级本科生人数之比为 $\text{[math]}$ ，则应从四年级中抽取 $\text{[math]}$ 名学生

某学校参加志愿服务社团的学生中，高一年级有50人，高二年级有30人，高三年级有20人，现用分层抽样的方法从这100名学生中抽取学生组成一个活动小组，已知从高二年级的学生中抽取了6人，则从高三年级的学生中应抽取的人数为（）

A . 2 B . 3 C . 4 D . 5

某校现有高一学生210人，高二学生270人，高三学生300人，用分层抽样的方法从这三个年级的学生中随机抽取n名学生进行问卷调查，如果已知从高一学生中抽取的人数为7，那么从高三学生中抽取的人数应为．

“中华好诗词”河北赛区有40名选手参加初选，测试成绩（单位：分）分组如下：第1组 $\text{[math]}$ ，第2组 $\text{[math]}$ ，第3组 $\text{[math]}$ ，第4组 $\text{[math]}$ ，第5组 $\text{[math]}$ ，得到频率分布直方图如图所示.

（1）求直方图中 $\text{[math]}$ 的值，若90分（含90分）为晋级线，有多少同学晋级？
（2）根据频率分布直方图估计成绩的众数和平均值；
（3）用分层抽样的方法从成绩在第3组到第5组的选手中抽取6名同学组成一个小组，每组中应抽取多少人？

“绿水青山就是金山银山，坚持人与自然和谐共生”的理念越来越深入人心，现已形成了全民自觉参与，造福百姓的良性循环．据此，某网站推出了关于生态文明建设进展情况的调查，调查数据表明，环境治理和保护问题仍是百姓最为关心的热点．现从参与关注生态文明建设的人群中随机选出100人，并将这100人按年龄分为第1组 $\text{[math]}$ ，第2组 $\text{[math]}$ ，第3组 $\text{[math]}$ ，第4组 $\text{[math]}$ ，如图所示，已知区间 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 上的频率依次成等差数列．

（1）分别求出区间 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 上的频率；
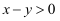（2）现从年龄在 $\text{[math]}$ 及 $\text{[math]}$ 的人群中按分层抽样抽取5人，再从中选3人作为生态文明建设知识宣讲员，用 $\text{[math]}$ 表示抽到作为宣讲员的年龄在 $\text{[math]}$ 的人数， $\text{[math]}$ 表示抽到作为宣讲员的年龄在 $\text{[math]}$ 的人数，求满足 $\text{[math]}$ 的概率．

某校有高一年级学生1000名，高二年级学生1200名，高三年级学生1100名，现用分层抽样的方法从该校所有高中生中抽取330名学生，则抽取的高三年级学生人数为（）

A . 50 B . 70 C . 90 D . 110

第24届冬季奥林匹克运动会（The XXIV Olympic Winter Games），即2022年北京冬季奥运会，是由中国举办的国际性奥林匹克赛事，于2022年2月4日开幕，2月20日闭幕.2022年北京冬季奥运会共设7个大项，15个分项，109个小项．北京赛区承办所有的冰上项目，延庆赛区承办雪车、雪橇及高山滑雪项目，张家口赛区承办除雪车、雪橇、高山滑雪之外的所有雪上项目．为调查学生对冬季奥运会项目的了解情况，某中学进行了一次抽样调查，统计得到以下 $\text{[math]}$ 列联表．

	了解	不了解	合计
男生		60	200
女生	110		200
合计

附： $\text{[math]}$ ．

（1）完成 $\text{[math]}$ 列联表，并判断有超过多大的把握认为该校学生对冬季奥运会项目的了解情况与性别有关；
（2） ①为弄清学生不了解冬季奥运会项目的原因，按照性别采用分层抽样的方法，从样本中不了解冬季奥运会项目的学生中随机抽取5人，再从这5人中抽取3人进行面对面交流，求“男、女生至少各抽到一名”的概率；
②用样本估计总体，若再从该校全体学生中随机抽取40人，记其中对冬季奥运会项目了解的人数为X，求X的数学期望．
附表：
$\text{[math]}$
0.025
0.010
0.005
0.001
$\text{[math]}$
5.024
6.635
7.879
10.828

某高中学校开展学生对宿舍管理员满意度的调查活动，已知该校高一年级有学生1100人，高二年级有学生1000人，高三年级有学生900人.现从全校学生中用分层抽样的方法抽取60人进行调查，则抽取的高一年级学生人数为（）

A . 18 B . 20 C . 22 D . 30

某中学有高中生960人，初中生480人．为了了解学生的身体状况，用比例分配的分层随机抽样方法，从该校学生中抽取容量为 $\text{[math]}$ 的样本，其中高中生有24人，那么 $\text{[math]}$ 等于（）

A . 48 B . 36 C . 24 D . 12

$\text{[math]}$	0.025	0.010	0.005	0.001
$\text{[math]}$	5.024	6.635	7.879	10.828

分层抽样方法 知识点题库

分层抽样方法知识点题库