分层抽样方法 知识点题库

某大学为了解在校本科生对参加某项社会实践活动的意向，拟采用分层抽样的方向，从该校四个年级的本科生中抽取一个容量为300的样本进行调查，已知该校一年级、二年级、三年级、四年级的本科生人数之比为4：5：5：6，则应从一年级本科生中抽取名学生．

为了解城市居民的健康状况，某调查机构从一社区的120名年轻人，80名中年人，60名老年人中，用分层抽样方法抽取了一个容量为n的样本进行调查，其中老年人抽取了3名，则n=（   ）

某校现有高一、高二、高三三个年级共48个教学班，各年级学生数分别是1000，1050，1200，若按分层抽样从全校抽出65名学生，则高二年级比高一年级多抽出名学生．

某高中毕业学年，在高校自主招生期间，把学生的平时成绩按“百分制”折算，排出前n名学生，并对这n名学生按成绩分组，第一组[75，80），第二组[80，85），第三组[85，90），第四组[90，95），第五组[95，100]，如图为频率分布直方图的一部分，其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列，且第四组的人数为60．

（Ⅰ）请在图中补全频率分布直方图；

（Ⅱ）若Q大学决定在成绩高的第3，4，5组中用分层抽样的方法抽取6名学生进行面试．

①若Q大学本次面试中有B、C、D三位考官，规定获得两位考官的认可即面试成功，且面试结果相互独立，已知甲同学已经被抽中，并且通过这三位考官面试的概率依次为 、 ， ，求甲同学面试成功的概率；

②若Q大学决定在这6名学生中随机抽取3名学生接受考官B的面试，第3组中有ξ名学生被考官B面试，求ξ的分布列和数学期望．

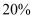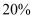我市某小学三年级有甲、乙两个班，其中甲班有男生30人，女生20人，乙班有男生25人，女生25人，现在需要各班按男、女生分层抽取 的学生进行某项调查，则两个班共抽取男生人数是．

省环保厅对 、 、 三个城市同时进行了多天的空气质量监测，测得三个城市空气质量为优或良的数据共有180个，三城市各自空气质量为优或良的数据个数如下表所示：

	城	城	城
优（个）	28
良（个）	32	30

已知在这180个数据中随机抽取一个，恰好抽到记录 城市空气质量为优的数据的概率为0.2.

（I）现按城市用分层抽样的方法，从上述180个数据中抽取30个进行后续分析，求在 城中应抽取的数据的个数；

（II）已知 ， ，求在 城中空气质量为优的天数大于空气质量为良的天数的概率.

某工厂生产A、B、C三种不同型号的产品，产品数量之比依次为k：5：3，现用分层抽样方法抽出一个容量为120的样本，已知A种型号产品共抽取了24件，则C种型号产品抽取的件数为（ ）

调查某校 100 名学生的数学成绩情况，得下表：

	一般	良好	优秀
男生（人）		18
女生（人）	10	17

已知从这批学生中随机抽取1名学生，抽到成绩一般的男生的概率为0.15.

某中学共有360名教师，其中一线教师280名，行政人员55人，后勤人员25人，采取分层抽样，拟抽取一个容量为72的样本，则一线教师应该抽取（    ）人．

某小学、初中、高中一体化学校，学校学生比例如下图，对全校学生采用分层抽样进行一次调查，样本容量为240人，则其中初中女生有（    ）人

某城市的华为手机专卖店对该市市民使用华为手机的情况进行调查.在使用华为手机的用户中，随机抽取100名，按年龄(单位:岁）进行统计的频率分布直方图如图：

某中学有高中生3500人，初中生1500人.为了解学生的学习情况，用分层抽样的方法从该校学生中抽取一个容量为 的样本，已知从高中生中抽取70人，则 为．

某校高一甲、乙两个班分别有男生24名、15名，现用比例分配的分层随机抽样方法从两班男生中抽取样本量为13的样本，对两个班男生的平均身高进行评估．已知甲班、乙班男生身高的样本平均数分别为175cm、177.6cm，以所抽取样本的平均身高作为两个班男生的平均身高，则两个班男生的平均身高为（    ）

现有以下两项调查：①从10台冰箱中抽取3台进行质量检查；②某社区有600户家庭，其中高收入家庭180户，中等收入家庭360户，低收入家庭60户，为了调查家庭购买力的某项指标，拟抽取一个容量为30的样本，则完成这两项调查最适宜采用的抽样方法分别是（    ）

如图是调查某学校高三年级男女学生是否喜欢篮球运动的等高条形图，阴影部分的高表示喜欢该项运动的频率．已知该年级男生女生各500名（假设所有学生都参加了调查），现从所有喜欢篮球运动的同学中按分层抽样的方式抽取32人，则抽取的男生人数为（    ）

某工厂为了解甲､乙两条生产线所生产产品的质量，分别从甲､乙两条生产线生产的产品中各随机抽取了1000件产品，并对所抽取产品的某一质量指数进行检测，根据检测结果按 分组，得到如图所示的频率分布直方图，若该工厂认定产品的质量指数不低于6为优良级产品，产品的质量指数在 内时为优等品.

某种植园在芒果临近成熟时，随机从一些芒果树上摘下100个芒果，其质量分别 ， ， ， ， （单位：克）中，经统计频率分布直方图如图所示．

第24届冬季奥林匹克运动会于2022年2月4日在中国北京开幕，简称“北京冬奥会”．某媒体通过网络随机采访了某市100名关注“北京冬奥会”的市民，其年龄数据绘制成如图所示的频率分布直方图．

2022年，是中国共产主义青年团成立100周年，为引导和带动青少年重温共青团百年光辉历程，某校组织全体学生参加共青团百年历史知识竞赛，现从中随机抽取了100名学生的成绩组成样本，并将得分分成以下6组：[40，50）、[50，60）、[60，70）、、[90，100]，统计结果如图所示：

某中学高一年级有420人，高二年级有460人，高三年级有500人，用分层抽样的方法抽取部分样本，若从高一年级抽取21人，则从高三年级抽取的人数是．