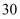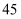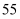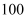分层抽样方法 知识点题库
①一支田径队有男女运动员98人,其中男运动员有56人.按男、女比例用分层抽样的方法,从全体运动员中抽出一个容量为28的样本,那么应抽取女运动员人数是12人;
②采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5,27,38,49的同学均选中,则该班学生的人数为60人;
③废品率x%和每吨生铁成本y(元)之间的回归直线方程为  ,这表明废品率每增加1%,生铁成本大约增加258元;
,这表明废品率每增加1%,生铁成本大约增加258元;
④为了检验某种血清预防感冒的作用,把500名未使用血清和使用血清的人一年中的感冒记录作比较,提出假设H0:“这种血清不能起到预防作用”,利用2×2列联表计算得K2的观测值k≈3.918,经查对临界值表知P(K2≥3.841)≈0.05,由此,得出以下判断:在犯错误的概率不超过0.05的前提下认为“这种血清能起到预防的作用”.
正确的有( )
分组 | 频数 | 频率 |
[10,15) | 12 | 0,10 |
[15,20) | 30 | a |
[20,25) | m | 0.40 |
[25,30) | n | 0.25 |
合计 | 120 | 1.00 |
 ,且该组中,青年人占50%,中年人占40%,老年人占10%. 为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本.试确定:
,且该组中,青年人占50%,中年人占40%,老年人占10%. 为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本.试确定:
-
(1) 游泳组中,青年人、中年人、老年人分别所占的比例;
-
(2) 游泳组中,青年人、中年人、老年人分别应抽取的人数.
-
(1) 求应从这3个协会中分别抽取的运动员的人数.
-
(2) 将抽取的6名运动员进行编号,编号分别为A1 , A2 , A3 , A4 , A5 , A6.现从这6名运动员中随机抽取2人参加双打比赛.
①用所给编号列出所有可能的结果;
②设事件A为“编号为A5和A6的2名运动员中至少有1人被抽到”,求事件A发生的概率.
产品类别 | A | B | C |
产品数量(件) |
| ||
样本容量(件) |
|
由于不小心,表格中A、C产品的有关数据已被污染看不清楚,统计员记得A产品的样本容量比C的样本容量多10,根据以上信息,可得C的产品数量是件.
①命题“  ,有
,有  ”的否定是“
”的否定是“  ,都有
,都有  ”;
”;
②若一个命题的逆命题为真命题,则它的否命题也一定为真命题;
③已知  为假命题,则实数
为假命题,则实数  的取值范围是
的取值范围是  ;
;
④我市某校高一有学生  人,高二有学生
人,高二有学生  人,高三有学生
人,高三有学生  人,现采用分层抽样的方法从该校抽取
人,现采用分层抽样的方法从该校抽取  个学生作为样本进行某项调查,则高三被抽取的学生个数为
个学生作为样本进行某项调查,则高三被抽取的学生个数为  人.
人.
 两个成绩相当的班级,其中
两个成绩相当的班级,其中  班级参与改革,
班级参与改革,  班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过
班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过  分的为进步明显,得到如下列联表.
分的为进步明显,得到如下列联表. | 进步明显 | 进步不明显 | 合计 | |
| | | | |
| | | | |
| 合计 | | | |
-
(1) 是否有
 的把握认为成绩进步是否明显与课堂是否改革有关?
的把握认为成绩进步是否明显与课堂是否改革有关?
-
(2) 按照分层抽样的方式从
 班中进步明显的学生中抽取
班中进步明显的学生中抽取  人做进一步调查,然后从
人做进一步调查,然后从  人中抽
人中抽  人进行座谈,求这
人进行座谈,求这  人来自不同班级的概率.
人来自不同班级的概率. 附:
 ,当
,当  时,有
时,有  的把握说事件
的把握说事件  与
与  有关.
有关.

-
(1) 根据频率分布直方图,估计这50名同学的数学平均成绩;
-
(2) 用分层抽样的方法从成绩低于115的同学中抽取6名,再在抽取的这6名同学中任选2名,求这两名同学数学成绩均在
 中的概率.
中的概率.
 ;方案二:在该地区应用分层抽样的方法抽取30个作为样本区,调查得到样本数据
;方案二:在该地区应用分层抽样的方法抽取30个作为样本区,调查得到样本数据  (
(  ,2,…,30),其中
,2,…,30),其中  和
和  分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得
分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得  ,
,  ,
,  ,
,  ,
,  .
. 附:相关系数  ,
,  ;相关系数
;相关系数  ,则相关性很强,
,则相关性很强,  的值越大,相关性越强.
的值越大,相关性越强.
-
(1) 求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
-
(2) 求方案二抽取的样本
 (
(  ,2,…,30)的相关系数(精确到0.01);并判定哪种抽样方法更能准确的估计.
,2,…,30)的相关系数(精确到0.01);并判定哪种抽样方法更能准确的估计.
 的样本.若样本中90后比00后多52人,则
的样本.若样本中90后比00后多52人,则 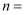 ( )
( ) 
|
年龄段人数类型 |
| | | |
| 使用移动支付 | 45 | 40 | 25 | 15 |
| 不使用移动支付 | 0 | 10 | 20 | 45 |
-
(1) 现从这200人中随机依次抽取2人,已知第1次抽到的人使用移动支付的条件下,求第2次抽到的人不使用移动支付的概率;
-
(2) 在随机抽取的200人中对使用移动支付的人群采用分层抽样的方式抽取25人做进一步的问卷调查再从这25人中随机选出3人颁发参与奖,设这3人中年龄在
 之间的人数为
之间的人数为  ,求
,求  的分布列及数学期望.
的分布列及数学期望.
-
(1) 求从这三个协会中分别抽取的运动员的人数;
-
(2) 将抽取的6名运动员进行编号,编号分别为A1 , A2 , A3 , A4 , A5 , A6 , 现从这6名运动员中随机抽取2人参加双打比赛.
①用所给编号列出所有可能的结果;
②设事件A为“编号为A3和A6的两名运动员中至少有1人被抽到”,求事件A发生的概率.
- 据报载:某地几年前耗资上百万元修建的喷灌工程,由于脱离当地实际几乎成了摆设,当地百姓称之为“废品工程”。这一材料说明(
- (08四川卷)下面照片摄于1945年的一次会议,这次会议的重要内容之一是( ) A.宣布决不再和法西斯国家单独媾
- Ms. Mary was over eighty,but she still drove her old car lik
- “旧时王谢堂前燕,飞入寻常百姓家。”常被用来形容过去的一些昂贵商品现在变成了大众消费品,造成这种变化的主要原因是(
- 血细胞、肌细胞和淋巴细胞所处的内环境分别是 A.血浆、体液、体液 B.血液、体液、淋巴 C.血浆、组织
- 在一定浓度的浓硝酸中加入m克铜镁合金恰好完全溶解(假定硝酸的还原产物只有NO2),向反应后的混合溶液中滴加bmol/LN
- 文艺复兴运动使人们的思想开始从基督教的神学束缚中解放出来。 文艺复时期人文主义者的主要诉求有()①批判神权统治 ②鼓吹人
- 水平传送带匀速运动,速度大小为v,现将一小工件轻轻地放在传送带上,它将在传递带上滑动一段距离后,速度才达到v,而与传送带
- 除去下列物质中的杂质,选用试剂或操作方法不正确是( )物质 所含杂质 除去杂质的试剂或方法 A Na2C03固体
- 如图所示,OB为一轻质杠杆,O为支点,OA=0.3m,OB=0.4m,将重30N的物体悬挂在B点,当杠杆在水平位置平衡
- 为调查某校1600名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况(每人回答最喜欢的一项)并结合调查数据作出如
- 太阳能动力车是利用太阳能电池将接收到的太阳能转化为电能,再利用电动机驱动的一种新型机动车。有一种太阳能实验车(如图所示为
- 某市委书记到基层调研时发现:有的干部下基层征求意见时热热闹闹,解决问题时冷冷清清,甚至把群众当成作秀的道具,群众意见反而
- 仿写题:以某一具体事物(如:大树、小草、灯塔……)开头,仿照例子造句(字数可以不同). 例:小溪是勇敢的,它不畏高山峻岭
- 化简:=__________。
- 能与NaOH溶液、新制Cu(OH)2悬浊液、纯碱溶液、溴水、苯酚钠、甲醇都起反应的是() A.CH3COOH B
- 在古罗马的法律中引用了这样一个案件:在一个公共广场上,一名理发师为一名奴隶刮胡子。另外两个人在附近玩球,其中一个人不小心
- 化学与社会、环境等密切相关。下列说法错误的是() A.“低碳经济”是指减少对化石燃料的依赖,达到低污染、低排放的模式 B
- 人的胰岛细胞能产生胰岛素,但不能产生血红蛋白,据此推测胰岛细胞中( ) A.只有胰岛素基因
- What do they really mean? Food manufacturers and retailers a