已知正四棱锥的底面边长和侧棱长均为，、分别是、上的点，且.

（1）求证：直线∥平面；

（2）求直线与平面所成的角的正切值；

若点O和点F分别为椭圆＋＝1的中心和左焦点，点P为椭圆上的任意一点，则·的最大值为(　　)

A．2       B．3       C．6      D．8

过点P(4，3)，且斜率为的直线的参数方程为(　　)

A． (t为参数)     B.  (t为参数)

C． (t为参数)     D.  (t为参数)

曲线与直线及x轴所围成的封闭图形的面积为　   　．

某市医疗保险实行定点医疗制度，按照“就近就医、方便管理”的原则，参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构，若甲、乙、丙、丁4名参加保险人员所在地区附近有A、B、C三家社区医院，并且他们的选择是相互独立的.

（1）求甲、乙两人都选择A社区医院的概率；

（2）求甲、乙两人不选择同一家社区医院的概率；

（3）设4名参加保险人员中选择A社区医院的人数为ξ，求ξ的分布列和数学期望.

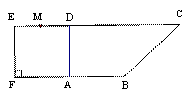
如图1，在直角梯形中，，，且．

现以为一边向形外作正方形，然后沿边将正方形翻折，使平面与平面垂直，为的中点，如图2．

   （1）求证：∥平面；

   （2）求证：平面；

   （3）求点到平面的距离.

            图                                     图

椭圆的焦点在x轴上，焦距为8，则该椭圆的离心率为       ．

如图，在直三棱柱中，已知.设的中点为，

求证：（1）  . 

     ( 2).

已知向量，，且与互相垂直，则的值为      .

将全体正整数排成一个三角形数阵：按照以上排列的规律，第行（）从左向右的第3个数为         

已知椭圆C：和点M（2，1）

（1）求椭圆C的焦点坐标和离心率；

（2）设直线:与椭圆交于两点，求弦长；

（3）求通过M点且被这点平分的弦所在的直线方程．

若，则                。

已知函数=,=.

(Ⅰ)当=2时,求不等式<的解集;

(Ⅱ)设>-1,且当∈[,)时,≤,求的取值范围.

已知函数在其定义域的一个子区间内不是单调函数，则实数的取值范围是（　　）

A.                B.                 C.                  D.

 设展开式中的系数是19，,当展开式中的系数取到最小值时,则展开式中的系数为____ _____。

若不等式2xln x≥－x²＋ax－3对x∈(0，＋∞)恒成立，则实数a的取值范围是    (　  　)

A．(－∞，0)                                       B．(0，＋∞)

C．  (－∞，4]                                     D．[4，＋∞)

是抛物线上一点，是抛物线的焦点，以为始边、为终边的角，则（    ）

已知直线l过点(－1,0)，l与圆C：(x－1)²＋y²＝3相交于A、B两点，则弦长|AB|≥2的

概率为________．

已知在空间四边形OABC中，   点M在OA上，且OM＝3MA，N为BC中点，用a、b、c表示，则等于________.