高二数学试题
从某高中随机选取5名高二男生,其身高和体重的数据如下表所示:
| 身高 x(cm) | 160 | 165 | 170 | 175 | 180 |
| 体重y(kg) | 63 | 66 | 70 | 72 | 74 |
由表可得回归直线方程![]() ,据此模型估计身高为
,据此模型估计身高为![]() 的男生体重大约为
的男生体重大约为
A.70.09 kg B.70.12 kg C.70.55 kg D.71.05 kg
设随机变量,其正态分布密度曲线如图所示,且,那么向正方形OABC中随机投掷20000个点,则落入阴影部分的点的个数的估计值为(附:随机变量![]() ,则
,则![]() )
)
A. ![]() B. 13174 C. 14056 D. 12076
B. 13174 C. 14056 D. 12076

若x,y满足 ,则
,则![]() 的最小值为
的最小值为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
下列结论正确的是( )
A.命题P:![]() >0,都有
>0,都有![]() >0,则
>0,则![]() :
:![]() ≤0,使得
≤0,使得![]() ≤0;
≤0;
B.若命题p和p![]() q都是真命题,则命题q也是真命题;
q都是真命题,则命题q也是真命题;
C.在△ABC中,a,b,c是角A,B,C的对边,则![]() 的充要条件是cosA>cosB;
的充要条件是cosA>cosB;
D.命题“若x2+x-2=0,则x=-2或x=1”的逆否命题是
“x≠-2或x≠1,则x2+x-2≠0”
若变量x,y满足约束条件
 ,则z=x﹣2y的最小值为 .
,则z=x﹣2y的最小值为 .
已知函数![]() (
(![]() 是自然对数底数),方程
是自然对数底数),方程![]() 有四个实数根,则的取值范围为( )
有四个实数根,则的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
在平面直角坐标系中,点![]() 为坐标原点,动点
为坐标原点,动点![]() 与定点F(-1,0)的距离和它到定直线
与定点F(-1,0)的距离和它到定直线![]() 的距离之比是
的距离之比是![]() .
.
(1)求动点P的轨迹![]() 的方程;
的方程;
(2)过![]() 作曲线
作曲线![]() 的不垂直于
的不垂直于![]() 轴的弦
轴的弦![]() ,
,![]() 为
为![]() 的中点,直线
的中点,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
设AB是椭圆![]() (
(![]() )的长轴,若把AB100等分,过每个分点作AB的垂线,交椭圆的上半部分于P1、P2、… 、P99 ,F1为椭圆的左焦点,则
)的长轴,若把AB100等分,过每个分点作AB的垂线,交椭圆的上半部分于P1、P2、… 、P99 ,F1为椭圆的左焦点,则![]() +…
+…![]() 的值是 ( )
的值是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
不论k为何值,直线y=kx+1与焦点在x轴上的椭圆=1恒有公共点,则实数m的取值范围( )。
A.(0,1) B.(0,7) ![]() C. D.
C. D.
已知函数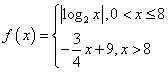 ,若
,若![]() 互不相等,且
互不相等,且![]() ,则
,则![]() 的取值范围是 .
的取值范围是 .
已知方程![]() 所表示的圆有最大的面积,则直线
所表示的圆有最大的面积,则直线![]() 的倾斜角
的倾斜角![]() =_________ .
=_________ .
已知圆![]() 与
与![]() 轴交于0,
轴交于0,![]() 两点,圆
两点,圆![]() 过0,
过0,![]() 两点,且直线
两点,且直线![]() 与圆
与圆![]() 相切;
相切;
(1)求圆![]() 的方程;
的方程;
 (2)若圆
(2)若圆![]() 上一动点
上一动点![]() ,直线
,直线![]() 与圆
与圆![]() 的另一交点为
的另一交点为![]() ,在平面内是否存在定点
,在平面内是否存在定点![]()
![]() 使得
使得![]() 始终成立,若存在求出定点坐标,若不存在,说明理由.
始终成立,若存在求出定点坐标,若不存在,说明理由.
20名学生,任意分成甲、乙两组,每组10人,其中2名学生干部恰好被分在不同组内的概率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
为研究变量![]() 和
和![]() 的线性相关性,甲、乙二人分别作了研究,利用线性回归方法得到回归直线方程
的线性相关性,甲、乙二人分别作了研究,利用线性回归方法得到回归直线方程![]() 和
和![]() ,两人计算知
,两人计算知![]() 相同,
相同,![]() 也相同,下列正确的是( )
也相同,下列正确的是( )
A. ![]() 与
与![]() 重合 B.
重合 B. ![]() 与
与![]() 一定平行
一定平行
C. ![]() 与
与![]() 相交于点
相交于点![]() D. 无法判断
D. 无法判断![]() 和
和![]() 是否相交
是否相交
已知A、B为抛物线E上不同的两点,若以原点为顶点,坐标轴为对称轴的抛物线E的焦点为(1,0),线段AB恰被M(2,1)所平分.
(Ⅰ)求抛物线E的方程;
(Ⅱ)求直线AB的方程.
若椭圆![]() 的离心率为
的离心率为![]() ,则实数
,则实数![]() 的值为 .
的值为 .
设函数f(x)=x(ex-1)-ax2.
(1)若![]() a=,求f(x)的单调区间;
a=,求f(x)的单调区间;
(2)若当x≥0时,f(x)≥0,求a的取值范围
命题“![]() >0,
>0,![]() ≤0”的否定是( )
≤0”的否定是( )
A、![]() >0,
>0,![]() ≤0 B、
≤0 B、![]() >0,
>0,![]() >0
>0
C、![]() >0,
>0,![]() >0 D、
>0 D、![]() ≤0,
≤0,![]() >0
>0
在四棱柱![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是正方形,
是正方形,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,则异面直线
的中点,则异面直线![]() 与
与![]() 所成角的余弦值为_____.
所成角的余弦值为_____.
已知函数![]() ,求:
,求:
(1)函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(2)![]() 的单调递减区间.
的单调递减区间.
- Is this your ring? Please _____ 2356-4859. A. spell B. call
- (14分)X、Y、Z、L、M五种元素的原子序数依次增大。X、Y、Z、L是组成蛋白质的基础元素,M是地壳中含量最高的金属元
- 下列事例中发生的物态变化过程,属于放热的是:A.春天,河里的冰化成水; B.深秋,屋顶的
- 17、已知直四棱柱中,,底面ABCD是直角梯形,A是直角,AB//CD,AB=4,AD=2,DC=1,求异面直线与DC所
- 动植物体内共有的糖是:( ) ①糖元②淀粉③蔗糖④乳糖⑤核糖⑥脱氧核糖⑦葡萄糖⑧果糖 A.②③⑧ B
- 如图所示,光滑水平面上质量分别为mA=2.5 kg、mB=5 kg的两个物体,从静止开始在F=15 N水平外力的作用下经
- (2009北京月考)国务院出台的《医药卫生体制改革近期重点实施方案(2009~2011年)》指出,三年内我国基本医疗保障
- 有金盒、银盒、铅盒各一个,只有一个盒子里有肖像金盒上写有命题p:肖像在这个盒子里;银盒上写有命题q:肖像不在这个盒子里
- 下列溶液一定呈中性的是A.pH=7的溶液 B.c(H+)=c(OH-)=10-6
- .螺旋测微器的读数______厘米;游标卡尺读数_________厘米
- 线粒体上的基因表达产生的酶,与线粒体的功能有关。若线粒体DNA受损伤,则下列过程受影响的有几项
- (已知地球半径为R,地球表面重力加速度为g,不考虑地球自转的影响。(8分) (1)推导第一宇宙速度v1的表达式; (2)
- 有一横截面积为错误!未找到引用源。的铜导线,流经其中的电流为I,设每单位体积导线通过错误!未找到引用源。个自由电子,每个
- CH4—CO2催化重整不仅可以得到合成气(CO和H2),还对温室气体的减排具有重要意义。回答下列问题: (1)CH4—C
- 在江苏卫视《最强大脑》节目中,搭载百度大脑的小度机器人以3:1的总战绩,斩获2017年度脑王巅峰对决的晋级资格,人工智能
- 下图反映了目前不同地区的人口再生产状况,字母分别表示非洲、北美(不包括墨西哥)、亚洲和欧洲,据图回答8~10题:8.图中
- (2分)氧原子的质量数为16,质子数为8,那么它的中子数是____________。
- .下表反映了唐代官市(市署、平准署)官员的设置情况,其职责是直接主持官市的日常管理工作,包括市场交易、物价、度量衡器的管
- 如图,已知 AB // CD,,,求∠1的度数.
- -Is this ________ dictionary? -No, it isn't. It is ________



