高二数学试题
在 ![]() 上定义运算
上定义运算 ![]() ,则满足
,则满足 ![]() 的实数
的实数 ![]() 的取值范围为
的取值范围为 ![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
已知函数![]() ,
,![]()
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)当![]() 时,求证:
时,求证:![]() .
.
曲线y=x3在点(1,1)的切线方程为
设![]() 实数
实数![]() 满足
满足![]() ,其中
,其中![]() .命题
.命题![]() 实数
实数![]() 满足
满足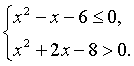
(Ⅰ)若![]() ,且
,且![]() 为真,求实数
为真,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
已知椭圆C的焦点![]() ,长轴长6.
,长轴长6.
(1)求椭圆C的标准方程;
(2)设直线![]() 交椭圆C于A、B两点,求线段AB的中点坐标.
交椭圆C于A、B两点,求线段AB的中点坐标.
已知命题![]() :负数的立方都是负数,命题
:负数的立方都是负数,命题![]() 正数的对数都是负数,则下列命题中是真命题的是
正数的对数都是负数,则下列命题中是真命题的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
已知直线x﹣y+3=0与圆心为(3,4)的圆![]() C相交,截得的弦长为2
C相交,截得的弦长为2![]() .
.
(1)求圆C的方程;
(2)设Q点的坐标为(2,3),且动点M到圆C的切线长与|MQ|的比值为常数k(k>0).若动点M的轨迹是一条直线,试确定相应的k值,并求出该直线的方程.
如图,已知过双曲线![]() 的右顶点
的右顶点![]() 作一个圆,该圆与其渐近线
作一个圆,该圆与其渐近线![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,则该双曲线的离心率为_________.
,则该双曲线的离心率为_________.

某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下表所示:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(h) | 2.5 | 3 | 4 | 4.5 |
(1)求出y关于x的线性回归方程y=bx+a;
(2)试预测加工10个零件需要多少![]() 时间?(温馨提示:
时间?(温馨提示: ![]() =
= ,
, ![]() =
=![]() -
-![]()
![]() .)
.)
如图,在一个60°的二面角的棱上有两个点A,B,AC,BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4,AC=6,BD=8,则CD的长为_________。

在矩形ABCD中,AB=3,AD=4,PA⊥平面ABCD,PA=![]() ,那么二面角A-BD-P的大小为( )
,那么二面角A-BD-P的大小为( )
A.30° B.45° C.60° D.![]() 75°
75°
三位同学独立地做一道数学题,他们做出的概率分别为
![]() 、
、![]() 、
、![]() ,则这三位同学能够将此题解答出的概率为( )。
,则这三位同学能够将此题解答出的概率为( )。
A.0.25 ![]() B.0.5 C.0.6 D.0.75
B.0.5 C.0.6 D.0.75
命题“![]() ,
,![]() ”为真命题的一个充分不必要条件可以是( )
”为真命题的一个充分不必要条件可以是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
某种商品价格与该商品日需求量之间的几组对照数据如下表,经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
| 价格 |
|
|
|
|
|
| 日需求量 |
|
|
|
|
|
(1)根据上表给出的数据,求出![]() 关与
关与![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)利用(1)中的回归方程,当价格![]() 元
元![]() 时,日需求量
时,日需求量![]() 的预测值为多少?
的预测值为多少?
(参考公式:线性回归方程![]() ,其中
,其中 ,
,![]() .)
.)
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
A. ![]() B.
B.![]() C.
C. ![]() 或
或![]() D. 以上答案都不对
D. 以上答案都不对
在等差数列![]() 中,若
中,若![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前n项和,
的前n项和,
(1)求数列的通项公式,(2)n为何值时![]() 最大?并求最大值。
最大?并求最大值。
 如图,在四棱锥P﹣ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,
如图,在四棱锥P﹣ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,
PC=AB=2AD=2CD=2.E是PB的中点.
(1)求证:平面EAC⊥平面PBC;
(2)求二面角P—AC—E的余弦值;
(3)求直线PA与平面EAC所成角的正弦值.
设函数![]() ,则( )
,则( )
A.![]() 为
为![]() 的极大值点 B.
的极大值点 B.![]() 为
为![]() 的极小值点
的极小值点
C.![]() 为
为![]() 的极大值点 D.
的极大值点 D.![]() 为
为![]() 的极小值点
的极小值点
在△ABC中,若![]() ,则
,则![]() 与
与![]() 的大小关系为 ( )
的大小关系为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() ≥
≥![]() D.
D. ![]() 、
、![]() 的大小关系不能确定
的大小关系不能确定
已知![]() 在
在![]() 处取得极值,且
处取得极值,且![]() .
.
(1)求![]() 、
、![]() 的值;
的值;
(2)若对![]() ,
,![]() 恒成立,求的取值范围.
恒成立,求的取值范围.
- 阅读下面的文字,完成12—15题。 要善于应对美国霸权 王逸舟 一位著名中国问题专家分析:“中国与美国关系的重要性体现在
- 若,则为 .
- 我们在探索平面图形性质时,往往通过剪拼的方式帮助我们寻找解题思路.例如,在证明三角形中位线性质定理时,就可以采用下图①的
- 短周期元素M、X、Y、Z,其中X、Y、Z在周期表中所处的位置如图所示.M元素原子的最外层电子数为其次外层电子数的2倍.X
- 下列饮食习惯中,不易患坏血病的是( ) A.生吃新鲜水果
- 下图是西亚一个国家的国旗,国旗上用阿拉伯文写着“万物非主,唯有真主,穆罕默德是安拉的使者。”这表明在这个国家具有特殊地位
- 在实数范围内定义一种运算“*”,其规则为a*b=a2—b2,根据这个规则,求方程(x -2) *1=0的解为______
- The United States is now playing a leading role in the inte
- 短周期元素W、X、Y和Z的原子序数依次增大.W原子是半径最小的原子,非金属元素X形成的一种单质能导电,元素Y是地壳中含量
- The lovely girl is from Class6. ____ name is Alice. A. Her
- 完形填空 I learned how to accept life as it is from
- 在实际生产和生活应用中, 符合力学原理的是( )A.书包带做得较宽, 是为了增大压强;B.菜刀刀刃磨得很锋利,可
- (20分)如图预19-4所示,三个绝热的、容积相同的球状容器A、B、C,用带有阀门K1、K2的绝热细管连通,相邻两球球心
- 下列句子中没有语病的一项是 ( ) A.据科学家统计,蜜蜂每酿
- 已知反应,A、B两物质完全反应时的质量比为3:4,若生成C和D共140g,则该反应消耗B的质量为 A. 60g
- 2007年2月1日,欧洲多国参加了“停电节能5分钟”的活动,借此向浪费能源、破坏环境的行为宣战。这一活动的开展表明
- (10分)有一个小灯泡上标有“4 V 2 W”的字样,现在要用伏安法描绘这个灯泡的U-I图线,有下列器材供选用: A.
- 根据表格中的数据,可以断定方程的一个根所在的区间是( ) -1 0 1 2 30.37 1 2.72 7.39 20
- 读“北半球部分地区某时刻地面等压线图”,回答问题。(1)若A气压中心的形成与地形有关,则该地形可能是
- 设函数f(x)=sin(ωx+φ)(ω>0,-<φ<),给出以下4个论断:①它的图象关于点(,0)对称;②它的图象关于直



